Menger海绵体的斜截面是什么样子的
Menger海绵是三维空间中的经典分形图形，是Sierpinski地毯的三维扩展，最先由数学家Karl Menger提出。它的构造完全仿照Sierpinski地毯的构造方法，只是把平面上的地毯改成了空间中的海绵
【不要错过跑车大奖 - 蒙提霍尔问题】- 有点意思的数学 12
Let's Make a Deal是以前红极一时的电视节目，节目主持人蒙提给你个机会，让你选一扇门，我们把门记为门1，门2，门3。三扇门中之一藏着节目的大奖——一辆红色的跑车，而两扇门后则是山羊，看上去你只有1/3的概率中奖。
幽默感也可以用数学模型量化吗？
阿尔伯塔大学的研究者们为幽默感量身定做了一个数学模型，发现幽默或许不仅仅关乎个人，还与演化和社会信息交流有关。
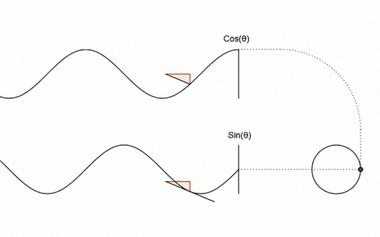
【导数的悖论】- 微积分的本质 02
当你下次再听别人说导数测量的是瞬时变化率，这一自带矛盾的概念的时候，就请自动把它替换成变化率的最佳近似好了。
数学模型教你如何成为星际争霸高手·上篇——确定性模型
本文中，作者用确定性模型告诉大家星际争霸高手的修炼途径。
集数学与艺术于一体的几何幻方
Lee Sallows做了一个网站，收集了很多在几何意义上也成立的幻方，集数学与艺术于一体，为传统意义的幻方赋予了新的生命，大家来欣赏一下吧。
来自圣经的算法
如果还有一本《来自圣经的算法》，哪些算法会列入其中呢？众人在一大堆入围算法中进行投票，最终得出了呼声最高的五个算法。
这些数学原理动图，令人舒心却又伤脑!你看懂几个?
本文介绍一些简单的数学原理，这样的动图你能看懂吗？
如何通俗的解释全微分？
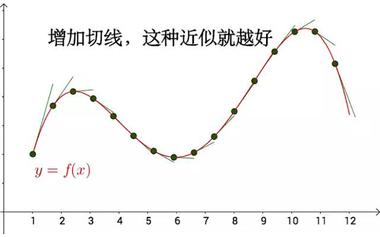
“以直代曲，线性逼近”是整个微积分的精髓，深刻地理解了这八字真言，就会发现微积分一切都很自然了。
关于炉石传说中“傻龙”的数学建模研究
作者使用“状态转移法”建立数学模型分析《炉石传说》游戏中我们应该什么时候用傻龙，傻龙被削之前和之后有什么变化，有多大可能实现极限翻盘。
【秩 / 列空间 / 零空间】- 图解线性代数 09
线性变换后空间的维数，称之为矩阵的秩。换句话说，列空间就是矩阵的列所张成的空间。所以矩阵秩的另一种定义可以说是列空间的维数。经过变换后被压缩到原点的向量集合，称为矩阵A的“零空间”或“核”。
从“迷失的8”到生成函数：小数展开的秘密
事实上，123456789×9=1111111101，偏偏就差一个“1”。而怪就怪在，去掉被除数中的数字“8”，偏偏又有了12345679×9=111111111，一个极其别扭的算式反而得到了完美的结果。