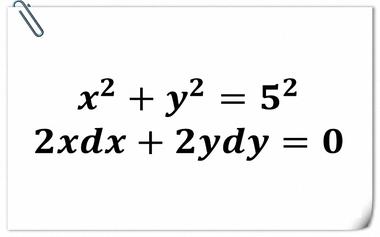为什么Fibonacci数列相邻两项之比会趋于0.618？
Fibonacci数列究竟是怎么和黄金比例扯上关系的？一个简单的解释就是，假设相邻两项之比存在一个极限，那么到了无穷远的时候，连续的三个数a,b,a+b将会满足a/b=b/(a+b)，这正好就是黄金比例的定义。
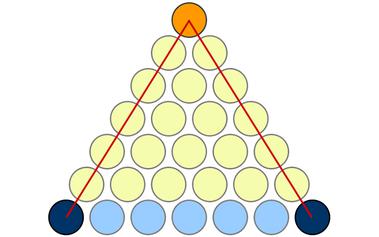
经典证明：1+2+3+…+(n-1) = C(n,2)
本文对1+2+3+…+(n-1) = C(n,2)的证明很奇妙！
【指数函数求导】- 微积分的本质 05
指数函数的一项重要性质就是说，可以将其拆成2^t*2^(dt)。这就能从加法的思想联系到乘法的思想上，比如变化率和比率。
除了正多面体，骰子还可以做成哪些形状？
事实上，对于骰子来说， 正多面体不是必要的。至少不需要那么“正”——只需要满足多面体每个面的地位都相同就可以了。例如，取两个全等的正 n 棱锥，底面和底面互相粘在一起，就能得到一个有 2n 个面的多面体。
一杯咖啡背后的拓扑
从一杯咖啡的搅拌我们可以想象到布劳威尔不动点，从奶泡拉花我们可以观察到曲面自映射的动力学，其背后隐藏的拓扑学原理抽象而凝炼，却又质朴而直观，从中我们可以体会到拓扑学的简洁优美和人类抽象思维的深邃精密。
Lissajous 曲线的动画演示
随着常数m和n的变化，参数方程x=sin(m·t),y=sin(n·t)将会画出一系列漂亮的曲线。法国物理学家Jules Antoine Lissajous曾在1857年研究过这类曲线，因此人们把它叫做Lissajous曲线。
【隐函数求导是怎么回事？】- 微积分的本质 06
x和y是同时有一个等式定义，而相互联系在一起的，这种曲线就是所谓的隐函数曲线。对这种带多个变量的表达式求导，究竟是什么意思？我们为什么要处理如此微小变化量的dy和dx。
这个图形有什么牛B的地方？
对一个正六边形的6个相邻六边形进行黑白二染色，一共可以得到64种构造。
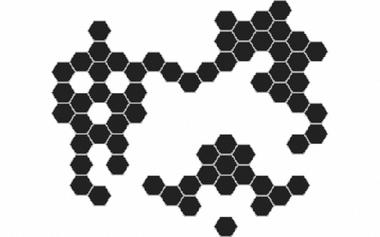
Fibonacci数列转二进制图形的惊异发现
神奇，由前500多位Fibonacci数列的二进制数组成的图的最左下角放大后，想来应该是乱如麻的图形竟然出现了大大小小的直角三角形。
这并不是一个完美的解法，却肯定是你最喜欢的
动态规划的精妙之处在于，每个子问题只求解一次，并将解保存在一个表格中，当需要再次求解此子问题时，只是简单地通过查表获得该子问题的解，避免大量的重复计算。
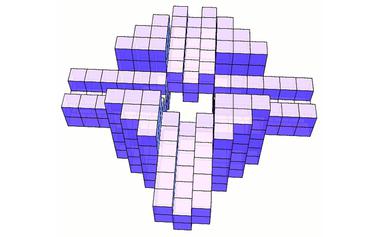
趣题：这个图形有什么独特的性质？
由288个相同的小立方体拼成的一个立体图形，有一个非常独特非常难能可贵的性质。要想用若干个相同的小立方体构造出一个具有同样性质的立体图形，这绝对不是一件容易的事情。
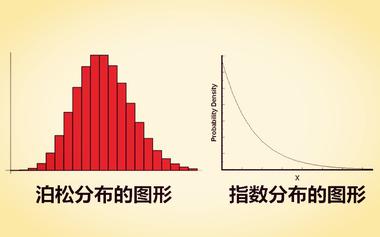
泊松分布和指数分布：10分钟教程
泊松分布是单位时间内独立事件发生次数的概率分布，指数分布是独立事件的时间间隔的概率分布。