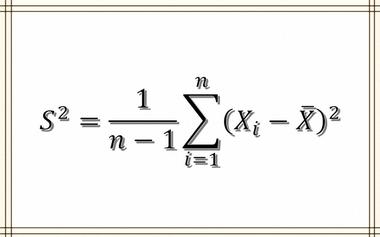一个奇妙的分式方程
Math Horizons 杂志 2010 年 4 月刊上发表了一个有点搞笑的题目，很有些愚人节玩笑的味道。
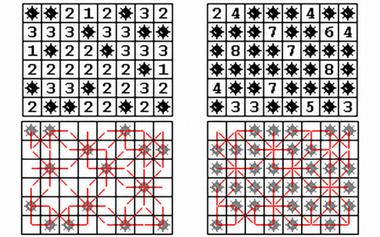
趣题：扫雷定理 互补棋盘上的数字和相等
给定一个扫雷布局，定义它的“补集棋盘”为这样一个新布局，原来有雷的地方现在是空地，原来没有雷的地方现在都是雷。在棋盘的每块空地上都标有一个数字，它表示周围的8个方块中有多少颗雷。一个美妙的结论是，两个互补棋盘布局上的数字和是相等的。
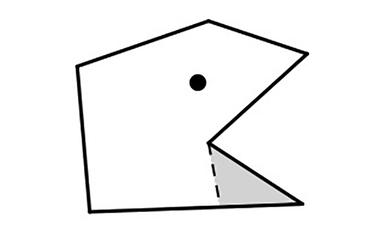
趣题：设计多边形围墙使得对于某一观察点所有的墙都不完全可见
在这个六边形的围墙中，如果站在图中圆点的位置，那么有两面墙不能被完全看见（其中一面墙完全看不见）。能否设计出一个多边形围墙，使得站在围墙里面的某个地方后，所有的墙都至少有一部分是不可见的？
排队怎样排出技术含量？算出还要等多久！
排队实在是一件烦人的事情，但又总是无可避免。排队时我们最想知道的是什么呢？肯定是还要等多久嘛。既然想知道，就把它算出来嘛，反正等着也是等着。
连分数的一个性质以及它的一个组合解释
为什么连分数[a1,a2,a3,…,an]和[an,…,a3,a2,a1]的分子是相同的呢？因为这两个连分数的分子表示的是两个左右镜像的棋盘的砖块放置方案数，而两个左右镜像的棋盘本质上是相同的，它们的砖块放置方案数显然应该相等。
趣题：如果每次只增加一个区域的话
著名的四色定理告诉我们，如果一个地图由若干个连通区域构成（没有飞地），那么在给每个区域染色时为了让相邻区域的颜色不同，最多只需要四种颜色就足够了。不过，这个结论成立有一个条件：整个地图已经事先确定了。如果我们每次只增加一个区域的话呢？
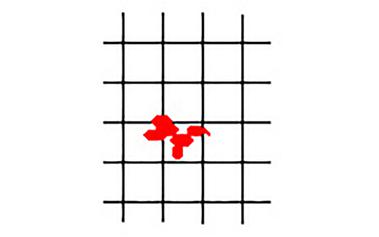
非常奇妙的证明：图形必在格点之外
问题：设想一个平面上布满间距为1的横纵直线，形成由一个个1×1正方形组成的网格。任意给一个面积小于1个单位的图形，证明这个图形总能放在网格中而不包含任何一个格点。
趣题：能否把三维空间分成无穷个圆？
这是一个非常经典的问题：是否存在无穷个互不相交的圆，它们并在一起就是整个三维空间？换句话说，能否用圆形既无重复又无遗漏地填满整个三维空间？
趣题：货架上的听装可乐
有个放听装可乐的货架，它的宽度要比四听可乐的直径稍微大一些。把10听可乐放进这个货架里，堆叠成一个三角形。虽然底下三层可乐罐歪歪斜斜有高有低，但最顶上的那听可乐一定位于货架的正中心，也就是说它到货架两壁的距离是相等的。这是为什么呢？
智猪博弈简介
智猪博弈在社会领域的应用十分广泛，例如市场竞争中的大企业与中小企业、公共服务分配领域中社会全体和社会弱势群体，企业内部分配时的管理者与劳动者等，总之，智猪博弈具有广阔的应用前景和很高的应用价值。
令人敬畏的十维空间
到了十维空间后，中心球的直径将超过十维立方体的边长，这个中心球将突破立方体的边界！被围在里面的中心球居然比原来的N维立方体还大，这显然违反了大多数人的直觉；如果你能想象出这个画面来，你就牛B了。科幻小说中把对十维空间的感知能力作为文明发达程
为什么样本方差的分母是 n-1？
学完概率论还是不知道为什么样本方差的分母是 n-1？没关系，看完这篇文章你就懂了。