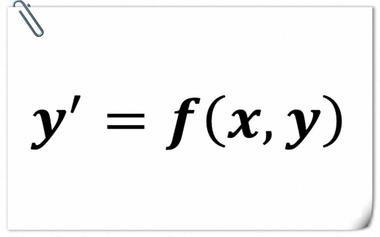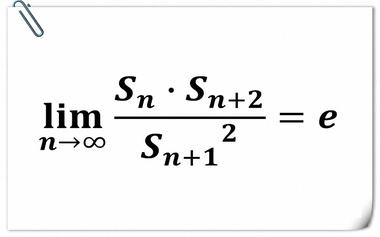- 为您找到相关结果387个
趣题:每个小点最后都会回到自己原来的位置上吗?
熟悉群论的朋友会很快发现,这个结论几乎是显然的。小点的每一步运动都形成了一个置换,三个置换的复合本质上也还是一个置换,而这个置换的足够多次幂一定会变成单位置换。这意味着,不但每个点都能回到自己原来的位置,而且所有点能同时回到自己原来的位置。
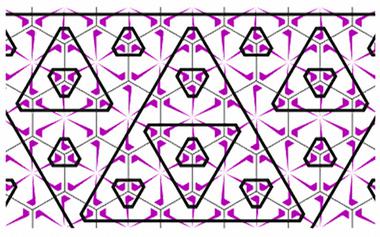
能平铺平面,却不能周期性地平铺平面
虽然正方形、长方形、正六边形等图形都能平铺整个平面,但平铺的方式却非常无聊,不过是同一种模式不断重复罢了。有没有什么“非平凡”的平铺方案呢?本文就给大家看这样一个图形。
如何理解常微分方程的通解、特解以及所有解?
求解常微分方程是有明确的几何意义的。本文通过常微分方程的几何意义,来观察什么是它的通解、特解以及所有解。
趣题:以无理点为圆心的圆周上最多有多少个有理点?
在平面直角坐标系内,任意一个以有理点为圆心,有理数为半径的圆周上总存在无穷多个有理点。那么如果一个圆的圆心是无理点(两个坐标中至少有一个不是有理数),那么圆周上的有理点个数还可能是无穷多个吗?
趣题:能否在等边三角形点阵中画一个正方形?
能否在一个无限大的等边三角形点阵中选取四个点,使得这四个点恰好构成一个正方形?这个问题有一个非常简单巧妙的解法,你能想到吗?
怎样把一个立方体分成 54 个小立方体?
事实上,对于所有的正整数n≥48,把一个立方体分割成n个小立方体都是有可能的。
有心之函数必然就有分手函数
哈哈,这次成功了,裂开的心形!我原创的“分手方程”就此出炉了: 17 x^2 – 16|x|y + 17 y^2 + 150/|5 x + sin(5 y)| < 225 。
神奇的分形艺术(二):一条连续的曲线可以填满整个平面
如何构造一条曲线使得它可以填满整个平面。在这里我们仅仅说明存在一条填满单位正方形的曲线就够了,因为将此单位正方形平铺在平面上就可以得到填满整个平面的曲线。
让你看到函数图象在无穷远处的样子
当x从-π/2连续地增加到π/2时,x的正切值将会从负无穷连续地增加到正无穷。因此,为了展示出y=f(x)在无穷远处的样子,我们可以画出tan(y)=f(tan(x))在(-π/2,π/2)×(-π/2,π/2)上的图象。
玩转内接多边形(二):任意多边形内均存在内接矩形
是否任意一个多边形内都能找到内接矩形呢?答案也是肯定的。本文对它的证明真可谓是巧妙到了诡异的地步,真不知是谁想出来的。
用相同形状的多联骨牌拼接完全对称图形
用相同形状的多联骨牌拼成完全对称图形,问对于哪些多联骨牌问题是有解的。令人吃惊的是,所有不超过6联的骨牌都是有解的。
杨辉三角中的自然底数 e
2012年,Harlan Brothers发现了杨辉三角中的一个有趣的事实。不妨把杨辉三角第n行的所有数之积记作sn,那么随着n的增加,sn·sn+2/sn+12会越来越接近e≈2.718。