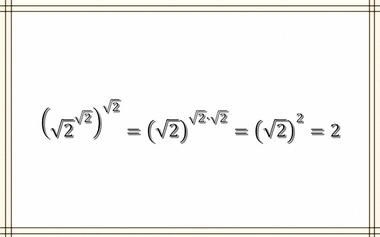Pick定理的几个出人意料的应用
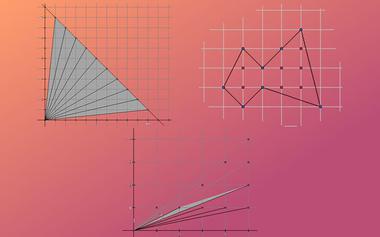
Pick定理是说，在一个平面直角坐标系内，如果一个多边形的顶点全都在格点上，那么这个图形的面积恰好就等于边界上经过的格点数的一半加上内部所含格点数再减一。
无限小却无限大的集合 & 阶梯状的连续函数
它是无穷多个横线段组成的一个连续函数，除端点无意义以外导数值都是0。或者说，这个函数在不变之中上升。
经典证明：几乎所有有理数都是无理数的无理数次方
一个无理数的无理数次方是否有可能是一个有理数？这是一个非常经典的老问题了。答案是肯定的，证明方法非常巧妙。
满足xy恰有k个约数的(x,y)所组成的图形
研究本文中的图像各种有趣的模式产生的原因，无疑是一个有趣的课题。
为什么圆是360度？超颠覆的解释
圆为什么有360度？为什么不是300度呢？我们把圆分成等份，奇迹出现了……
整数分拆中的一个出人意料的结论
事实上，对于任意一个正整数来说，各个分拆方案中不同的数的个数之和一定都等于所有方案中1出现的总次数。这是为什么呢？这个结论还有一个比较直接的推广，你能想到吗？
趣题：竞技场里的狮子能否保证抓住最高速度相同的小明？
小明和狮子同被关在一个半径为 10 米的竞技场里，狮子位于竞技场的圆心处，小明则在距离圆心 1 米的地方。两者的最大运动速度都是每秒 1 米。狮子有没有什么必胜策略，使得不管小明怎么跑，它总能在有限的时间里抓住小明？
UyHiP趣题：限制最苛刻的选票统计程序
为了支持新的民主政策，你需要设计一套算法，来计算每届代表选举大会结束后，哪些公民成为了代表，他们手中各自有多少票的权力。
用一张日落照片估算出地球的半径
Princeton 大学的 Robert Vanderbei 在他的一篇论文中对一张摄于密歇根湖的日落照片进行了分析，不但证实了地球是圆的，还依据照片上的内容对地球半径进行了估算。
图表的重要性：Anscombe的四组数据
1973年，统计学家F.J. Anscombe构造出了四组奇特的数据。它告诉人们，在分析数据之前，描绘数据所对应的图像有多么的重要。
如何理解傅立叶级数、傅立叶变换公式？
本文对傅立叶级数、傅立叶变换公式进行细节的、代数上的解释。
复数的物理意义
引入复数的一个很“物理”的原因是因为对称性。大家最早在物理中接触复数，基本都是在简谐振动那部分。