通过拓扑学分析，科学家探究树叶形状的本质
Chitwood是密苏里州圣路易斯Donald Danforth植物科学中心的前科学家，他的团队使用了一种叫做持续同调的拓扑学算法分析树叶形状。
出租车几何学：一个全新的几何世界
在理想模型中，假设每条道路都是水平或者竖直的，那么只要你朝着目标走（不故意绕远路），不管你怎样走，花费的路程都是一样的。今天，我看到了一个非常有意思的名词——出租车几何学，其名称就来源于这样的想法。
探秘数字8，你会发现数的神奇与美妙
八谐音“发”，是个人见人爱的幸运数字，不管是手机号还是车牌号，谁都想要里面有个数字8。死理性派自然而然地想到一个问题：在全体自然数中，含有数字8的数占多大的比例？10%？50%？还是90%？
五个有趣的拓扑变换问题
如果你喜欢上次的空间想象能力挑战，你一定会喜欢V.V.Prasolov的Intuitive Topology一书。书中的第一章有五个非常经典的“拓扑变换”类谜题，在此与大家分享。
Arrow不可能性定理：独裁是唯一完美的选举制度
同时满足全体一致性、无关候选人独立性（就是那两个基本条件）以及非独裁性这三个条件的选举制度理论上是不存在的。这就是美国经济学家Kenneth Arrow提出的Arrow不可能性定理：不存在完美的选举制度。
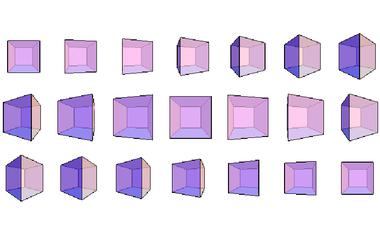
不同维度的对话：带你进入四维世界
如果你以前从来没细想过四维空间的话，相信看了这篇文章后你会有一种超凡脱俗的感觉。
100个囚犯和灯泡的那些事儿（下）
整个问题的唯一解法就是，其中一个人只负责关灯，另外所有人只负责开灯；或者其中一个人只负责开灯，另外所有人都只关灯。换句话说，我们的“统计者协议”其实是唯一的解法。
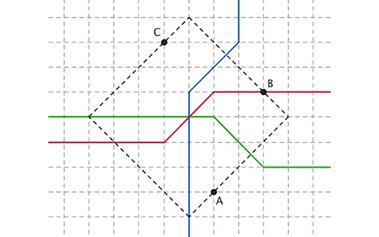
4个最省钱的拼车方案
很多时候拼车人虽然顺路（这是拼车的基础条件），但目的地却不相同。所以自然而然的就会产生一个问题：每个人应该各付多少车费？
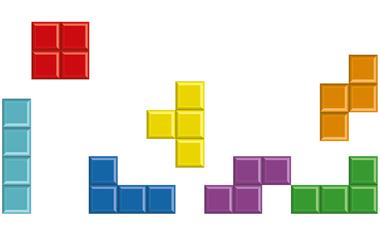
俄罗斯方块可以永无止境地玩下去吗？
俄罗斯方块真的不可能玩死吗？1988年，John Brzustowski的一篇论文指出，俄罗斯方块游戏无解并非不可能。它给出了一种算法可以保证游戏机能够害死玩家，即使我们要求它必须提前向玩家展示出下一个方块的形状。
神奇的分形艺术（四）：Julia集和Mandelbrot集
考虑复数函数f(z)=z^2+c，不同的复数c对应着不同的Julia集。也就是说，每取一个不同的c你都能得到一个不同的Julia集分形图形，并且令人吃惊的是每一个分形图形都是那么美丽。Mandelbrot集的神奇之处就在于，你可以对这个分形
主题公园投资扩建新项目回报分析
2014年-2015年，我国主题公园行业经历了量与质的快速攀升。每年有两位数的主题公园开业，每隔段时间就有国际主题公园宣布进入中国市场。处在2016年的这个时候，各家都在想方设法不让自己被市场淘汰，有的强化市场营销，有的提升服务细节、有的提
神奇的分形艺术（三）：Sierpinski三角形
如果你以前就对Sierpinski三角形有一些了解，这篇文章带给你的震撼将更大，因为你会发现Sierpinski三角形竟然还有这些用途。