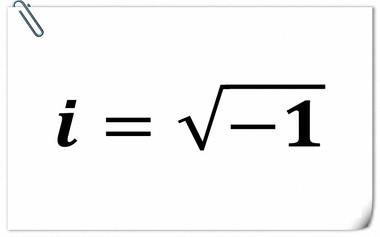Cramer悖论：线性代数的萌芽
虽说数学悖论大多是些让人越想越糊涂的逻辑思维游戏，但也有不少悖论来自实实在在的数学问题。那些最难解决的悖论甚至为数学新分支的开创带来了足够的动机，Cramer悖论就是一个漂亮的例子。
视频 | 【PBS无尽数学】概率——一项随机相关的超级任务
在数学的世界中，你怎么能在有限的时间里来完成无穷多项任务呢？答案是：通过完成“超级任务”。
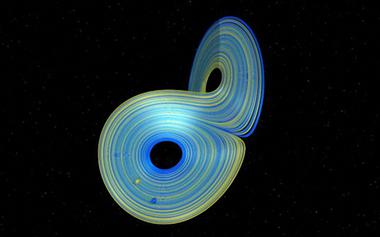
视频合集 | 混沌：数学冒险
还记得前些天给大家介绍的那部精彩却很难懂的《维度：数学漫步》吗？原班人马之后制作了第二季的视频《混沌：数学冒险》，依旧通过生动的动画，为我们介绍了公共动力系统，蝴蝶效应和混沌理论。
代数、几何、分析 各自的范畴
本文简要介绍数学三大核心领域中十几门主要分支学科的有关历史发展情况。
分形图展现了不可抗拒的数学之美
自然中，许多相关的分形会产生漂亮的令人感兴趣的图形。实际上，一些今天被认为是分形的外形早在许多年之前就已发现。
如何打破实数的框框，引入新的虚数
本文从对四则运算闭合的原则出发，展现了从自然数扩大到实数，进而扩大到复数的思维历程。
视频 | 国际象棋的“骑士”与马尔科夫链
国际象棋中如果一个骑士（马）经过随机移动，最后又返回到初始的位置。可能两步就能返回，也可能骑士需要很长时间才找到“回家”的路，那么问题是究竟要平均要跳多少次呢？
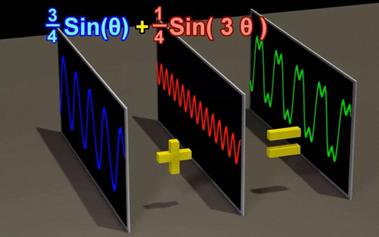
视频 | 傅里叶级数与傅里叶变换
我们在生活中所见到的所有信号都可以看作是无限个正弦波之和，它们从时间长河的开始就已经存在，并且将延伸至永恒。
【史前数学 01】- 数学进化史
数学是人类智慧的结晶，在万年之后，我们再來回首与之相关的一个一个重要时刻，畅游在这时空之中，与各位大师相遇相识，惊叹数学在人类文明发展中都有些什麼让人惊叹的瞬间！
用数学的语言看世界
只要能够证明辛普森有家庭暴力，他杀害布朗的概率为90%。提出这个概率的话，想必就不能“排除合理怀疑”了，所以这显然是一个重要的证据。90%的概率也足以用来反驳德肖维茨教授的主张，这就是数学的力量。
麻省理工(MIT)牛人解说数学体系
麻省理工(MIT)牛人林达华对现代数学体系的解读——以集合论为基础，结合分析和代数，发展到今天的现代概率论。
用事实告诉你高斯有多牛B
高斯作为当之无愧的第一大数学家，他有很多鲜为人知的传奇经历，现在就为你一一八卦。