摘要:本文介绍一些简单的数学原理,这样的动图你能看懂吗?
一、被简单证明的勾股定理
给三角形加上一点厚度,从面积问题,跳转到了具象的体积问题。
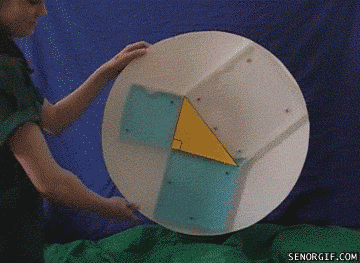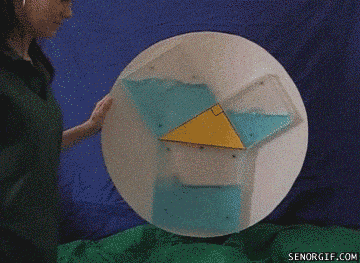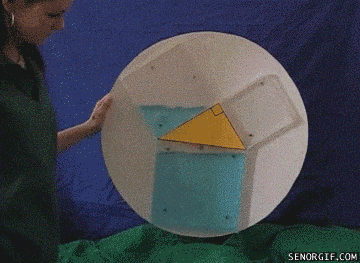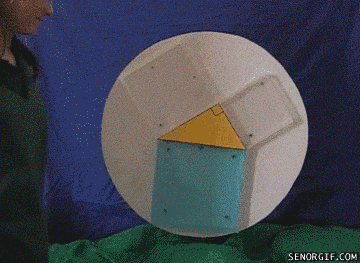
图1
二、勾股定理的面积证明法
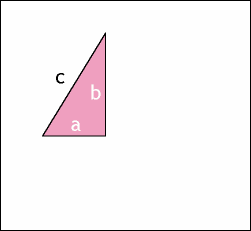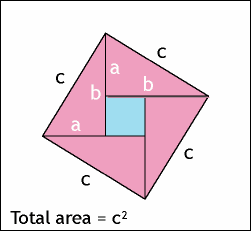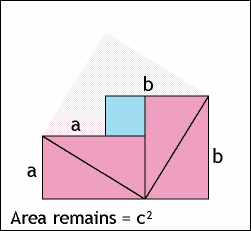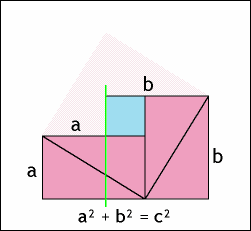
图2
三、周长和直径的π点小事
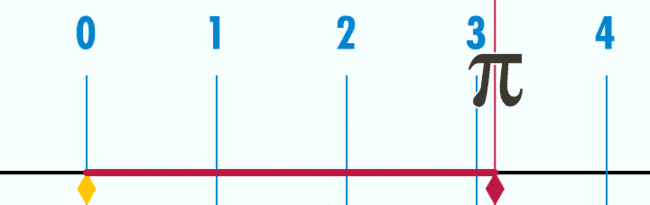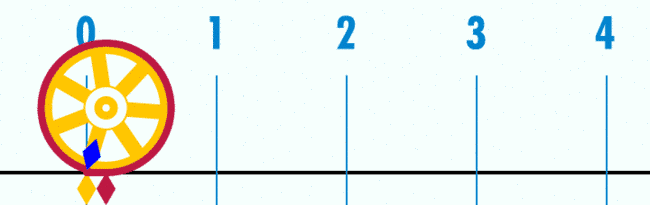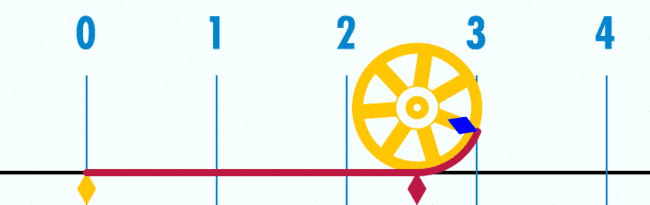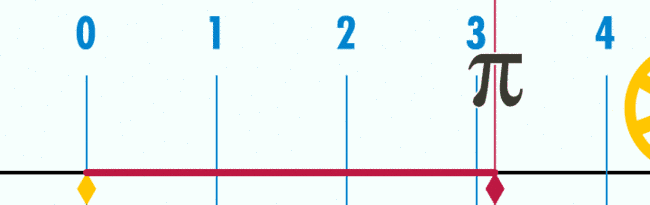
图3
四、圆的面积=2πr?
首先,把圆解剖为一个三角形,底边是周长,然后根据三角形的面积推出圆的面积。

图4
五、一弧度就是长度刚好等于半径的一段圆弧所对的圆心角

图5
六、正切值曲线
这是一个正切线被θ牢牢控制,一辈子都逃不出其手掌心的故事。
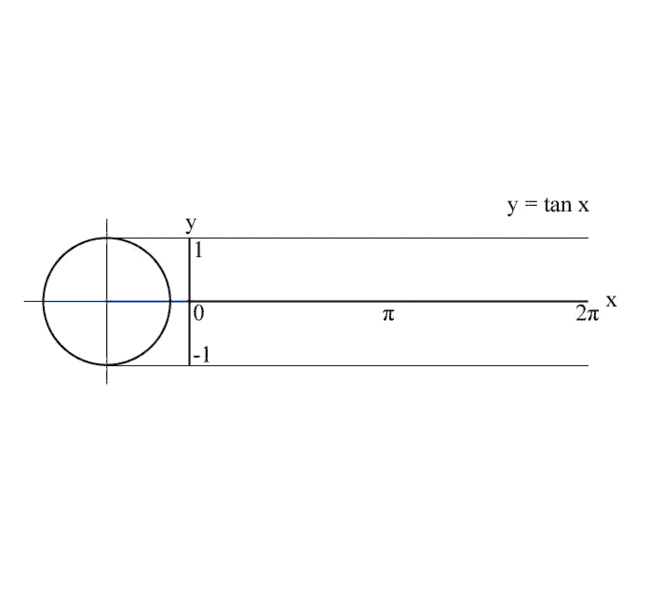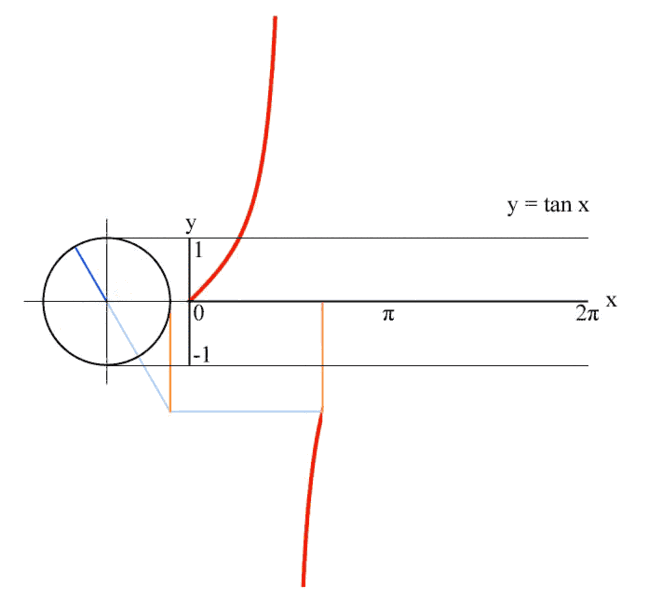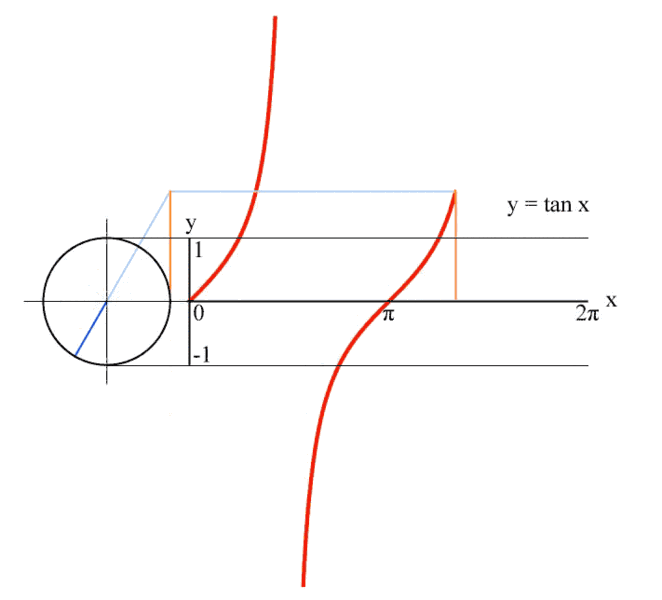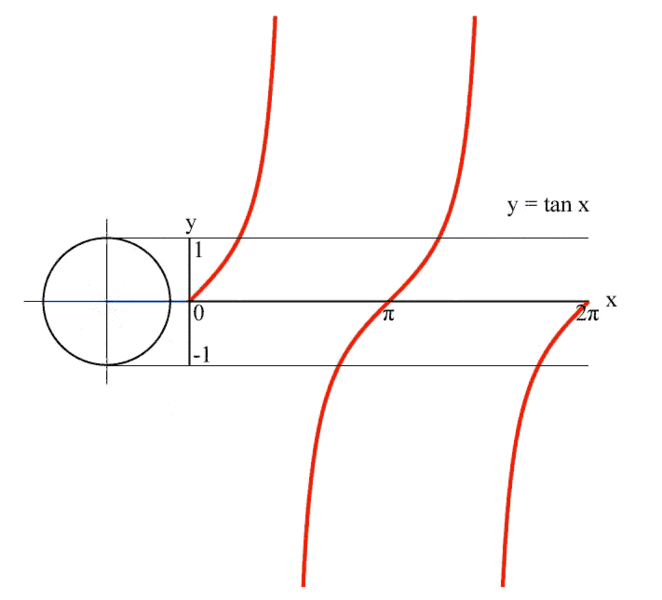
图6
七、看懂上面那个,就不解释这个了
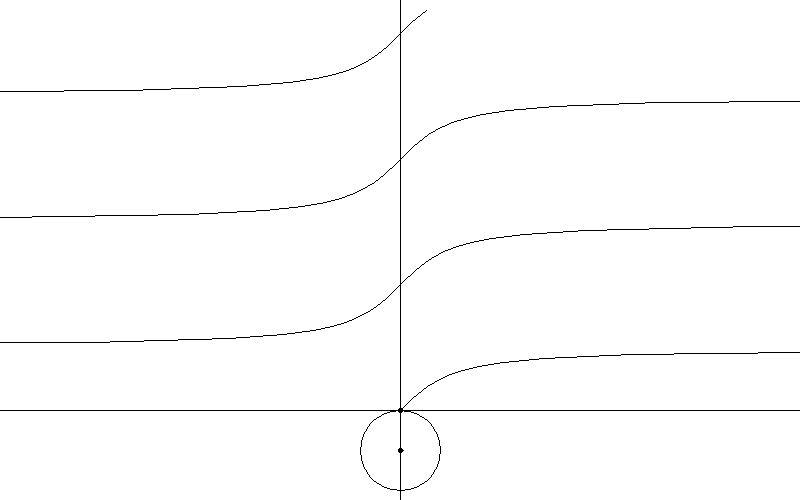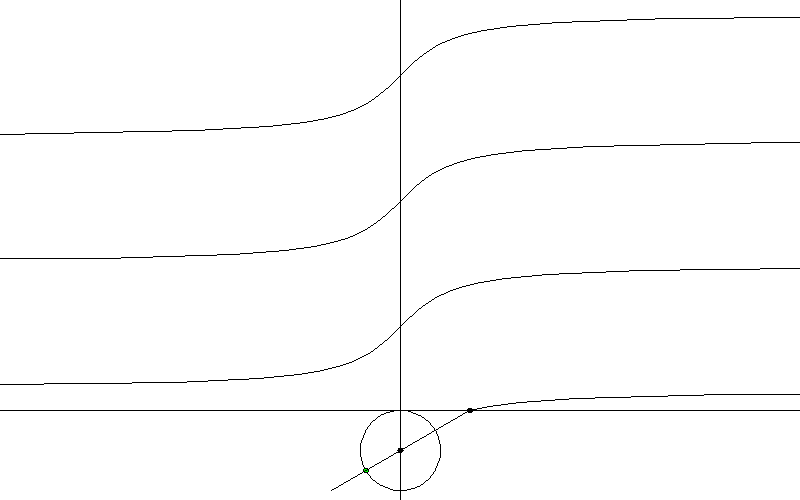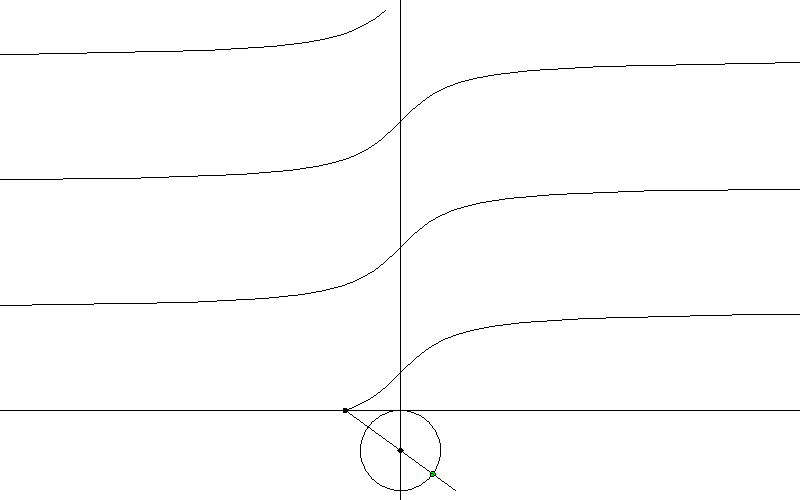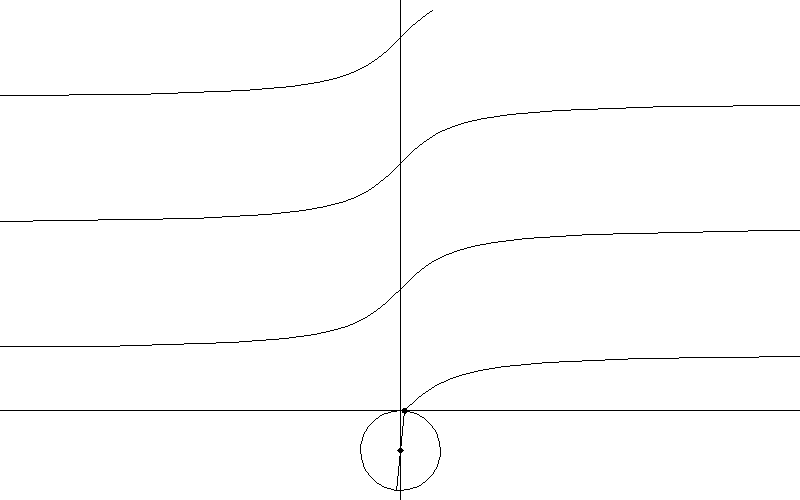
图7
八、圆规和正方形的爱恨纠缠
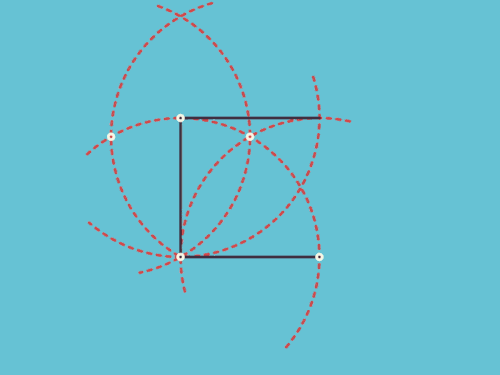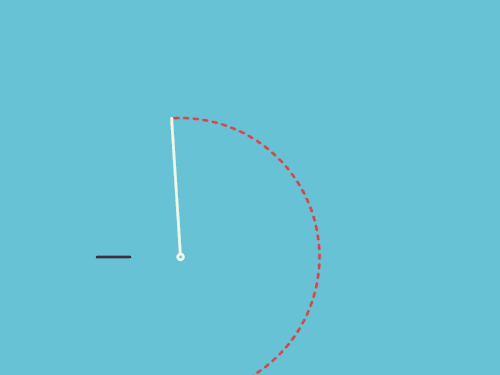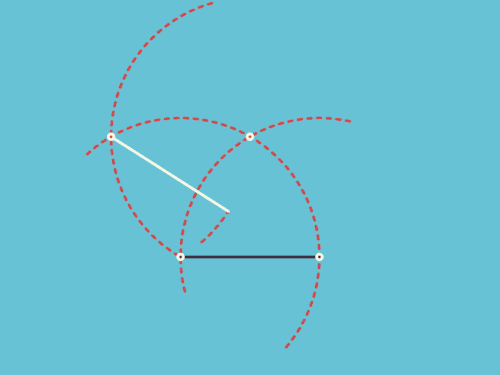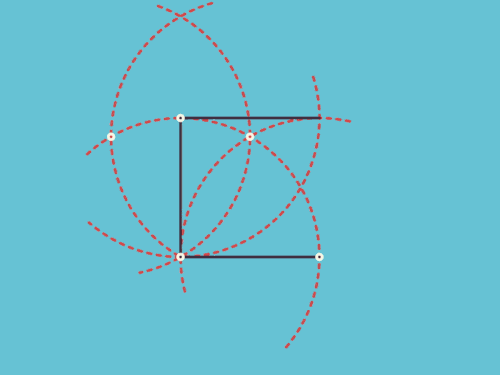
图8
九、多边形的外角之和总是等于360度
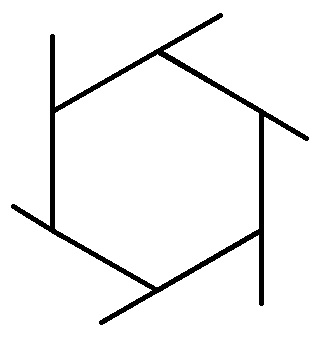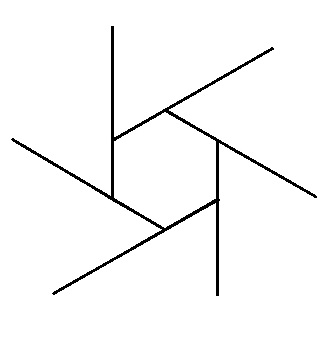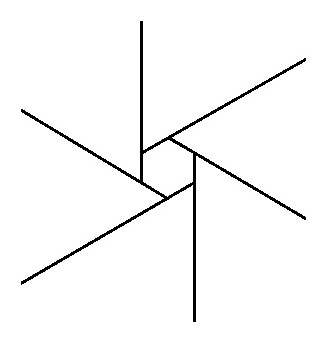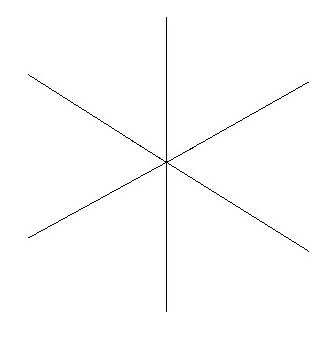
图9
十、认识椭圆的第一天,每个老师都会做的事
两个绿点,代表了坐在第一排,强制被叫上讲台按线头的两位同学。

图10
十一、余弦是正弦的衍生物
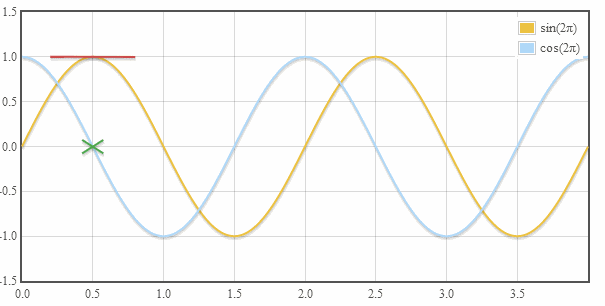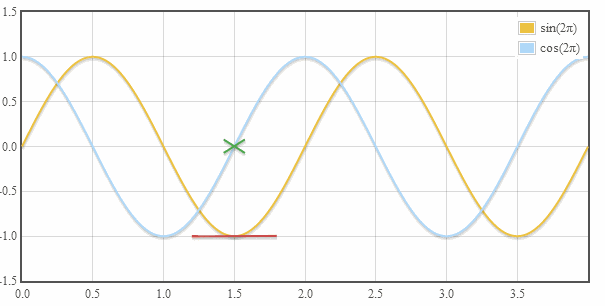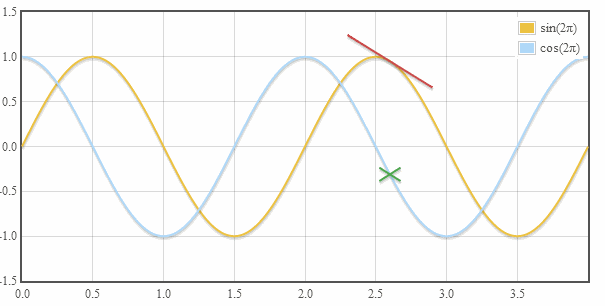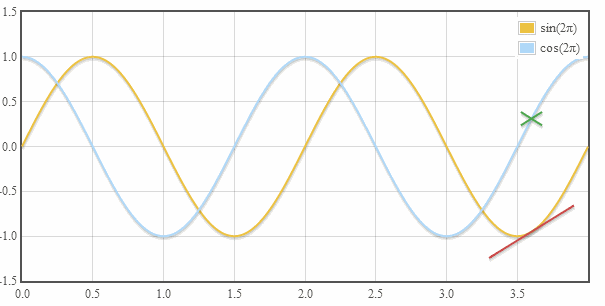
图11
十二、cos和sin的你追我赶
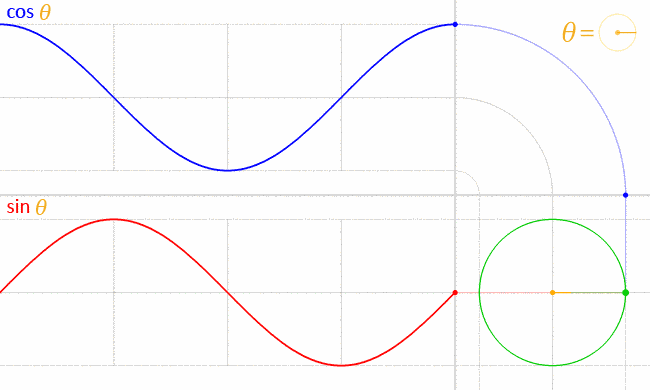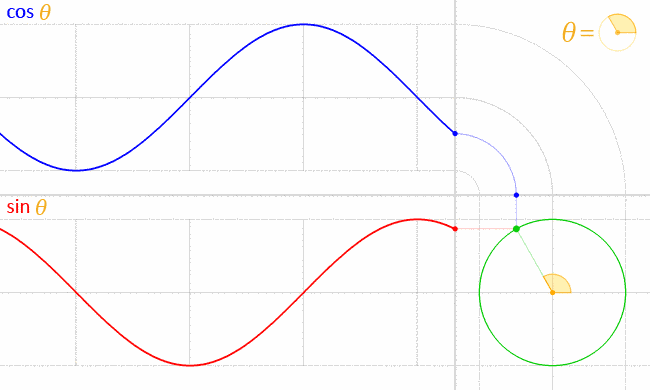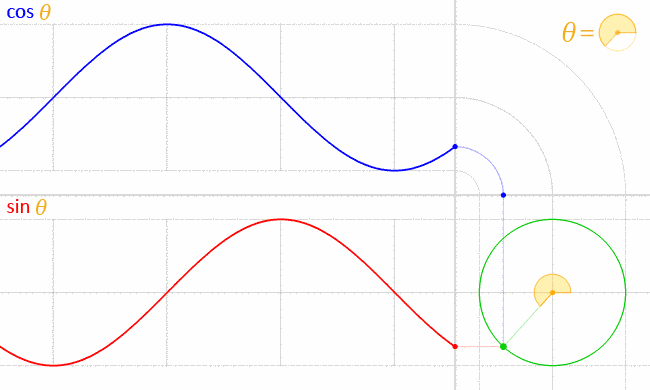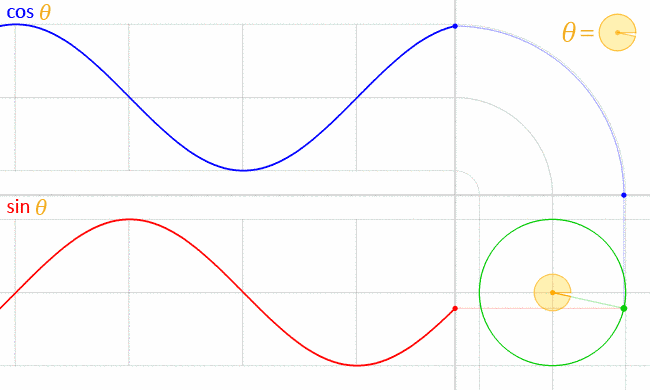
图12
十三、这是将sin和cos运用到三角形上
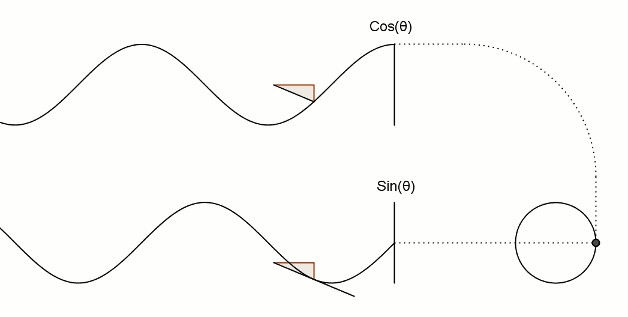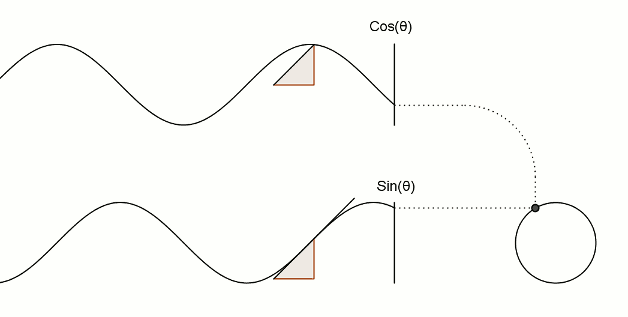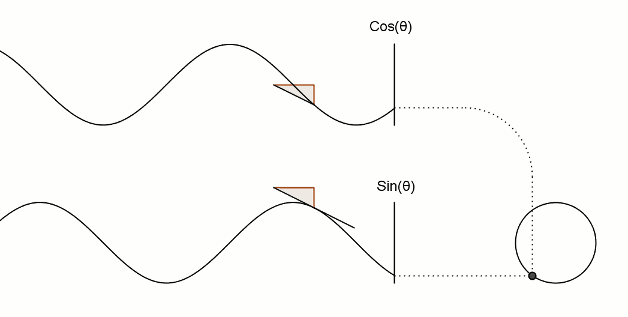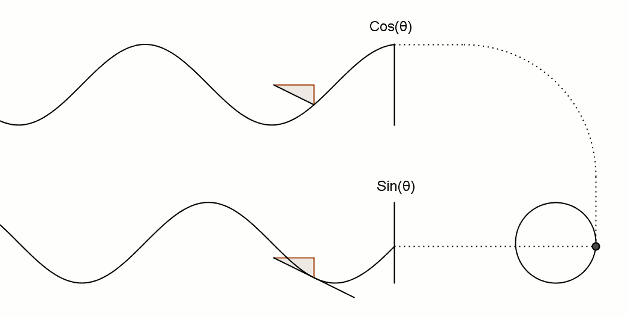
图13
十四、将一个公式从笛卡尔坐标转换成轴坐标
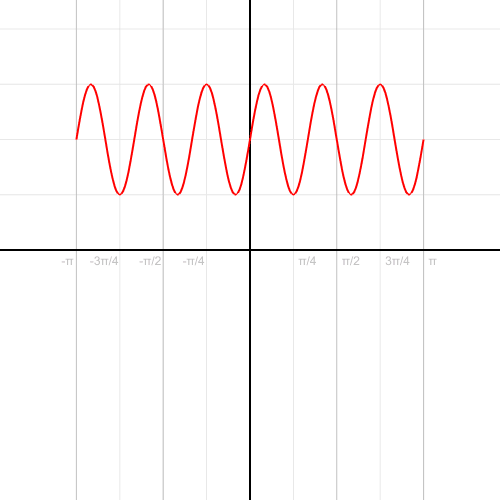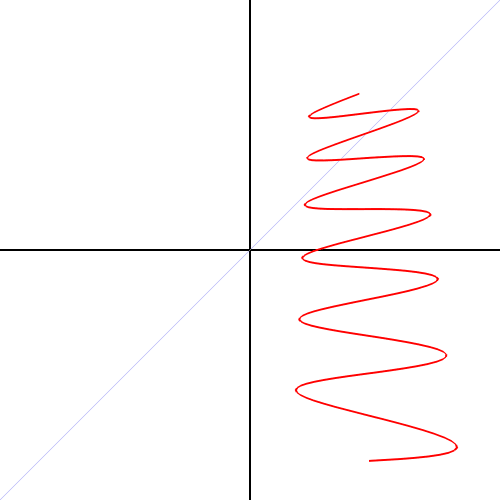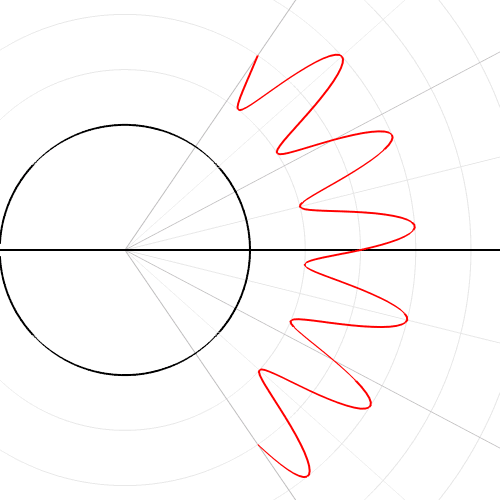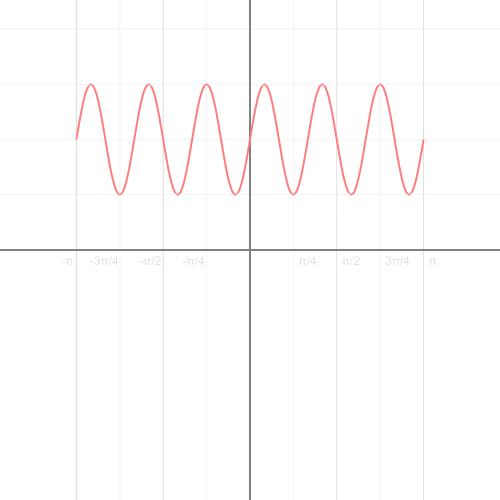
图14
十五、画抛物线
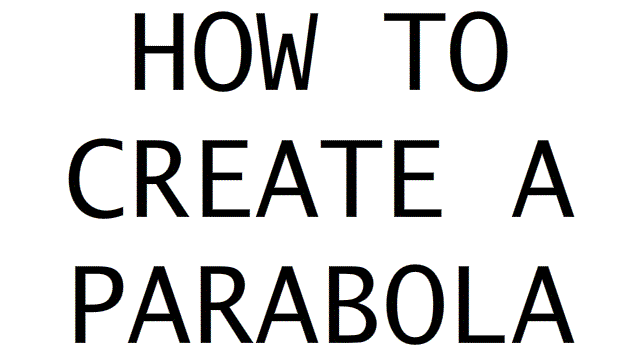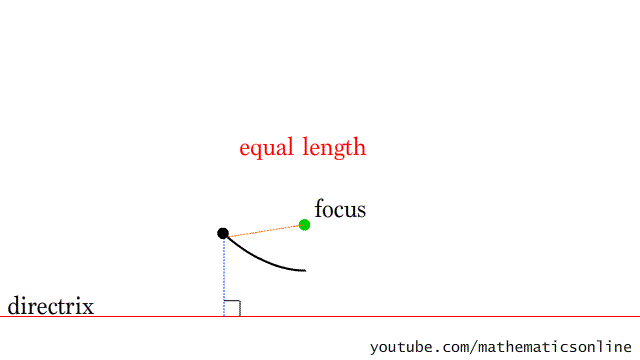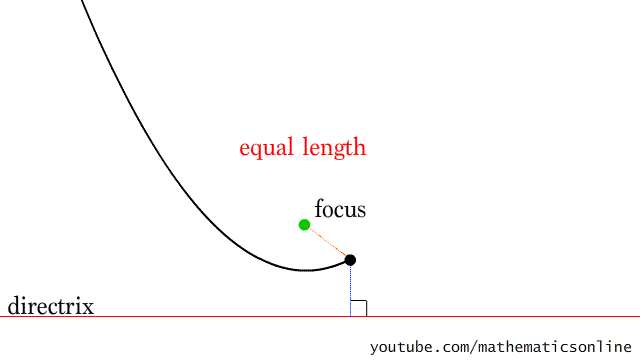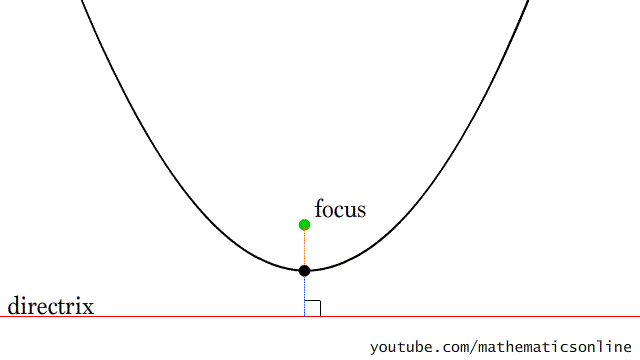
图15
十六、将双曲线表现成3D形式,也许你不相信,它完全是用直线画成的
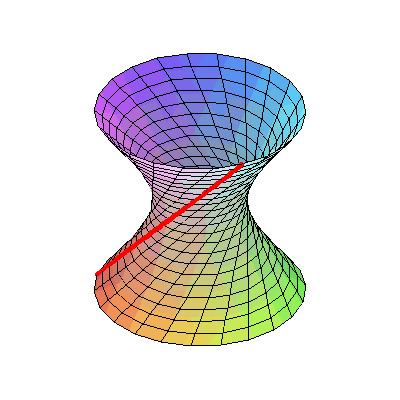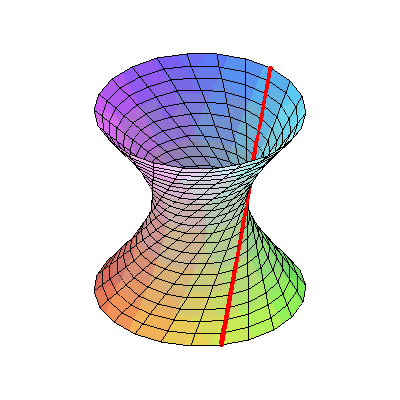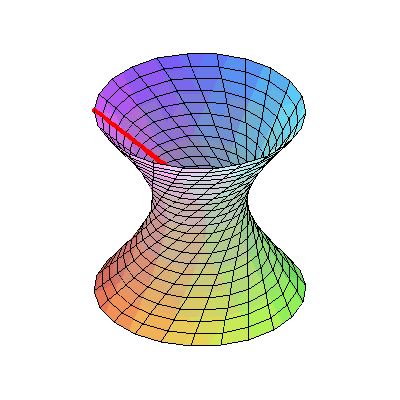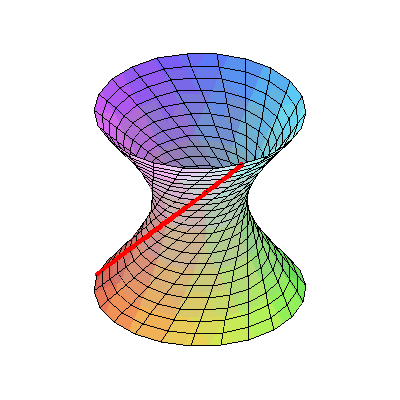
图16
十七、黎曼和(Riemann sum)约等于其曲线下的面积
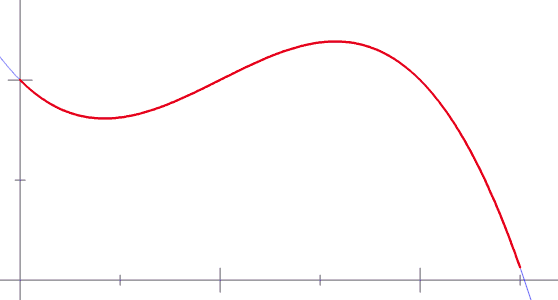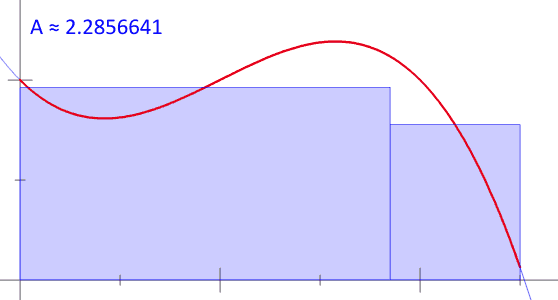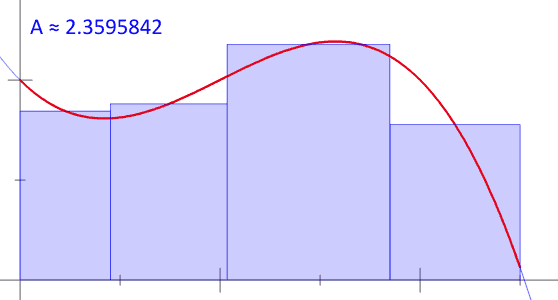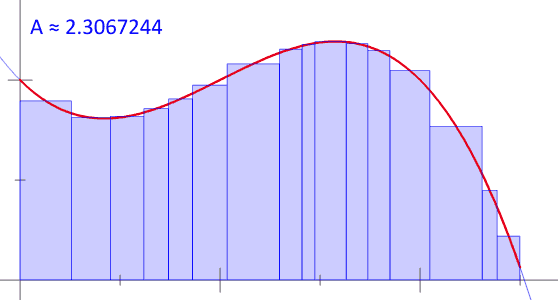
图17
十八、对数解法技巧
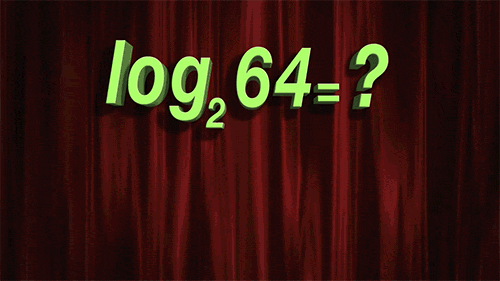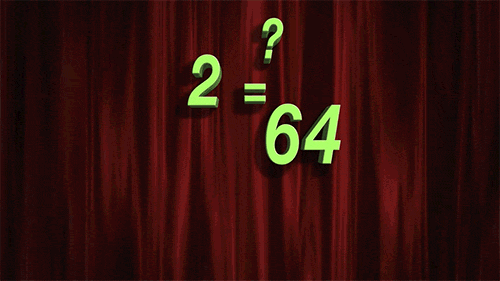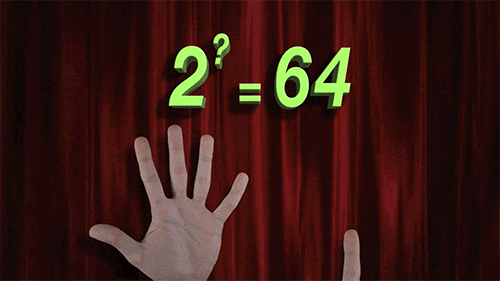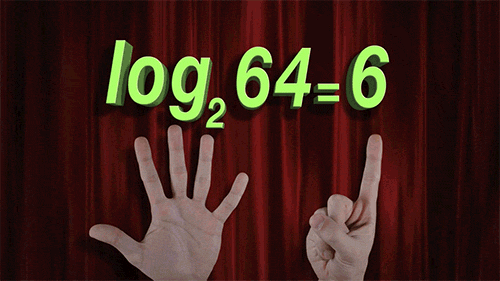
图18
十九、使用“FOIL”轻松的解决二项式乘法
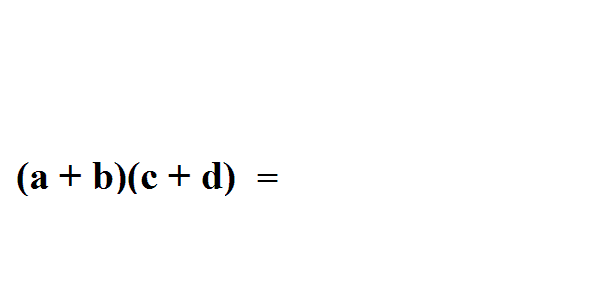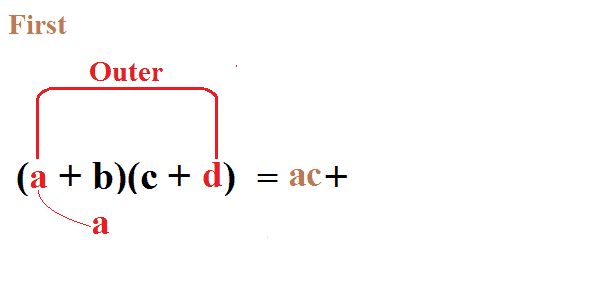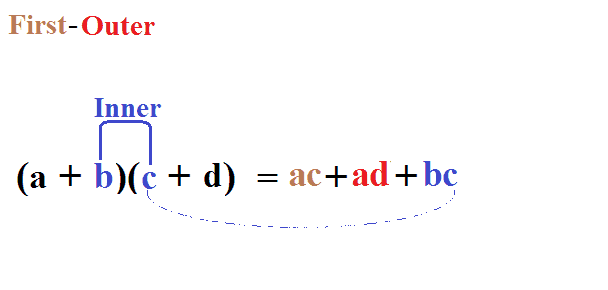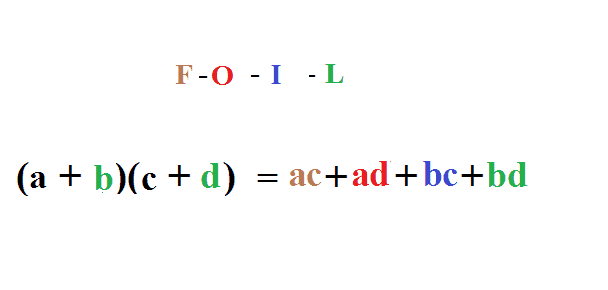
图19
二十、矩阵转置的技巧
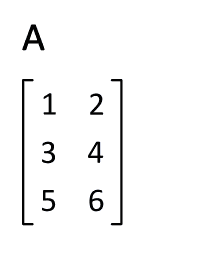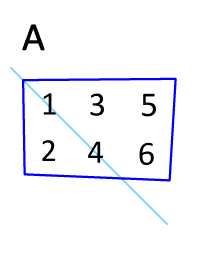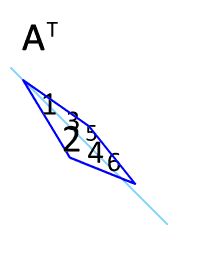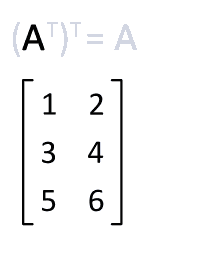
图20
二十一、杨辉三角问题(Pascal triangles)解法
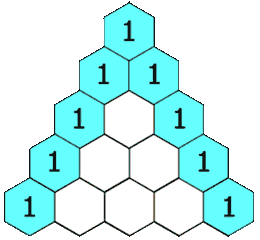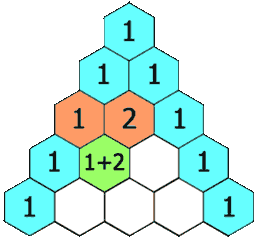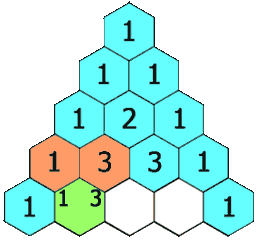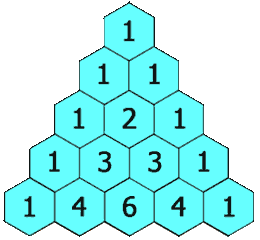
图21
二十二、谢尔宾斯基三角形
这是一种分形,在等边三角形里挖掉等边三角形再挖掉等边三角形再挖掉等边三角形……最后它得以永生。

图22
二十三、得到永生的证明

图23
二十四、最后,放一张数学家很会玩之胖子超人的诞生
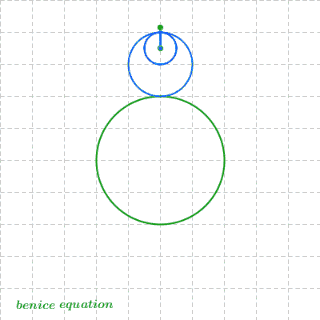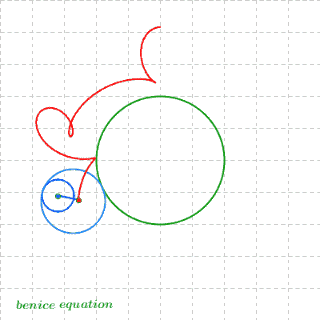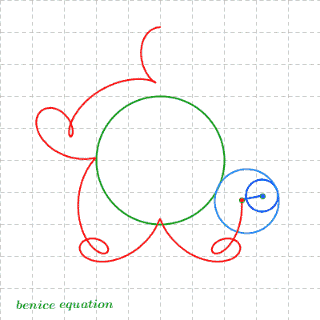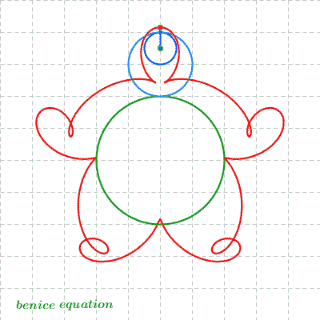
图24
心头浮现出浅浅欣慰又淡淡失落的感觉……这就是数学啊!
声明:文章根据网络公开资料整理,如有侵权请联系删除,谢谢。











