摘要:本文介绍了双摆曲线方程和双摆图像的Matlab实现,体验双摆曲线之美。
一、什么是双摆线

图1

图2:双摆的录屏

图3

图4:双摆的行为模拟

图5: 延时摄影拍摄的双摆轨迹

图6

图7

图8
双摆是物理中的一个概念,先给下单摆与双摆的定义:
单摆:由一根不可伸长、质量不计的绳子,上端固定,下端系一个质点的装置。
双摆:是一个摆的支点装在另一摆的下部所形成的组合物体。双摆有两个摆角,所以有两个自由度。双摆是多自由度振动系统的最简单的力学模型之一,它也是一种混沌实例。
将一根单摆连接在另一根的尾部,即为双摆。

图9
单摆是大家熟悉的,如果摆动幅度很小的话,是简单、确定、可预测的简谐运动。
如图10a所示的单摆,当角度很小时,摆动频率是单一的,可以看成是仅由摆长决定的简谐运动,相图是一个规则的椭圆(图10b)。但是在有外力的一定条件下,摆动幅度逐渐增大,新的频率分量将不断出现,有时还会产生转动模式,其振动及转动的次数、位置、方向,看起来越来越貌似随机和不确定,最后会过渡到图10c所示的混沌状态。

图10:单摆的混沌
将一根单摆连接在另一个单摆的尾部所构成的系统叫做双摆。双摆构造简单却很容易观察到复杂的混沌行为,见图11、图12。

图11

图12
二、双摆系统的微分方程组
利用拉格朗日力学获得双摆系统的微分方程组。拉格朗日力学是分析力学中的一种。於1788年由拉格朗日所创立,拉格朗日力学是对经典力学的一种的新的理论表述。
经典力学最初的表述形式由牛顿建立,它着重于分析位移,速度,加速度,力等矢量间的关系,又称为矢量力学。拉格朗日引入了广义坐标的概念,又运用达朗贝尔原理,求得与牛顿第二定律等价的拉格朗日方程。不仅如此,拉格朗日方程具有更普遍的意义,适用范围更广泛。还有,选取恰当的广义坐标,可以大大地简化拉格朗日方程的求解过程。
假设L1连接的球体的坐标为x1和y1,杆L2连接的球体的坐标为x2和y2,那么x1,y1,x2,y和两个角度之间有如下关系:
\(y_{1}=-L_{1}\cos \left ( \theta _{1} \right )\)
根据拉格朗日量的公式:
\( L=T-V\)
其中T为系统的动能,V为系统的势能,可以得到如下公式:
\(L=\frac{m_{1}}{2}\left ( \dot{x}_{1}^{2} +\dot{y}_{1}^{2}\right )+\frac{m_{2}}{2}\left ( \dot{x}_{2}^{2} +\dot{y}_{2}^{2}\right )-m_{1}gy_{1}-m_{2}gy_{2}\)
其中正号的项目为两个小球的动能,符号的项目为两个小球的势能。
将前面的坐标和角度之间的关系公式带入之后整理可得:
\(L=\frac{m_{1}+m_{2}}{2} L_{1}^{2}\dot{ \theta}_{1}^{2}+\frac{m_{2}}{2}L_{2}^{2} \dot{\theta}_{2}^{2}+m_{2}L_{1}L_{1}\dot{\theta}_{1}\dot{\theta}_{2}\cos \left ( \theta_{1}-\theta_{2} \right )+\left ( m_{1}+m_{2} \right )gL_{1}\cos\theta _{1}+m_{2}gL_{2}\cos\theta _{2}\)
对于变量θ1的拉格朗日方程:
\(\frac{\mathrm{d} }{\mathrm{d} x}\frac{\partial L}{\partial \dot{\theta} _{1}}-\frac{\partial L}{\partial \theta _{1}}=0\)
得到:
\(L_{1}\left [ \left ( m_{1}+m_{2} \right )L_{1} \ddot{\theta}_{1}+m_{2}L_{2}\cos \left ( \theta _{1}-\theta _{2}\right ) \ddot{\theta }_{2}+m_{2}L_{2}\sin \left ( \theta _{1}-\theta _{2}\right ) \dot{\theta }_{2}^{2}+\left ( m_{1}+m_{2} \right )g\sin \theta _{1} \right ]=0\)
对于变量θ2的拉格朗日方程:
\(\frac{\mathrm{d} }{\mathrm{d} x}\frac{\partial L}{\partial \dot{\theta} _{2}}-\frac{\partial L}{\partial \theta _{2}}=0\)
得到:
\(m_{2}L_{2}\left [L_{2} \ddot{\theta}_{2}+L_{1}\cos \left ( \theta _{1}-\theta _{2}\right ) \ddot{\theta }_{1}-L_{1}\sin \left ( \theta _{1}-\theta _{2}\right ) \dot{\theta }_{1}^{2}+g\sin \theta _{2} \right ]=0\)

图13

图14

图15

图16
三、双摆的Matlab程序实现
A=-2*g*sin(th1(1))-sin(th1(1)-th2(1))*thd2(1)^2;
J=-2*g*sin(al1(1))-sin(al1(1)-al2(1))*ald2(1)^2;
B=-g*sin(th2(1))+sin(th1(1)-th2(1))*thd1(1)^2;
K=-g*sin(al2(1))+sin(al1(1)-al2(1))*ald1(1)^2;
thdd1(1)=(A-B*cos(th1(1)-th2(1)))/(2-(cos(th1(1)-th2(1)))^2);
aldd1(1)=(A-B*cos(al1(1)-al2(1)))/(2-(cos(al1(1)-al2(1)))^2);
thdd2(1)=B-cos(th1(1)-th2(1))*thdd1(1);
aldd2(1)=B-cos(al1(1)-al2(1))*aldd1(1);
X1(1)=sin(th1(1));
Y1(1)=cos(th1(1));
D1(1)=sin(al1(1));
Z1(1)=cos(al1(1));
X2(1)=sin(th1(1))+sin(th2(1));
Y2(1)=cos(th1(1))+cos(th2(1));
D2(1)=sin(al1(1))+sin(al2(1));
Z2(1)=cos(al1(1))+cos(al2(1));
for i=2:N
thd1(i)=thd1(i-1)+dt*thdd1(i-1);
ald1(i)=ald1(i-1)+dt*aldd1(i-1);
thd2(i)=thd2(i-1)+dt*thdd2(i-1);
ald2(i)=ald2(i-1)+dt*aldd2(i-1);
th1(i)=th1(i-1)+dt*thd1(i);
al1(i)=al1(i-1)+dt*ald1(i);
th2(i)=th2(i-1)+dt*thd2(i);
al2(i)=al2(i-1)+dt*ald2(i);
A=-2*g*sin(th1(i))-sin(th1(i)-th2(i))*thd2(i)^2;
J=-2*g*sin(al1(i))-sin(al1(i)-al2(i))*ald2(i)^2;
B=-g*sin(th2(i))+sin(th1(i)-th2(i))*thd1(i)^2;
K=-g*sin(al2(i))+sin(al1(i)-al2(i))*ald1(i)^2;
thdd1(i)=(A-B*cos(th1(i)-th2(i)))/(2-(cos(th1(i)-th2(i)))^2);
aldd1(i)=(J-K*cos(al1(i)-al2(i)))/(2-(cos(al1(i)-al2(i)))^2);
thdd2(i)=B-cos(th1(i)-th2(i))*thdd1(i);
aldd2(i)=K-cos(al1(i)-al2(i))*aldd1(i);
X1(i)=sin(th1(i));
D1(i)=sin(al1(i));
Y1(i)=cos(th1(i));
Z1(i)=cos(al1(i));
X2(i)=sin(th1(i))+sin(th2(i));
D2(i)=sin(al1(i))+sin(al2(i));
Y2(i)=cos(th1(i))+cos(th2(i));
Z2(i)=cos(al1(i))+cos(al2(i));
plot([0, X1(i), X2(i)], [0, -Y1(i), -Y2(i)],'-o');
hold on
plot([0, D1(i), D2(i)], [0, -Z1(i), -Z2(i)],'-o');
axis([-2 2 -2 2]);
title(['t = ', num2str(double(i)*dt, '% 5.3f'), ' s']);
hold on
plot(X2(1:i), -Y2(1:i), 'r');
plot(D2(1:i), -Z2(1:i), 'g');
hold off
drawnow;
end
四、双摆绘制的图像

图17
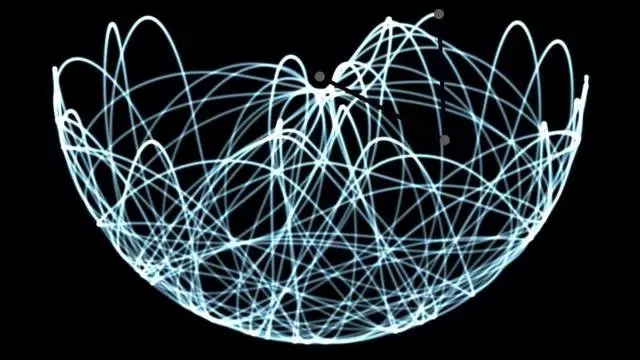
图18

图19
声明:文章转自微信公众号【YaK芽课】,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











