摘要:数学一向以严谨的思维著称,每一步推理都需要严格的理由。但在数学历史中,漏洞百出的数学推理也频频出现。有趣的是,即使是这些不严格的思路也充满着智慧,在数学中的地位不亚于那些伟大的证明。今天,果壳死理性派会用几个经典例子告诉你,在数学里也是可以耍流氓的。
一、逻辑中的那些流氓
耍流氓是各种数学悖论的来源。你能想一个命题,使得它和它的否定形式同时成立吗?令人难以置信的是,这样的命题真的存在。“这句话是七字句”就是这样一种奇怪的命题。它的否定形式是“这句话不是七字句”,同样是成立的。
你肯定会大叫“赖皮”,命题的真假与这个命题本身的形式有关,这样的命题算数学命题吗?没错,这些涉及到自己的命题都叫做“自我指涉命题”,它们的出现会引发很多令人头疼的问题。从说谎者悖论(Liar paradox)到罗素悖论(Russell's paradox),各种逻辑悖论的产生根源几乎都是自我指涉。数理逻辑中的流氓遍地都是,它们直接引发了数学史上的第三次数学危机。

图1
二、欧拉的流氓证明法
在数学史上,很多漂亮的定理最初的证明都是错误的。最典型的例子可能就是1735年大数学家欧拉(Euler)的“证明”了。他曾经仔细研究过所有完全平方数的倒数和的极限值,并且给出了一个漂亮的解答:
\(\frac{1}{1^{2}}+\frac{1}{2^{2}}+\frac{1}{3^{2}}+\frac{1}{4^{2}}+\cdot \cdot \cdot =\frac{\pi ^{2}}{6}\)
这是一个出人意料的答案,圆周率π毫无征兆地出现在了与几何完全没有关系的场合中。欧拉的证明另辟蹊径,采用了一种常人完全想不到的绝妙方法。他根据方程sin(x)/x=0的解,对sin(x)/x的级数展开进行因式分解,再利用对比系数的方法神奇地得到了问题的答案。不过,利用方程的解进行因式分解的方法只适用于有限多项式,在当时的数学背景下,这种方法不能直接套用到无穷级数上。虽然如此,欧拉利用这种不严格的类比,却得出了正确的结果,欧拉大师耍了一个漂亮的流氓。
三、最经典的“无字证明”
一些定理的直观理解虽然毫无逻辑可言,完全算不上是数学证明,但这些精巧而欢乐的视角,依然让数学家们如痴如醉。
1989年的《美国数学月刊》(American Mathematical Monthly)上有一个貌似非常困难的数学问题:下图是由一个个小三角形组成的正六边形棋盘,现在请你用右边的三种(仅朝向不同的)菱形把整个棋盘全部摆满(图中只摆了其中一部分),证明当你摆满整个棋盘后,你所使用的每种菱形数量一定相同。
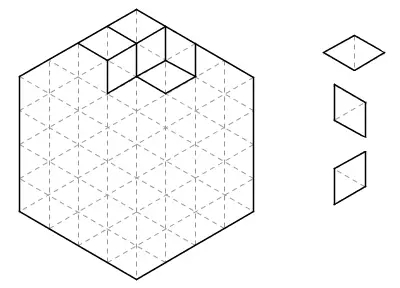
图2
文章末尾提供了一个非常帅的“证明”。把每种菱形涂上一种颜色,整个图形瞬间有了立体感,看上去就成了一个个立方体在墙角堆叠起来的样子。三种菱形分别是从左侧、右侧、上方观察整个立体图形能够看到的面,它们的数目显然应该相等。
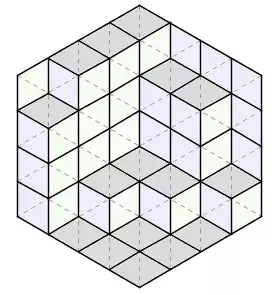
图3
严格地说,这个本来不算数学证明的。但它把一个纯组合数学问题和立体空间图形结合在了一起,实在让人拍案叫绝。因此,这个问题及其鬼斧神工般的“证明”流传甚广,深受数学家们的喜爱。《最迷人的数学趣题——一位数学名家精彩的趣题珍集》(Mathematical Puzzles: A Connoisseur's Collection)一书的封皮上就赫然印着这个经典图形。在数学中,类似的流氓证明数不胜数,不过上面这个可能算是最经典的了。

图4:《最迷人的数学趣题——一位数学名家精彩的趣题珍集》的封面
四、旋轮线的面积

图5:旋轮线,图片来源:Wikipedia
车轮在地上旋转一圈的过程中,车轮圆周上的某一点划过的曲线就叫做“旋轮线”。在数学和物理中,旋轮线都有着非常重要而优美的性质。比如说,一段旋轮线下方的面积恰好是这个圆的面积的三倍。这个结论最早是由伽利略(Galileo Galilei, 1564-1642)发现的。不过,在没有微积分的时代,计算曲线下方的面积几乎是一件不可能完成的任务。伽利略是如何求出旋轮线下方的面积的呢?
他的方法简单得实在是出人意料:它在金属板上切出旋轮线的形状,拿到秤上称了称,发现重量正好是对应的圆形金属片的三倍。
在试遍了各种数学方法却都以失败告终之后,伽利略果断地耍起了流氓,用物理实验的方法测出了图形的面积。用物理实验解决数学问题也不是一件稀罕事了,广义费马点(generalized Fermat point)问题就能用一套并不复杂的力学系统解出,施泰纳问题(Steiner tree problem)也可以用肥皂膜实验瞬间秒杀。
声明:文章转自Matrix67博客,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











