摘要:在中国,“八”谐音“发”,成了一个人见人爱的幸运数字。不管是手机号,还是车牌号,谁都想要里面有个数字8,含有数字8的数似乎成了一种不可再生的稀缺资源。死理性派自然而然地想到一个问题:在全体自然数中,含有数字8的数占多大的比例?10%?50%?还是90%?
一、前n位数里有多少个含有8的数字?
如果把0算上的话,一位数一共有10个,不过含有数字8的只有一个,只占总数的10%。那么,在两位以内的所有数中,含有数字8的数是不是也只占10%呢?不是的。从0数到99,一共有100个数,但含有8的数字有8,18,28,…,78,80,81,82,…,88,89,98,一共有19个。也就是说,两位以内的所有数中,含有数字8的数占了19%。
如果进一步扩大我们考虑的自然数范围,你会发现这个比值会越来越大。计算机显示,在0到9999999999之间的数中,含有数字8的数竟然占到了65.1%。
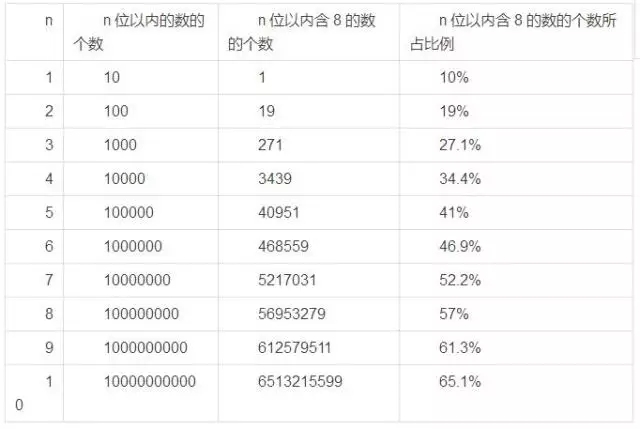
图1(利用计算机程序运算得到的表格:对于不同的n,n位以内含8的数的个数所占的比例)
二、当n趋于无穷大的时候
为了得到全体自然数中含8的数所占的百分比,我们需要算出,如果上表中的n增加到无穷大,表格最右列的那个百分比会变成多少。为此,我们首先需要推导出表格最右列的百分比有什么计算公式。
在考虑n位以内的所有数时,我们可以在不足n位的数的前面添0补足。这样一来,每个数都可以看作是恰好由n个0到9之间的数字组成的。显然,所有这样的数一共有10n个,但其中不含数字8的数(也就是只含有数字0,1,2,…,7,9的数)却只有9n个。因此,不含数字8的数占了所有数的9n/10n=0.9n,含有数字8的数所占比例也就是1-0.9n了。
当n趋于无穷大,0.9n将会越来越小,最终变成0,此时1-0.9n也就变成了1。因此,结论就是:含有数字8的数占了全体自然数的100%!也就是说,几乎所有数都是含有数字8的。
这不是玩笑,含有数字8的数真的占了全体自然数的100%。当样本空间无穷大时,100%并不等于一定会发生,同理0%也并不等于一定不发生。比方说,射箭正中靶心的概率就是0,因为射中靶中某个特定区域的概率就是这块区域的面积比上整个圆的面积,而由于圆心这一个点的“面积”为0,因此它比上整个圆的面积仍为0,也即正中靶心的概率为0。
三、缺8数
含有数字8的数竟有这么神奇的发现,不过小编表示不含数字8的“缺8数”,更具有神秘色彩。顾名思义,缺8数就是指在自然数12345679中没有8,所以被称为“缺8数”。虽然看起来平淡无奇,但细细研究,却能发现其有非常多奇妙的性质。
1. “清一色”
缺8数在乘1至81中的9的倍数可以得到“清一色”,例如:
12345679 × 9=111111111
12345679 × 18=222222222
12345679 × 27=333333333
12345679 × 36=444444444
12345679 × 45=555555555
12345679 × 54=666666666
12345679 × 63=777777777
12345679 × 72=888888888
12345679 × 81=999999999
2. “三位一体”
缺8数乘以3的倍数但不是9的倍数的数(12起),可以得到“三位一体”,例如:
12345679 × 12=148148148
12345679 × 15=185185185
12345679 × 21=259259259
12345679 × 24=296296296
12345679 × 30=370370370
12345679 × 33=407407407
12345679 × 42=518518518
12345679 × 48=592592592
12345679 × 51=629629629
12345679 × 57=703703703
12345679 × 78=962962962
3. “走马灯”
当缺8数乘以19时,其积将是234567901,像走马灯一样,原先居第二位的数2却成了开路先锋。例如:
12345679 × 19=234567901
12345679 × 28=345679012
12345679 × 37=456790123
12345679 × 46=567901234
深入的研究显示,当乘数为一个公差等于9的算术级数时,出现“走马灯”的现象。例如:
12345679 × 8=098765432
12345679 × 17=209876543
12345679 × 26=320987654
12345679 × 35=432098765
现在,我们又把乘数依次换为10,19,28,37,46,55,64,73(它们组成公差为9的等差数列):
12345679 × 10=123456790
12345679 × 19=234567901
12345679 × 28=345679012
12345679 × 37=456790123
12345679 × 46=567901234
12345679 × 55=679012345
12345679 × 64=790123456
12345679 × 73=901234567
以上乘积全是“缺8数”!数字1,2,3,4,5,6,7,9像走马灯似的,依次轮流出现在各个数位上。
4. “回文现象”
将缺8数乘以各位都是9的数,奇迹出现了!等号右边全是回文数,而且,这些回文数全是“阶梯式”上升和下降,神奇、优美、有趣!
12345679 × 9=111111111
12345679 × 99=1222222221
12345679 × 999=12333333321
12345679 × 9999=123444444321
12345679 × 99999=1234555554321
12345679 × 999999=12345666654321
12345679 × 9999999=123456777654321
12345679 × 99999999=1234567887654321
12345679 × 999999999=12345678987654321
声明:文章转自【WMO世奥赛组委会】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











