摘要:本文介绍分形的提出和特点,以及传统几何与分形几何的区别。
第一次了解分形艺术,是在一个贴子中无意发现的,当时我看到那些美丽的光,有一种莫名的亲切感。我自己从事摄影,有关于艺术和美学的事物,总会多看几眼。刚好那段时间有做喜悦曼陀罗的练习,只要和光有关的,我总会格外的敏感。

图1
接着,我开始认识到了数学意义上的分形,比如下面这张图片是一段代码表现出来的:

图2

图3
一、分形的提出
1975年Mandelbrot在其《自然界中的分形几何》一书中引入了分形(fractal)这一概念。从字面意义上讲,fractal是碎块、碎片的意思。然而这并不能概括Mandelbrot的分形概念,但在数学上大家都认为分形有以下几个特点:
1. 无限精细的结构,比例自相似性
这张图片完美的表现了分形的两个重要的特性:无限精细的结构,比例自相似性,自相似性是分形的灵魂,它使得分形的任何一个片段都包含了整个分形的信息。因为图片是代码生成,所以不存在像素问题,放大任何一个点都可以,如果你脑洞够大,你可以理解为:时间线。
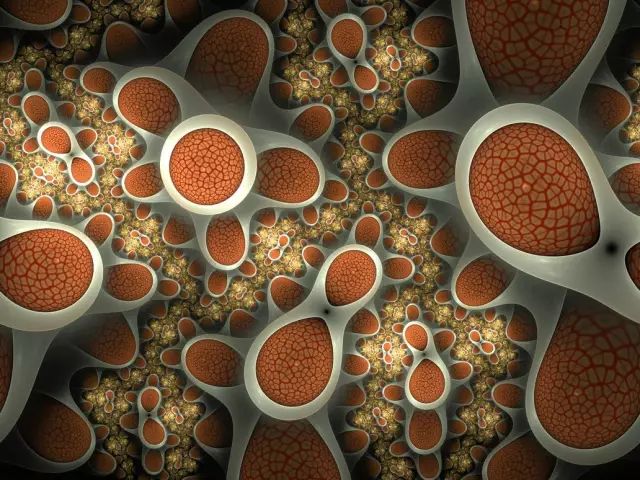
图4
2. 分数维大于它的拓扑维数
关于这点,有人举了一个例子进行说明,说实话,我自己也没怎么看懂 ,虽然我也当过数学课代表,百度上搜索的答案是这样的:

图5
老子说:故常无欲以观其妙,常有欲以观其徼。此两者同出而异名,同谓之玄。玄之又玄,众妙之门。
上面话的意思就是妙与徼的关系就是玄。而上面的分形公式就刚好表达了老子的意思,无穷小与无穷大就存在一个公式当中,这个公式的名字叫做:玄,配合下面的分形图片就更好理解了。
图中每一个小图案就是我们每一个灵魂,我们每一个灵魂代表了无穷小的个体。但我们无穷小的每个个体,都有宇宙爸爸无穷大的智慧。
原来数学真美,是吧?

图6
二、传统几何和分形的区别
传统几何其研究的是在旋转、平移、对称变换下各种不变的量,如角度、长度、面积、体积,其适用范围主要是人造的物体。
而分形的历史只有20来年,它由递归、迭代生成,主要适用于自然界中形态复杂的物体。分形几何不再以分离的眼光看待分形中的点、线、面,而是把它看成一个整体。
能代表分形几何这个亲近自然特性的最好例子就是斐波纳契数:

图7(点击观看斐波那契数的介绍视频)
从根本上讲分形反映了自然界中某些规律性的东西,以植物为例,植物的生长是植物细胞按一定的遗传规律不断发育、分裂的过程。这种按规律分裂的过程可以近似地看作是递归、迭代过程,这与分形的产生极为相似。在此意义上,人们可以认为一种植物对应一个迭代函数系统。人们甚至可以通过改变该系统中的某些参数来模拟植物的变异过程。
分形几何也就是自然几何,以分形或分形的组合的眼光来看待周围的物质世界就是自然几何观。
分形几何,让数学来推演生命的演化从此有了可能。又或许,分形几何是造物主留给人类的一把钥匙,从男性能量(逻辑思维)的角度接近造物主,也成为了可能。

图8

图9

图10

图11

图12

图13
声明:文章转自【知乐日记】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











