摘要:从海螺和螺旋星云到人类的肺脏结构,我们身边充满各种各样的混沌图案。分形(一种几何形状,被以越来越小的比例反复折叠而产生不能被标准几何所定义的不标准的形状和表面)是由混沌方程组成,它包含通过放大会变的越来越复杂的自相似图案。要是把一个分形图案分成几小部分,结果会得到一个尺寸缩小,但形状跟整个图案一模一样的复制品。
分形的数学之美,是利用相对简单的等式形成无限复杂的图案。它通过多次重复分形生成等式,形成美丽的图案。我们已经在我们的地球上搜集到一些这方的天然实例,下面就让我看一看。
一、罗马花椰菜:拥有黄金螺旋
这种花椰菜的变种是最重要的分形蔬菜。它的图案是斐波纳契数列,或称黄金螺旋型(一种对数螺旋,小花以花球中心为对称轴,螺旋排列)的天然代表。

图1:罗马花椰菜
二、世界最大盐沼——天空之镜

图2:盐沼
过去一个世纪,上图里的旧金山海湾盐沼一直被用来进行工业盐生产。
下图显示的是位于玻利维亚南部的世界最大盐沼——天空之镜(Salar de Uyuni)。坚硬的盐层上呈现非常一致的不规则图案,这是典型的分形。

图3:天空之镜
三、菊石缝线
在大约6500万年前灭绝的菊石,是制作分成许多间隔的螺旋形外壳的海洋头足纲动物。这些间隔之间的壳壁被称作缝线,它是分形复曲线。美国著名古生物学家史蒂芬·杰伊·古尔德依据不同时期的菊石缝线的复杂性得出结论说,进化并没驱使它们变得更加复杂,我们人类显然是“一个例外”,是宇宙里独一无二的。菊石的外壳还生长成一个对数螺旋型,很显然,自然界经常会出现这种图案,例如罗马花椰菜。

图4:大约6500万年前灭绝的菊石

图5:菊石缝线
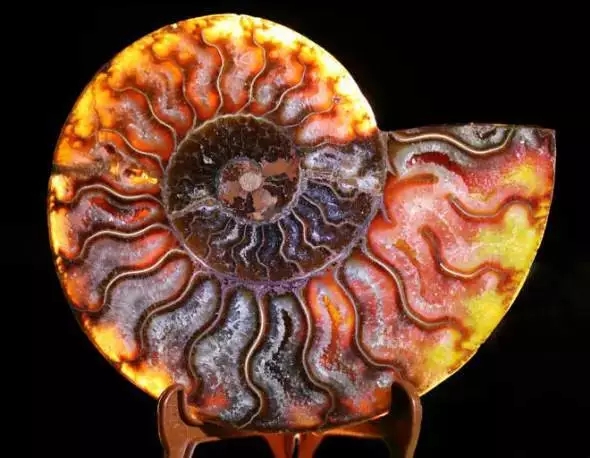
图6:菊石的外壳还生长成一个对数螺旋型
四、山脉
山脉是构造作用力和侵蚀作用的共同产物,构造作用力促使地壳隆起,侵蚀作用导致一些地壳下陷。这些因素共同作用的产物,是一个分形。下图显示的是喜马拉雅山脉,它是世界很多最高峰的所在地。印度板块和欧亚板块在大约7000万年前相撞在一起,导致喜马拉雅山脉隆起,现在这座山脉的高度仍在不断增加。

图7:喜雅拉马山脉
五、蕨类植物
蕨类植物是一种常见的自相似图案,这意味着它们的图案能以任何放大率或缩小率生成和复制。描述蕨类植物的数学公式是根据迈克尔·巴恩斯利的名字命名的,它是第一个显示这种混沌状态是不可预知的,而且一般是遵循确定性法则(以非线性循环方程组为基础)。也就是说,利用巴恩斯利的蕨类植物公式反复生成的任意数字,最终生成一个独一无二的蕨类植物形状的物体。

图8:蕨类植物
六、云团

图9:云团
上图中的海上层状云团是“阿卡”卫星在非洲西海岸附近的南太平洋上空拍到的。分形云团图案,被一系列斜纹状云团分开。据美国宇航局“地球观测台”说,在这种连续云团中看到这么明显的分界线,实属罕见,至今科学家还无法解释清楚它是如何形成的。
据美国宇航局说,下图里长达200英里(321.87公里)的一系列云旋,它可能是迄今为止拍到的这种形式的最长云团。这些云旋又被称作冯·卡门云街(von Kármán cloud streets),是根据已故流体动力学家西奥多·冯·卡门的名字命名的。当低空云团被岛屿等物体中断时,就会形成云街。机翼下方的风有时也会形成这种图案。

图10:长达200英里(321.87公里)的一系列云旋
七、叶子
很多植物的分枝和叶片形状都遵循着简单的递推公式。

图11:叶子
具有讽刺意味的是,沿主干道、二级和三级路线进行的森林砍伐模式,也形成了类似图案,例如下图中显示的巴西西部朗多尼亚州的森林砍伐图,这是亚马逊流域森林砍伐最严重的一个地区。

图12:巴西西部朗多尼亚州的森林砍伐图
八、峡谷

图13:美国大峡谷的伪彩色图
上面这张美国大峡谷的伪彩色图,展示的是由科罗拉多河在长达数百万年间创造的一个分形图案。图片上的红色代表植被区。
下图显示的是亚利桑那州柴利峡谷国家古迹的伪彩色图。美国国家公园管理局称,它是北美洲最长的连续性有人居住峡谷地形。

图14:亚利桑那州柴利峡谷国家古迹的伪彩色图
九、闪电

图15:闪电
闪电在向地面移动时,它的路径是逐步形成的,闪电把空气转变成等离子体。

图16
十、孔雀毛

图17:孔雀毛
孔雀利用羽毛上的重复图案吸引交配对象。

图18
十一、雪花
雪花里和霜表面的结晶水形成重复图案。

图19:雪花
十二、瀑布
瀑布跟峡谷类似,水流从陡峭的岩脊一侧流过时,不规则的岩石组合和重力导致重复图案产生。

图20:瀑布
十三、河流三角洲
育空河在汇入阿拉斯加州近海的白令海以前,分支成数千条支流。该河从图上的左侧流过,白令海位于图片的左侧较远处。

图21:河流三角洲
声明:文章转自【知识探索】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











