排队实在是一件烦人的事情,但又总是无可避免。排队时我们最想知道的是什么呢?肯定是还要等多久嘛。既然想知道,就把它算出来嘛,反正等着也是等着。
我们先建立一个清晰的排队模型:现在有一个服务窗口,任何时间只能为一名客户办理业务。每间隔2分钟到10分钟,就会新增一位客户。每位客户办理业务的时间在5分钟到8分钟之间。假定相邻客户到达窗口时间间隔和客户业务办理时间分别在各自的时间区间内线性分布,并且是整数。
在给出一般算法之前,可以模拟一个简单的情况:考虑一共来5名客户的情况。比如我们可以假设数据是这样的:
客户 客A 客B 客C 客D 客E
相邻客户到达时间间隔 3 4 8 2 7
业务办理时间 5 5 6 7 8
客户A在t=0 时刻的3分钟后到达,所以窗口在开始空闲了3分钟。客户A到了即可以办理业务(前面没人),用时3分钟,期间客B在 t=3+4=7 分钟时到来,此时客B还在办理业务,在客A业务办理完毕前,即 t=3+5=8 分钟前客B处于等待状态,等待时间为 8-7=1 分钟。我们把它直观的反应时间轴上,每个人的等待与业务办理时间都很容易看出来:
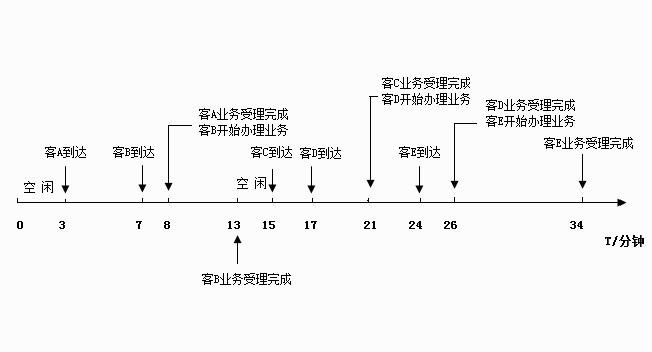
图1
下表显示了5名客户这个情况下的模拟结果。5名客户共计等待时间是7分钟,这个等待时间对客户来说是一种成本与心理上的负担,等待过久恰就是我们产生不满、大声抱怨的重要原因。窗口有5分钟时间处于空闲状态,约占整个模拟时间(34分钟)的14.7%。
模拟结果如下:
客户序号 到达时间 开始服务时间 等待时间 排队长度 服务完毕时间 逗留时间(T:分钟)
A 3 3 0 0 8 5
B 7 8 1 1 13 6
C 15 15 0 0 21 6
D 17 21 4 1 26 9
E 24 26 2 1 34 10
注:平均等待时间:1.4分钟 平均业务受理时间:6.2分钟 平均逗留时间:7.2分钟
用蒙特·卡洛方法模拟实际情况
现实中,办理业务人远远超过5个人,而人一多,等待时间就更长。我们以上述算法为基本模型,使用蒙特·卡洛方法,通过在计算机软件(比如MATLAB)产生伪随机数实现统计模拟,获取近似解。
下面以200名客户为限,独立模拟6次的结果(最后一栏为平均值):
在窗口平均逗留时间(min) 33 23 58 16 30 14 32
在窗口最长逗留时间(min) 60 50 89 43 54 40 67
平均等待时间(min) 26 16 51 9 24 8 25
最长等待时间(min) 54 43 84 37 47 35 60
窗口空闲时间百分比 0.68% 1.14% 0.23% 2.60% 0.60% 4.04% 1.86%
从表中很容易看到,你不过去办个很轻松的业务(比如电信缴费),居然需要等上半小时左右,运气再差点,一个小时都不算啥!于是我们焦急的盼望快点快点再快点,但是窗口的工作率已经近乎100%,很难再有所提升。假如商家多开了一个窗口(将多种业务分类,分工导致专业化)或者使用了更快的业务受理系统,从而使业务受理时间缩短2分钟,将会发生什么?
业务时间缩短2分钟的模拟结果(最后一栏为平均值):
在窗口平均逗留时间(min) 7 6 6 5 6 5 5.8
在窗口最长逗留时间(min) 25 14 18 17 16 12 20.4
平均等待时间(min) 2 2 2 1 1 1 1.5
最长等待时间(min) 22 10 12 11 10 9 12.3
窗口空闲时间百分比 26.61% 23.82% 25.00% 26.54% 28.40% 27.64% 26.34%
我们看到,最长也不过需要等待12分钟就可以完事,无疑效率大大提高了。但是另一方面,窗口空闲率上升了很多!所以窗口不是说多开就多开的。但是,等待时间缩短也许可以吸引更多的客户,导致相邻客户到达时间间隔缩短为2—8分钟,我们再来看看结果:
在窗口平均逗留时间(min) 8 21 6 11 8 10 12.8
在窗口最长逗留时间(min) 26 43 15 28 27 21 32
平均等待时间(min) 4 17 2 7 4 5 7.8
最长等待时间(min) 22 38 11 24 24 17 27.2
窗口空闲时间百分比 9.42% 1.94% 10.70% 8.28% 13.46% 10.90% 10.94%
虽然时间上略有增长,但是仍在可以接受的范围内,同时窗口工作率也很正常,处在一个比较繁忙的状态,不冷清也没有忙到爆。所以在商家有利可图即能有更大贸易量的情况下,多开窗口,是一种对客户与商家双赢的局面。
需要说明的是,上述的模拟是一种单服务台数学模型,这种情况下的蒙特·卡洛方法相对不那么复杂,可以很轻松的模拟出近似的结果,提供一个大概的判断。
注: 蒙特·卡洛方法是一种随机模拟方法,将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。在经济学、计算物理学上应用广泛。近似找π更是小菜,蒲丰投针差不多就是它的前身。想出这个方法的人大家都认识,叫冯·牛·诺伊曼。而打酱油的蒙特·卡洛,它不是人,而是一个赌城。赌博什么的,那基本就是概率统计的游戏咯。
声明:文章转自果壳网,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











