上一次图解微文中,介绍了向量的概念以及加法和数乘运算,这样就构成了线性空间。
一、基底
在二维线性空间中,只要用两个特殊的向量就可以来用定位(表示)出任意向量:
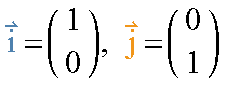
图1
空间中的任何向量都是可以通过缩放这两个向量再相加表示出来。现在想象,譬如向量(3,2)就是沿着 i 的方向拉伸3倍,再沿着j方向拉伸2倍的向量相加结果。

图2
这样特殊的向量称之为基(Basis,或基底),任何二维向量都可以由这两个向量的线性组合表示出来,其中a, b为标量。
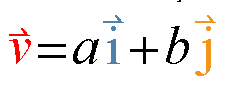
图3
观察下面动图显示,当两个标量自由变化,通过向量加法与向量数乘这两者基础运算,就能获得所有二维中可能的向量:
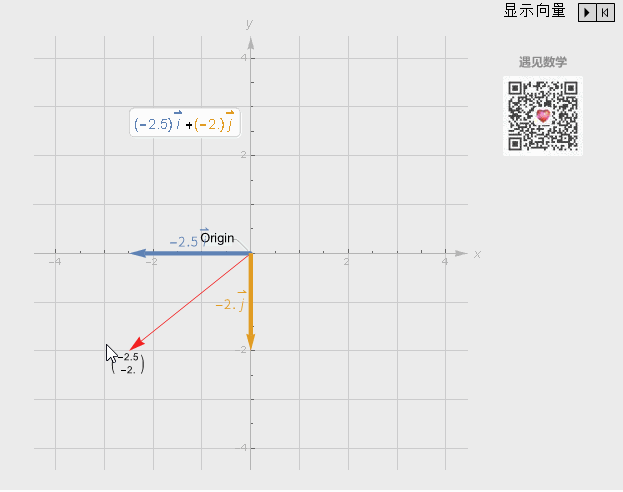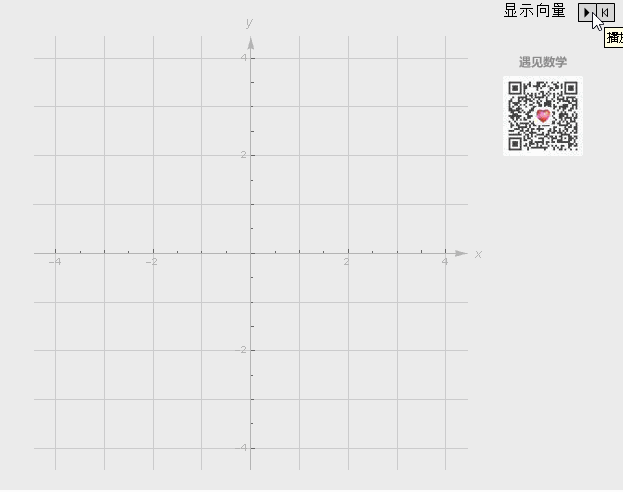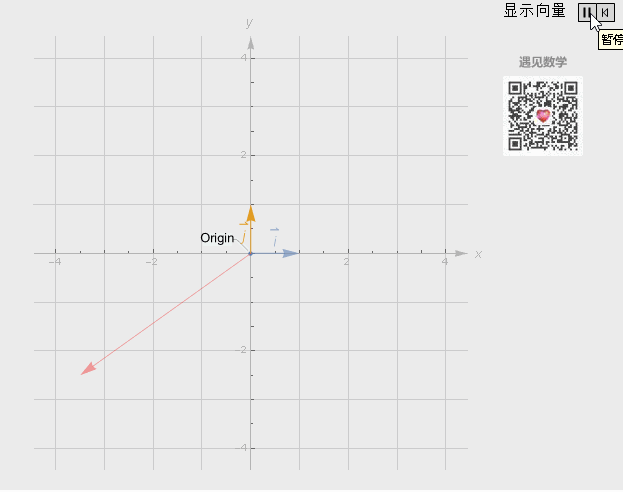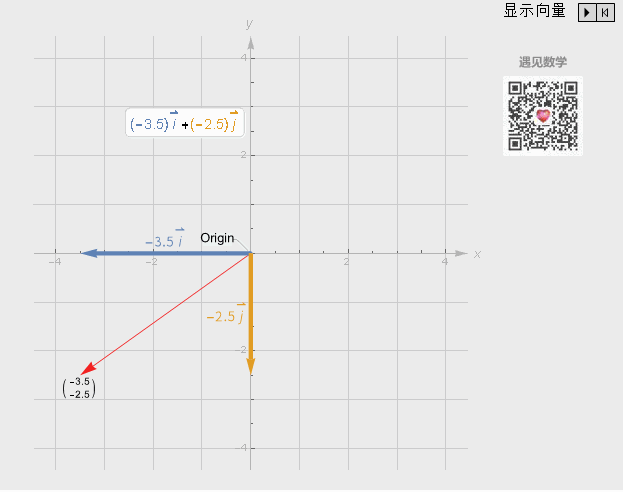
图4
基底的选取有各种各样的方式,但不同的选取可能会有3种情况,观察下面动图中选取 i 和 j 作为基底出现:
● 也可以线性表示出空间中任意的二维向量;
● 如果两个向量恰好共线时候,所产生的向量的终点被限制在一条过原点的直线上;
● 两个向量都是零向量,其组合向量是零向量。
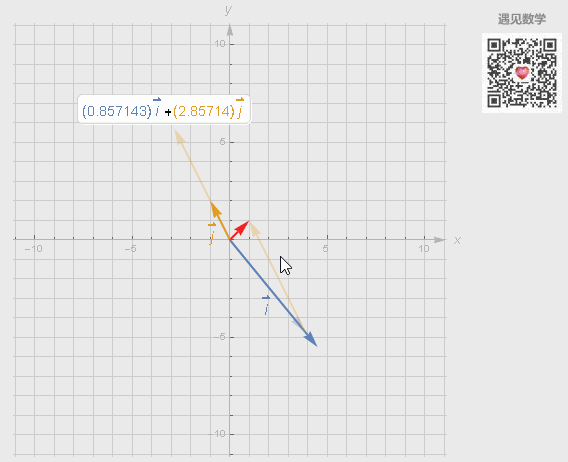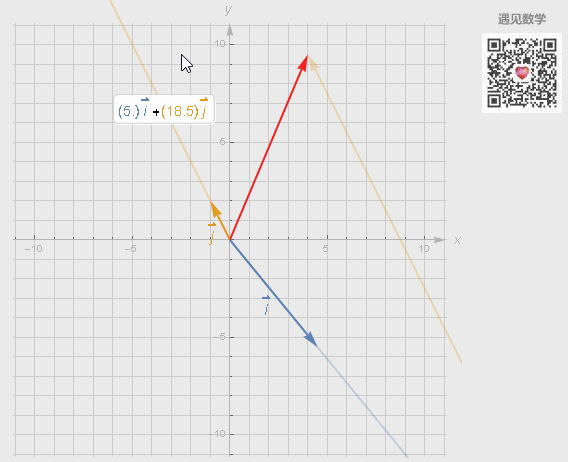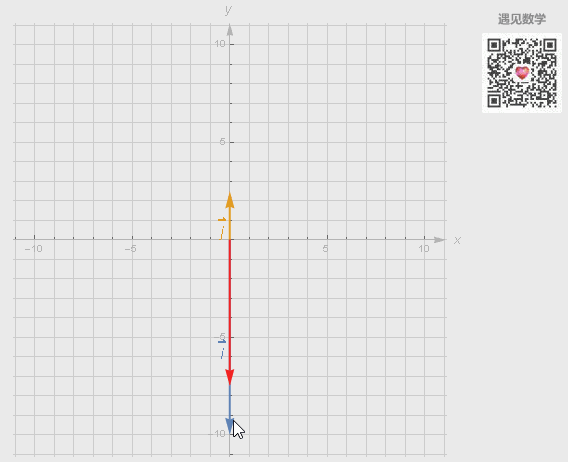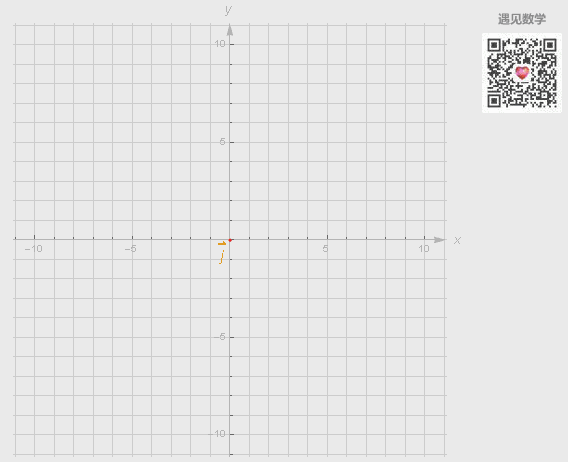
图5
所有由向量i和j线性组合而获得所有可能的向量集合,称之为两个向量张成的空间(Span)。
用上面的图形来说明:对大部分二维向量来说,两个向量所张成的空间是所有二维向量的集合,可以称之为基底;但当共线时,张成的空间就是一条直线,不能构成基底。
二、三维空间的基底
再来看看三维空间中的两个方向不同的向量所张成的空间就是两者所有的线性组合,张成了一个过原点的平面。
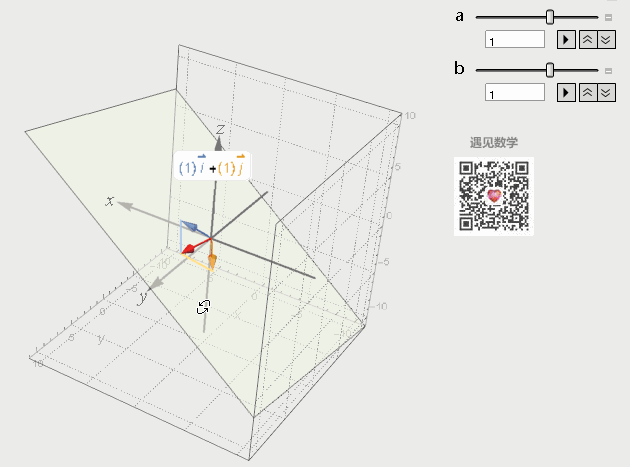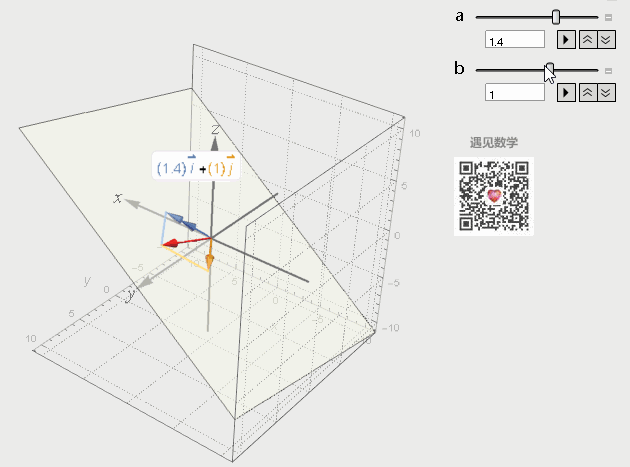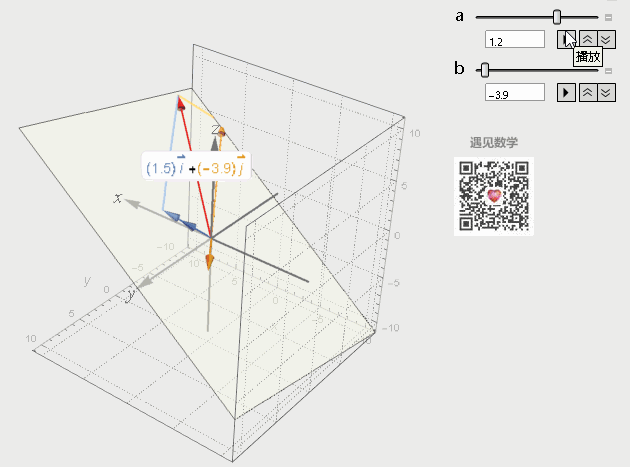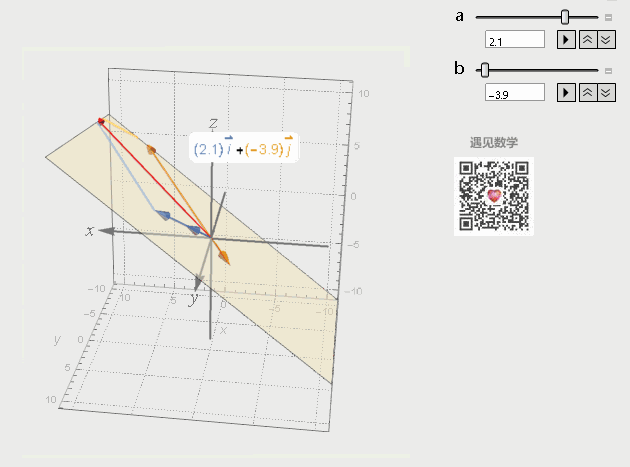
图6
如果在加上第三个向量,那么线性组合为下面的形式:
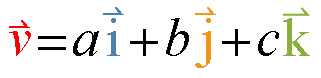
图7
对三个基底向量分别进行缩放,然后把结果相加,而这三个向量所有可能的线性组合构成了他们张成的空间:
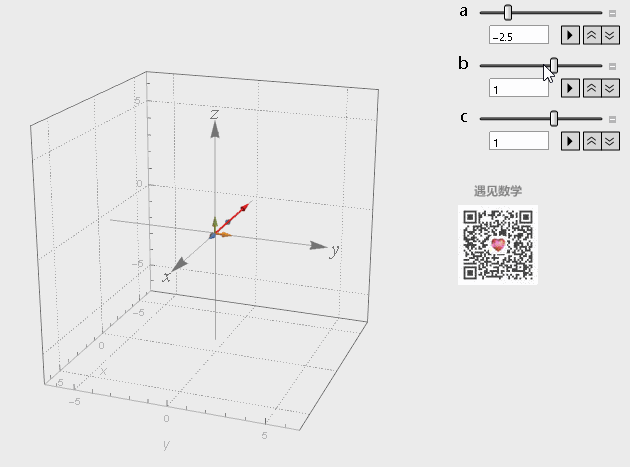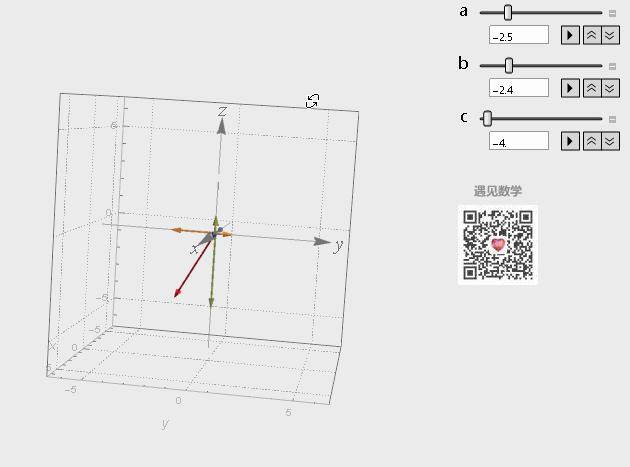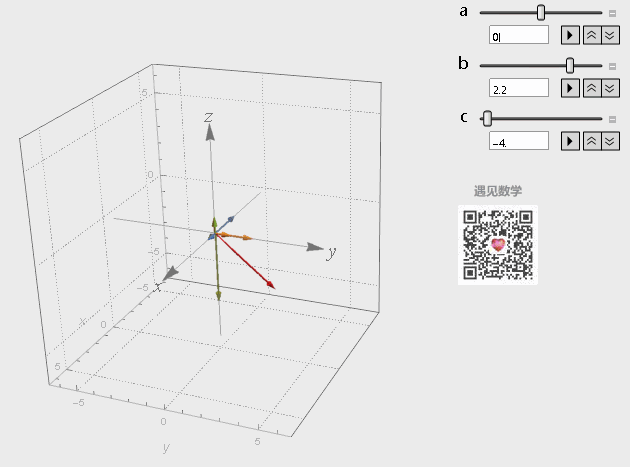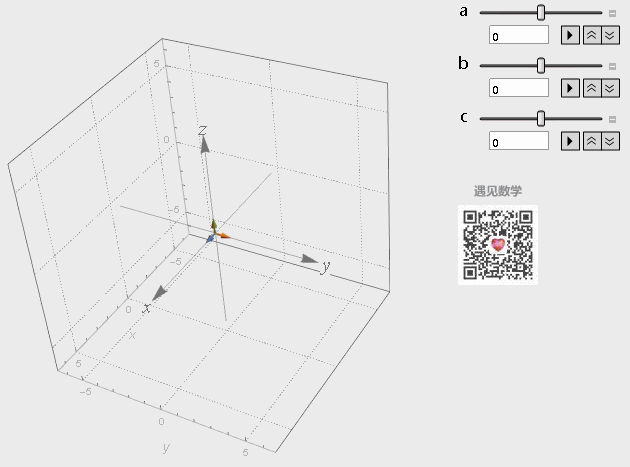
图8
三、线性相关
考虑三维中第三个向量已经落在前两个向量所张成的平面之中,那么就可以被这两个向量线性表示;或者二维中两个向量共线,那么可以由另一个线性表示出来。

图9
这种情况称之为线性相关(Linearly Dependent),也就是说存在有向量对张成空间而言上多余的,即便删除掉也不会对张成的空间有任何影响。反之称为线性无关,也就是没有任何向量可以由其他向量经过线性组合表示出来,每个向量对所张成的空间都做出了“贡献”。
上面就是图解线性代数例子。好了,现在让我们在下一篇的中继续探索。因为本人水平有限,疏忽错误在所难免,希望各位老师和朋友多提宝贵意见,帮助我改进这个系列,感谢关注!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











