这次我们来看看三个方程式,三个未知数的方程组解(即平面方程组)的情况。其中每一个方程可以看做代表了三维空间中的一个平面,而方程组的解集就可能是空间中的一部分:无解,一个交点,一条直线或一个平面;
一、方程组唯一解的情况
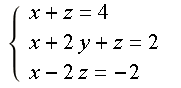
从行视图来理解就是三个平面相交于一点:
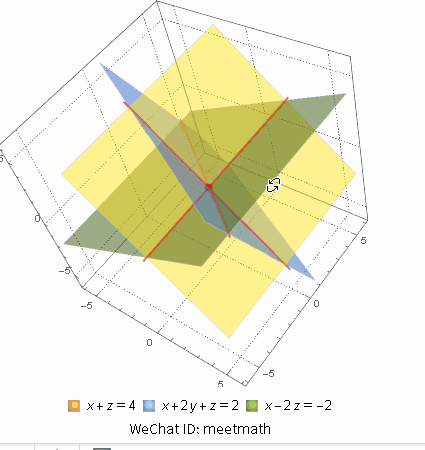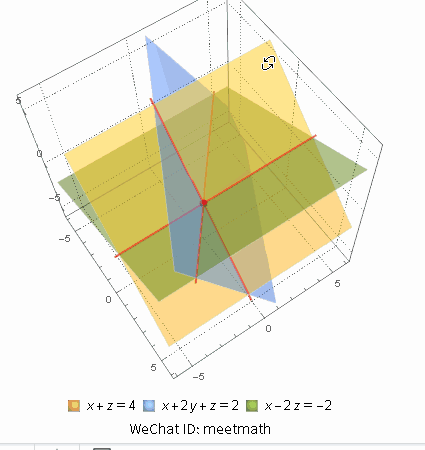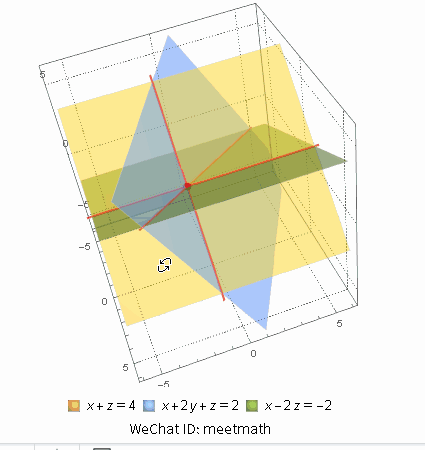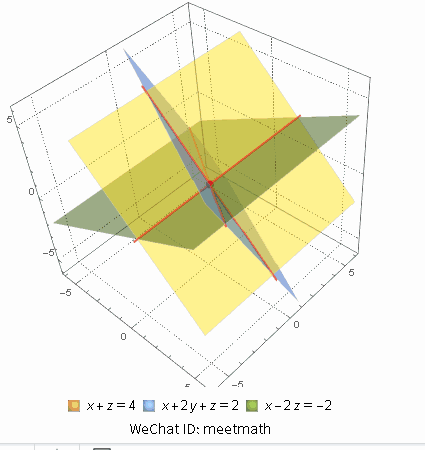
图1
如果从矩阵变换的角度来理解的话,请观察下图:
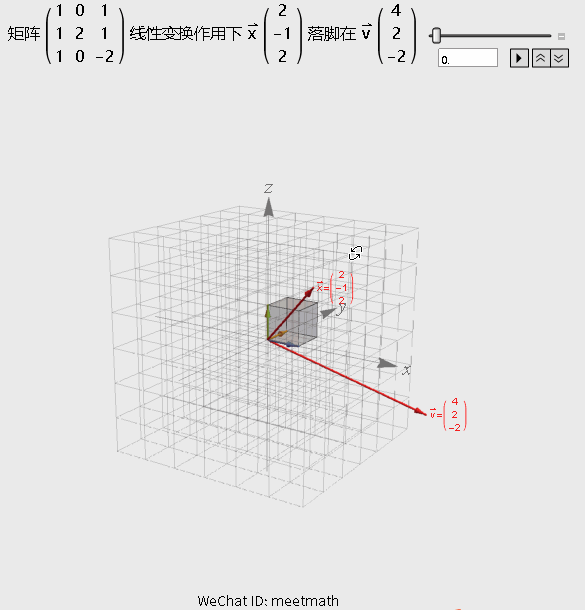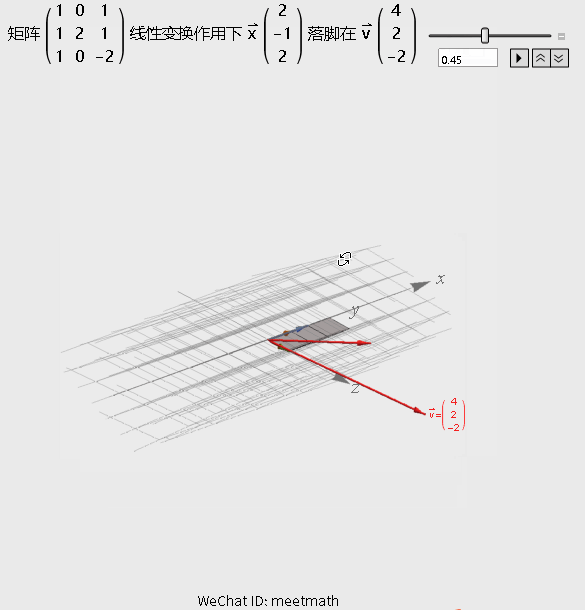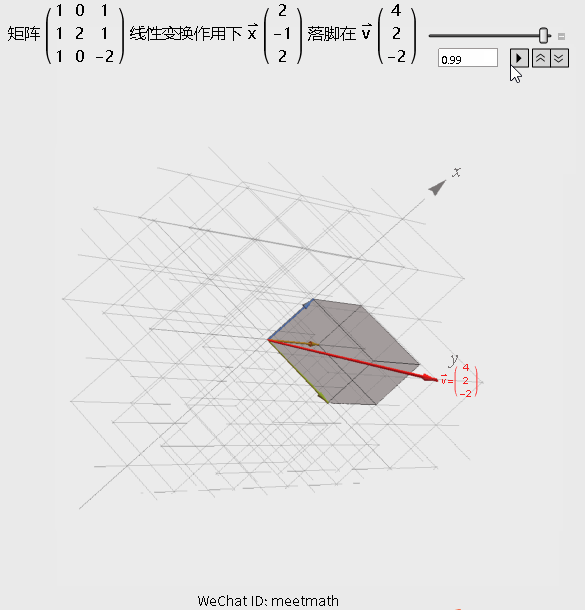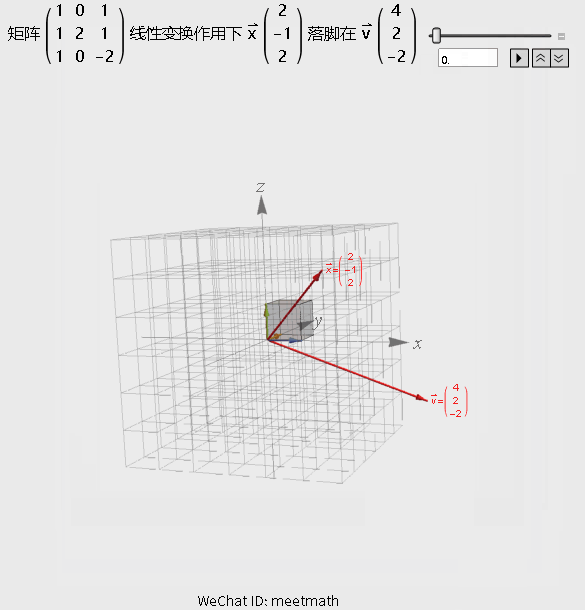
图2
观察要点:
● 经过矩阵变换后,仍是三维空间;
● 解向量x在变换后,与向量v重合;
● 向量v可以被矩阵A的列向量线性表出,也就是落在列空间内。
二、方程组无解
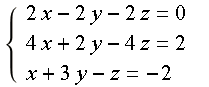
其中三个平面交线相互平行,不会有任何共同的交点,所以无解:

图3
如果从矩阵变换的角度来理解的话,请观察下图:
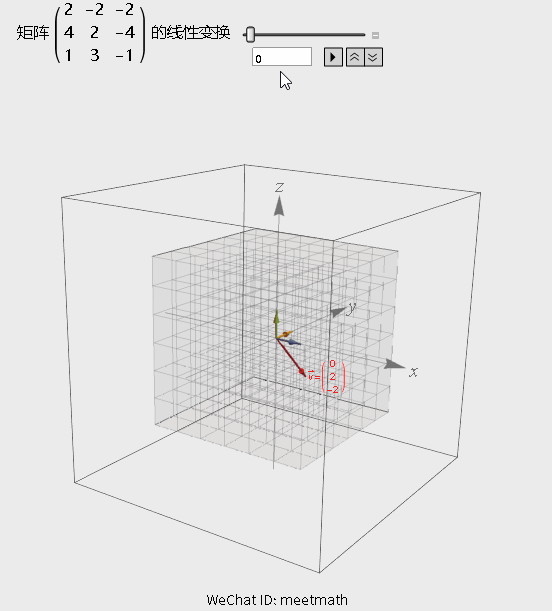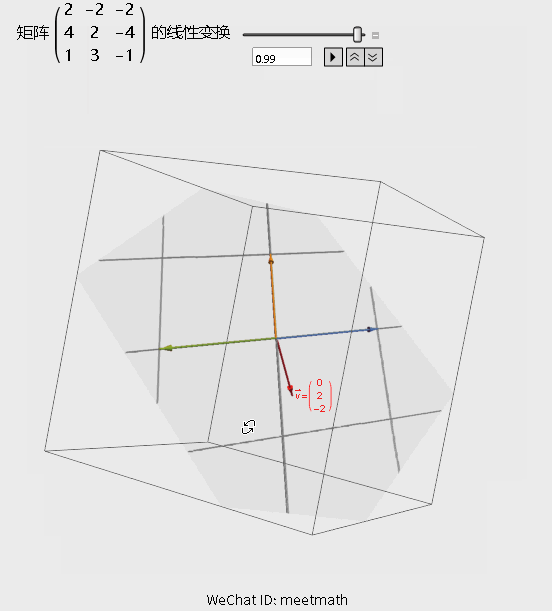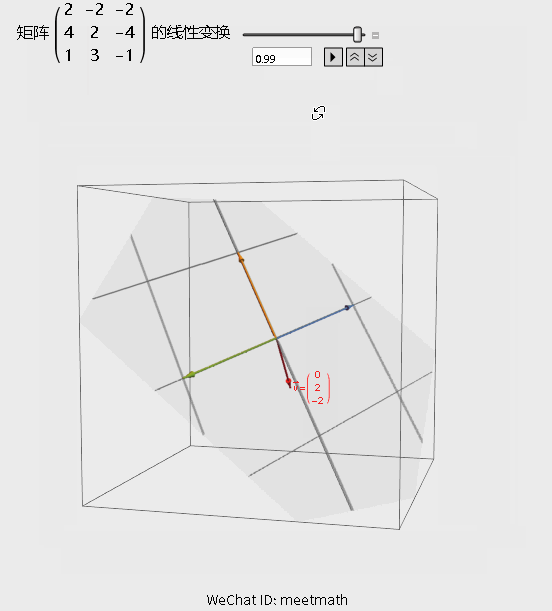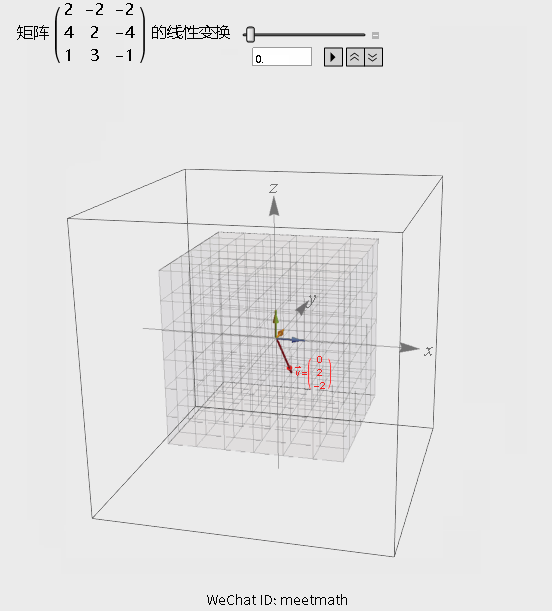
图4
观察要点:
● 经过矩阵变换后,空间被压缩为平面;
● 由于向量v在平面之外,所以无法被矩阵的列向量线性表出,落在列空间之外。
三、方程组有无穷解 - 解集为一条直线
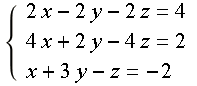
三个平面相交于一条直线:
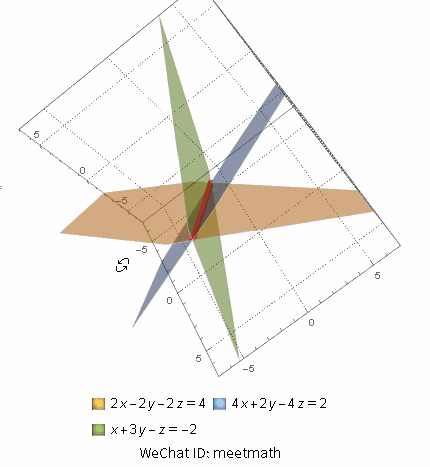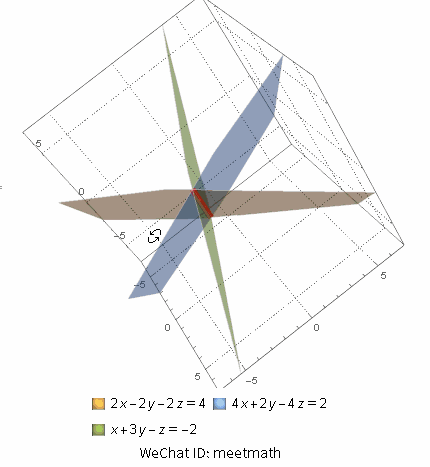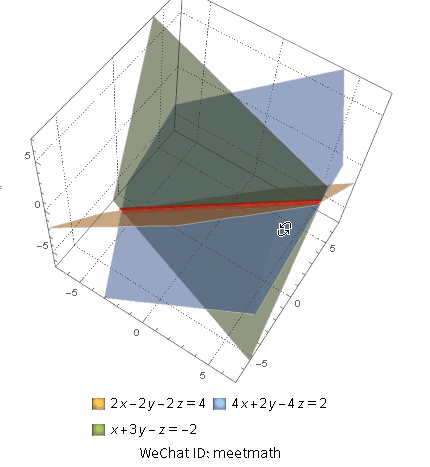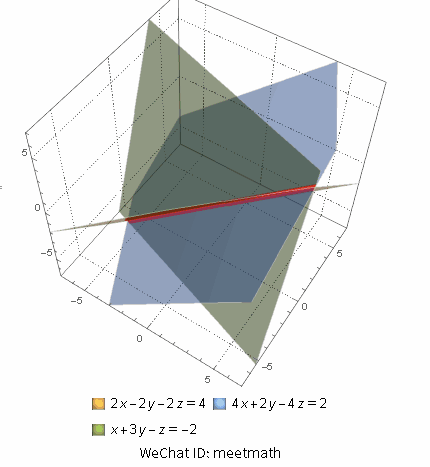
图5
如果从矩阵变换的角度来理解的话,请观察下图:
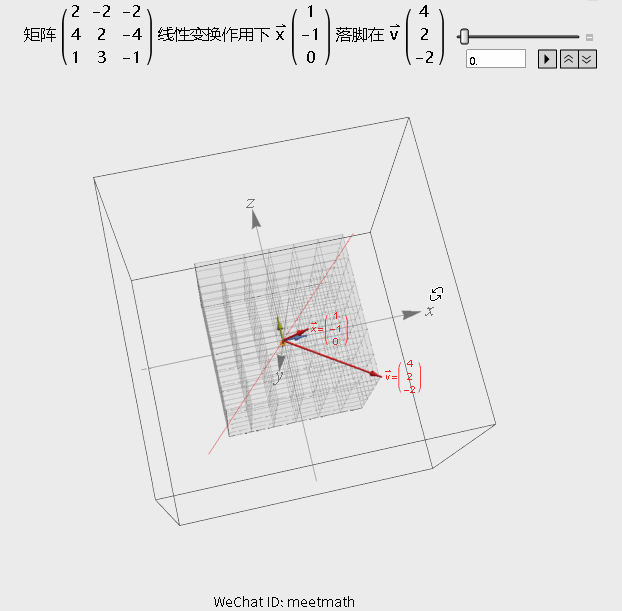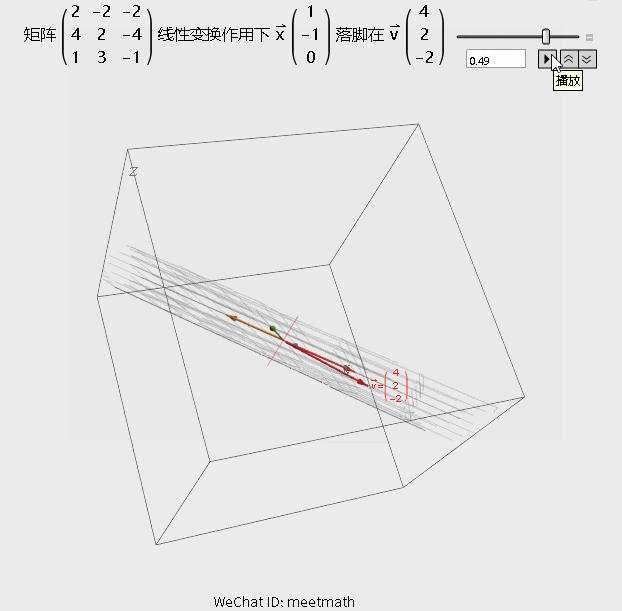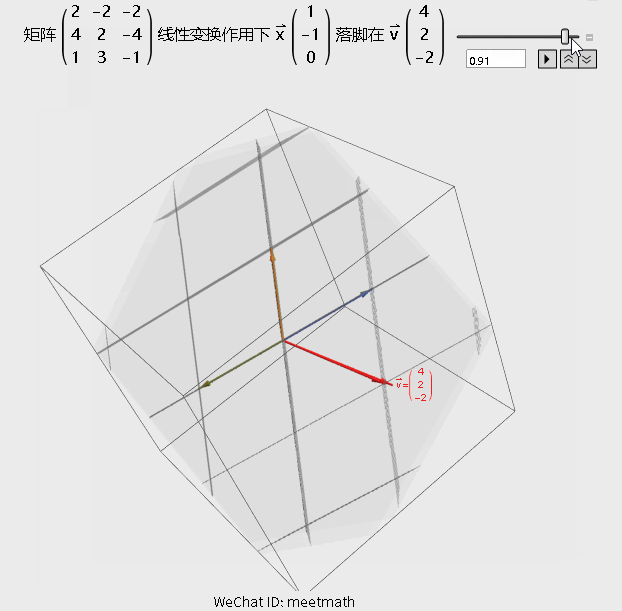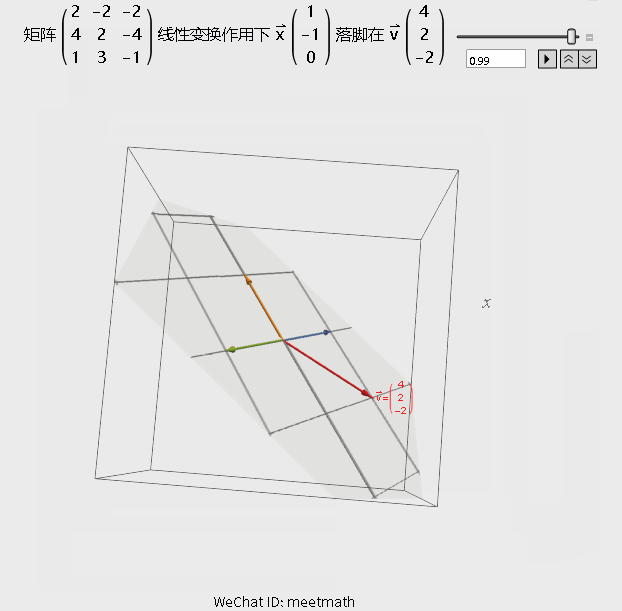
图6
观察要点:
● 空间经过变换被压缩为平面;
● 行列式为0,即逆矩阵不存在,但解仍然存在,因为v就在该平面上,即在列空间内;
● 图形中红色细线上的所有向量在变换后都被压缩到原点,成为零向量。
方程的通解为特解+零空间上解所有的线性组合:
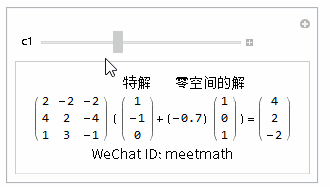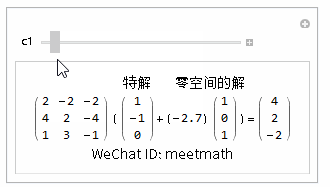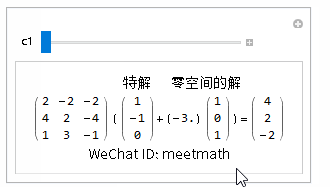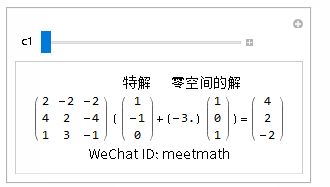
图7
四、方程组无穷解 - 解集为一个平面
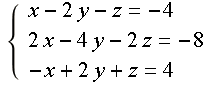
三个平面实为一个平面:
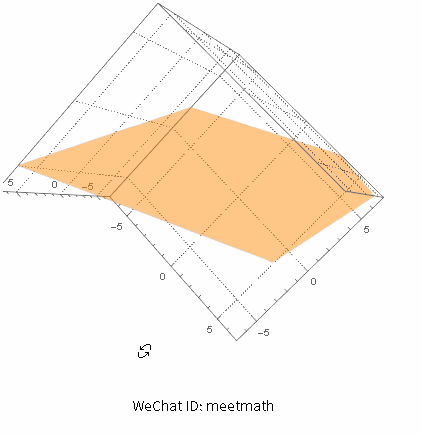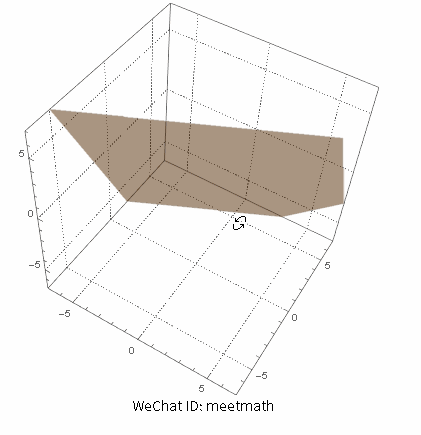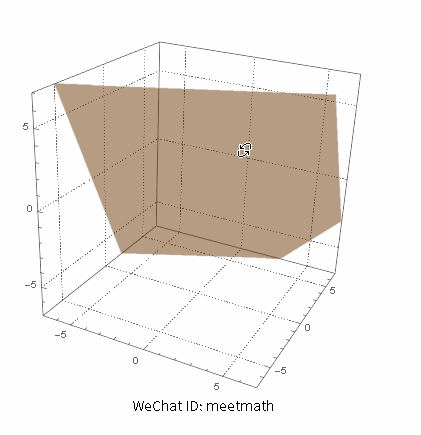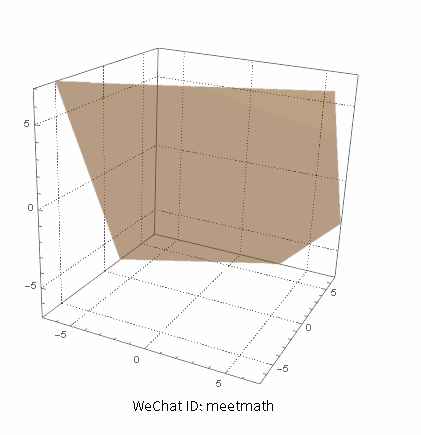
图8
如果从矩阵变换的角度来理解的话,请观察下图:
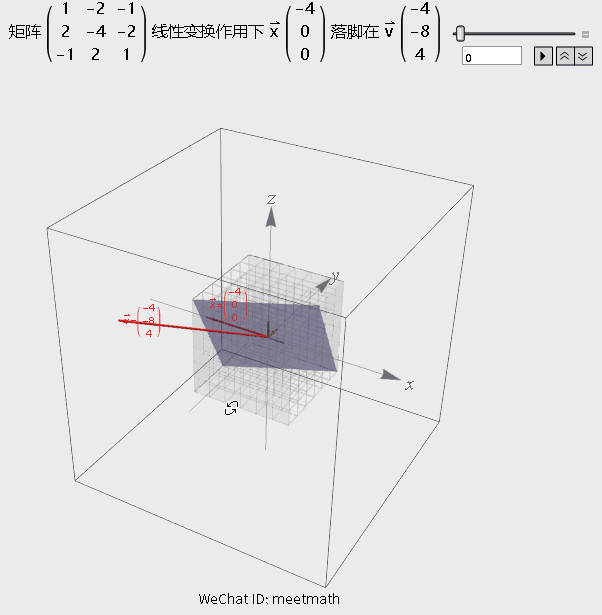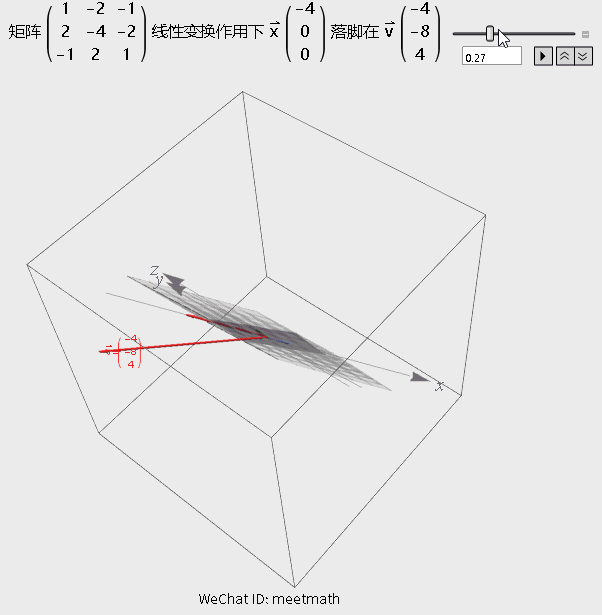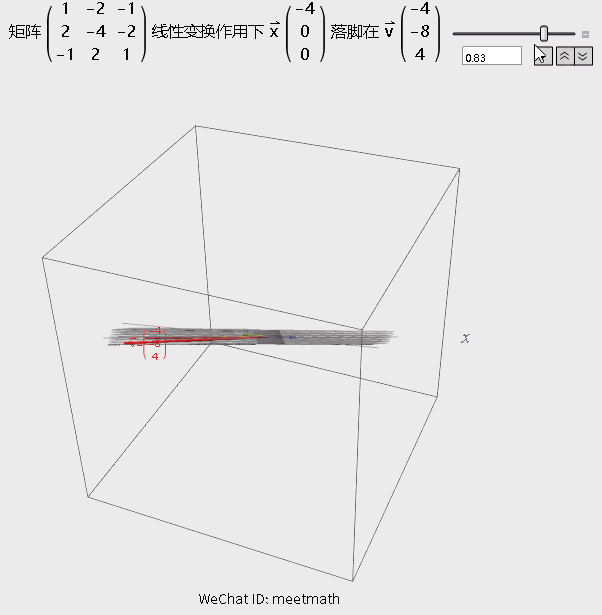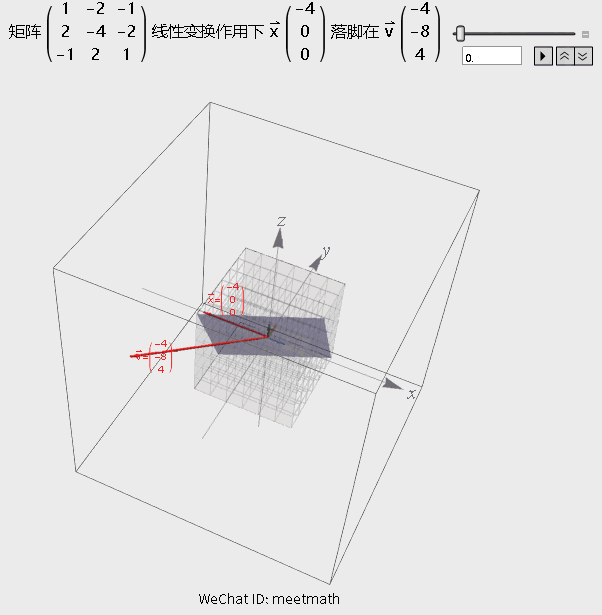
图9
观察要点:
● 矩阵变换将空间压缩为一条直线;
● 行列式为0,即逆矩阵不存在,但解仍然存在,因为v刚好就在这条直线上,还在列空间内;
● 图形中浅蓝色平面上的所有向量在变换后都被压缩到原点, 成为零向量。
方程的通解为特解+零空间上解所有的线性组合:
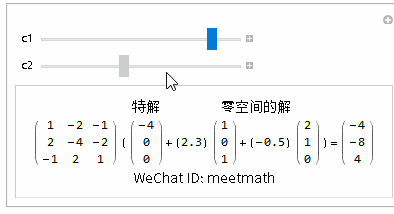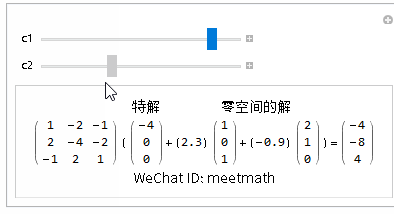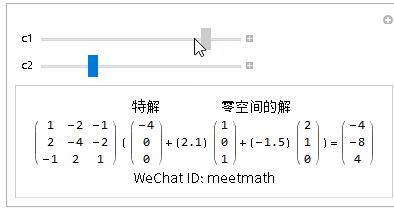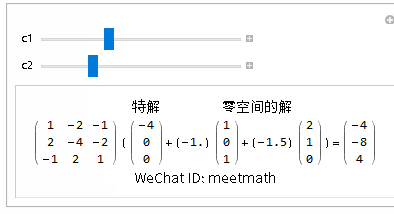
图10
这一次我们从行视图和列视图的几何角度理解线性方程组:每个方程组都有一个线性变换与之联系;当逆变换存在时,就能用逆变换来求解方程组的解;逆变换不存在时,行列式为0,就需要考察向量v是否落在列空间内了。
上面就是本次图解线性代数所回顾的知识点。好了,现在让我们在下一篇的中再见!因为本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











