我们来做一个简短的回顾。
矩阵乘法可以理解为一个特定的线性变换,矩阵的列向量相当基向量i: (1,0)和j: (0,1)经过变换过后的到达向量。
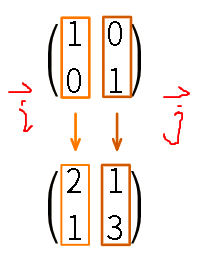
图1
空间变换后的任何向量都可以由矩阵A的列向量线性表出,而这些所有可能的结果,也就是矩阵的列所张成的列空间(Column Space)。
原先的空间经过这样2x2矩阵A线性变换后的空间可能会三种情况:
● 还是平面——仍是二维空间;
● 被压缩为一条线——变成了一维;
● 被压缩到原点——零维。
在数学专业的词汇来表示线性变换后空间的维数,称之为矩阵的秩( Rank )。换句话说,列空间就是矩阵的列所张成的空间。所以矩阵秩的另一种定义可以说是列空间的维数。经过变换后被压缩到原点的向量集合,称为矩阵A的“零空间”(Null Space)或“核”(Kernel),记为Null(A)或Ker(A)。
对照上面的三种情况,来分别来观察。
一、变换后仍是平面
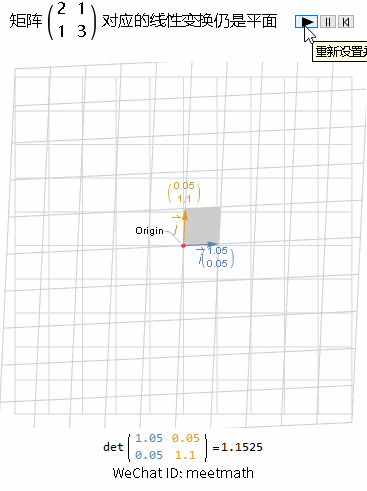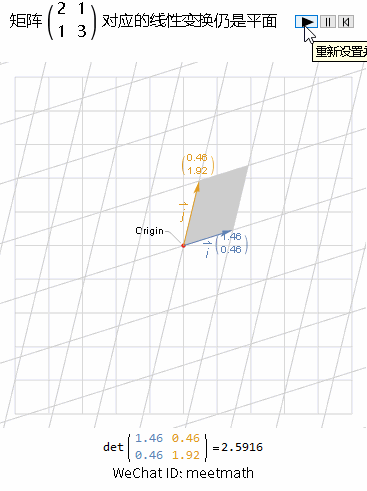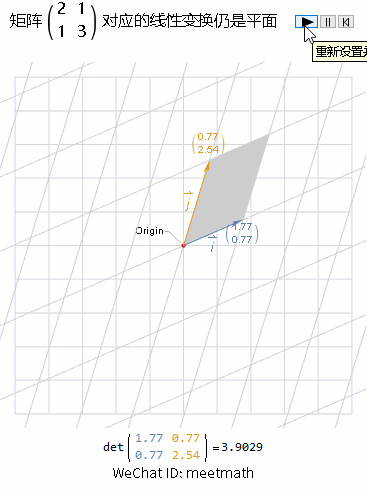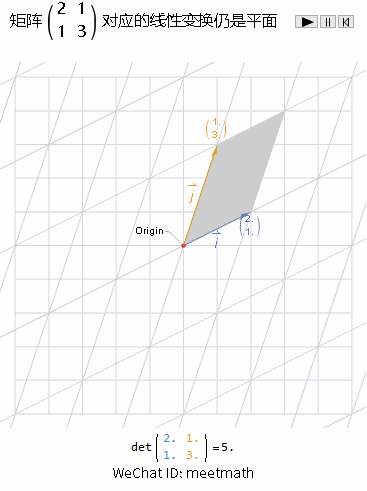
图2
观察要点:
如果经过矩阵A变换后的结果是一个平面,则rank( ) = 2,空间没有被压缩扁平化,因此可逆,称之为非奇异矩阵;
● 这样秩与列数相等,称之为满秩(Full Rank)矩阵。
● 对于满秩矩阵来说,变换后唯一落在原点的就是零向量本身,也就是dim Ker( ) = 0。
二、变换后被压缩为一条直线
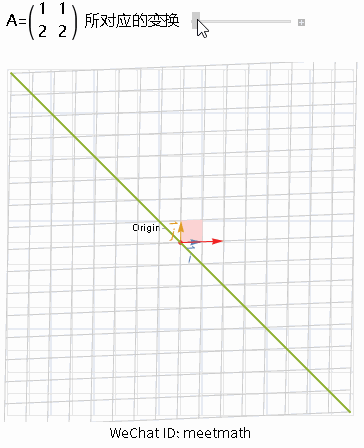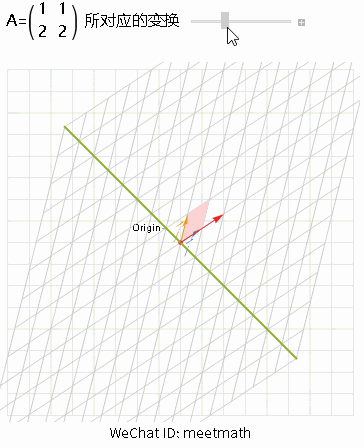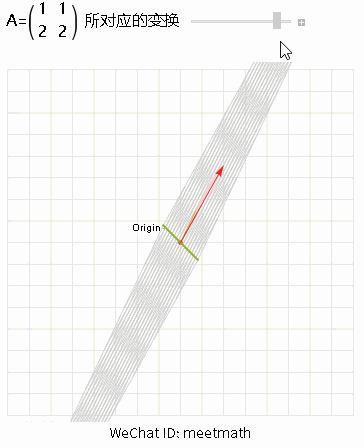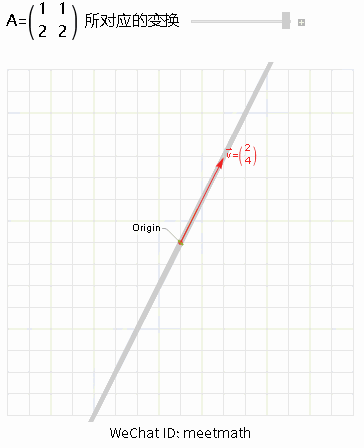
图3
● 当变换的结果是一条直线,该矩阵是一维的,称rank(A) = 1,此时矩阵不可逆,称为奇异矩阵;
● 这样非满秩矩阵,会将空间压缩到更低的一维直线上,也就是由嫩绿色直线上一系列的向量在变换后成为零向量;
● 零空间的维度为1,dim Ker(A) = 1。
三、变换压缩到原点
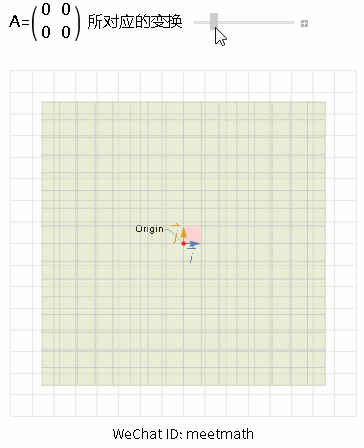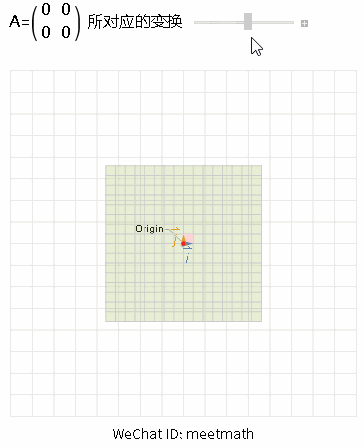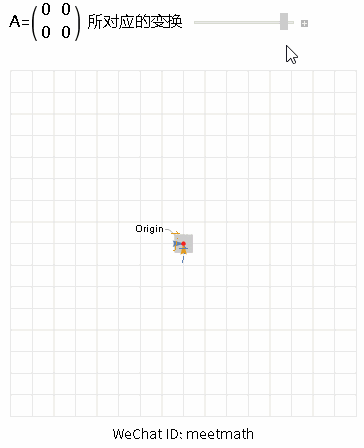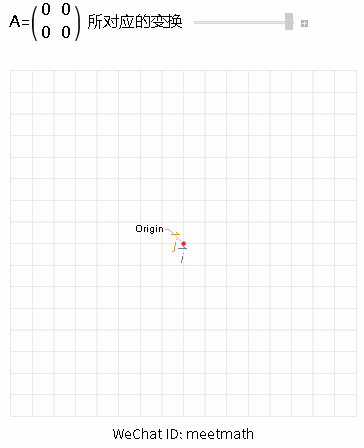
图4
● 当变换的结果是压缩到原点,则该矩阵是零维的,称rank(A) = 0;
● 而零空间维度为2,dim Ker(A) = 2。
四、维数定理
假设A是mxn矩阵(非方阵的情况,下次会介绍),维数定理就是:
dim Ker(A)+rank(A)=n
相信如果理解透彻2x2矩阵的情况,那更高维的矩阵也就清楚了。
上面就是本次图解线性代数所回顾的知识点。好了,现在让我们在下一篇的中再见!
因为本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











