图解高等数学系列是以动图的形式将的数学知识点展示出来。希望该系列能够帮助同学们更快,更加深地理解某些较为相关的概念。
因为本人水平有限,疏忽错误在所难免,所以还请各位老师和朋友不吝赐教,多提宝贵意见,帮助我改进这个系列,先感谢感谢啦!
上一次提到过向量是指一个既有方向(direction)又有大小(magnitue)的量,这次看看向量的点积,叉积和三重积。
一、向量的点积(Dot Product)
点积(dot product;scalar product,也称为数量积)。a.b=|a| |b| cos(θ)
点积其中一个非常实用之处可以判断两个向量的方向及角度:
● 如果点积返回结果的值为正数,说明这两个向量指向同一个方向;
● 如果返回结果的值为0,这两个向量互相垂直;
● 如果返回的结果为负数,说明这两法向量指向完全相反的方向。
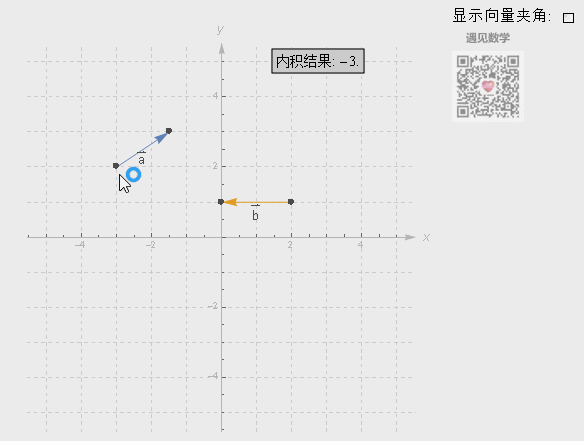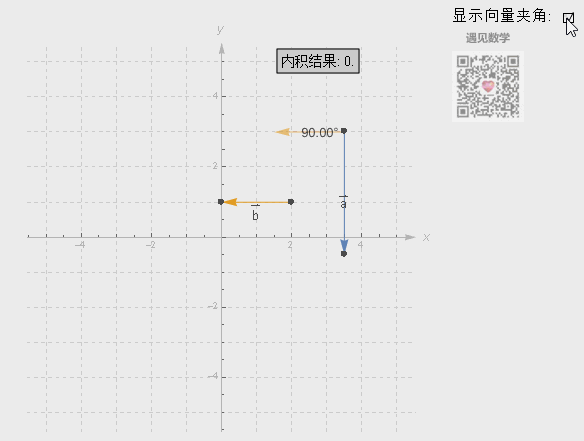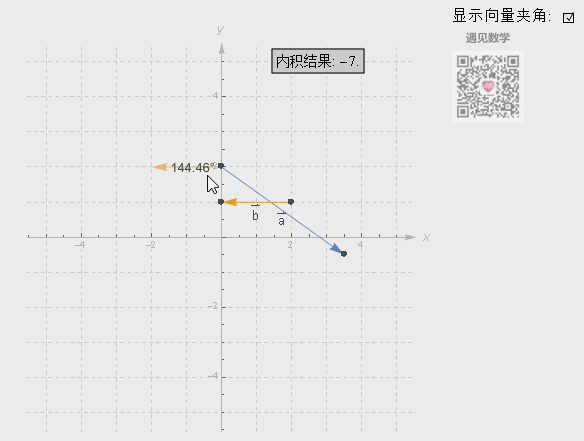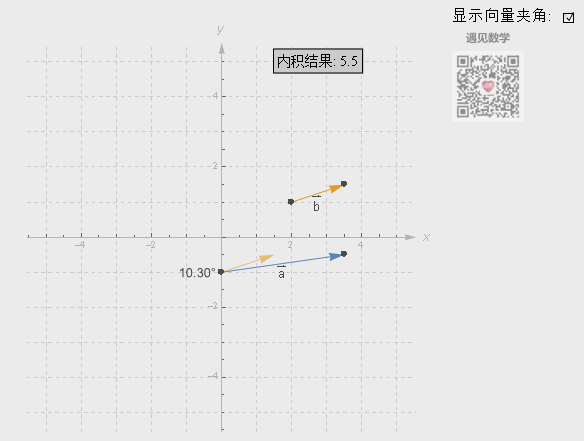
图1
如果我们写成|b| (|a| cos(θ))的形式,可以理解点积的另一个几何意义,向量a在b方向的投影,再乘以b的长度,或者换个角度来看也成,从下图可以理解:
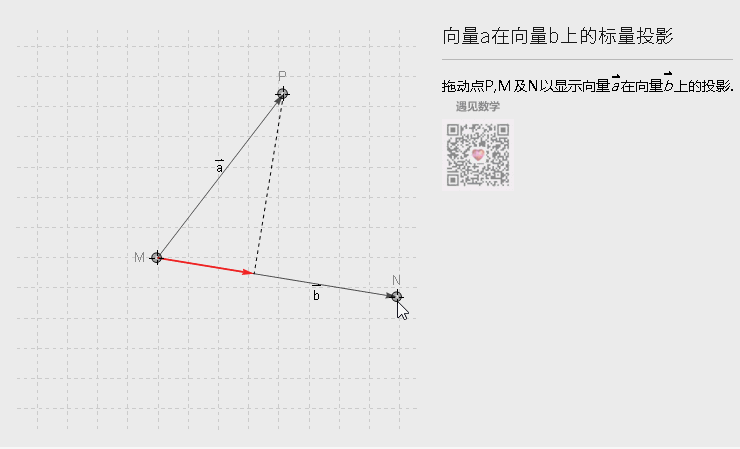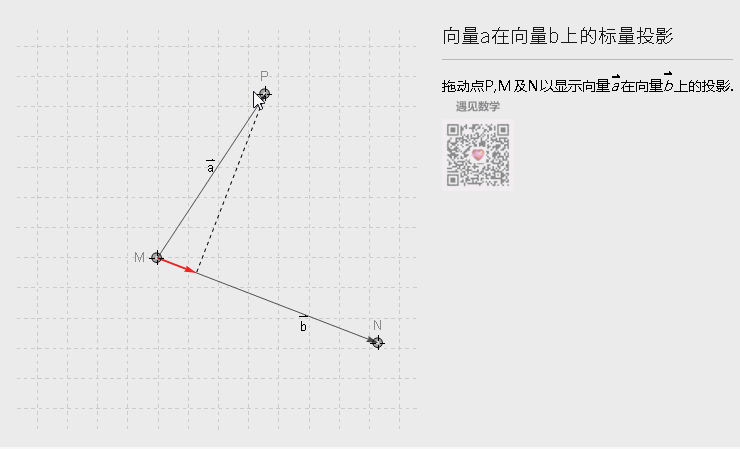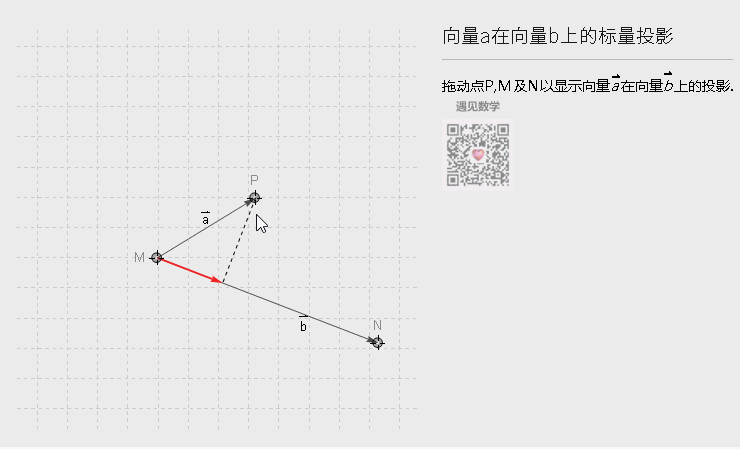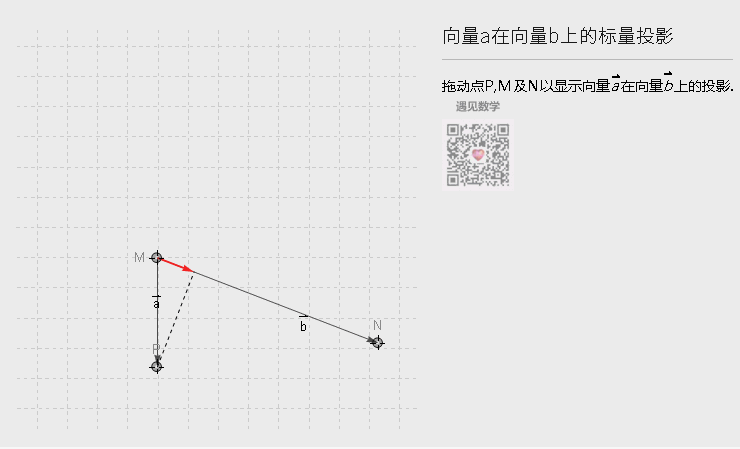
图2
利用点积还可以求点到平面的距离,点在平面上,向量与平面平行问题,这些等到平面时候再进行演示。
二、向量的叉积(Cross Product)
叉积的结果是一个新的向量,这个新向量与前面两个向量垂直,这在计算法线向量时非常有用。另外新向量的长度是|a×b|=|a| |b| sinθ,在这里θ表示两向量之间的夹角,0°≤θ≤180°。
它的几何意义就是由向量a和b定义的平行四边形的面积,其方向满足右手规则。当然如果在求空间中给出三点组成三角形的面积也可以用叉积来算出。
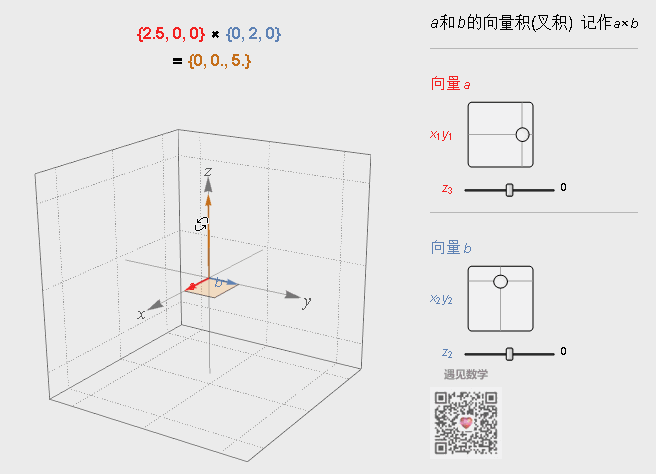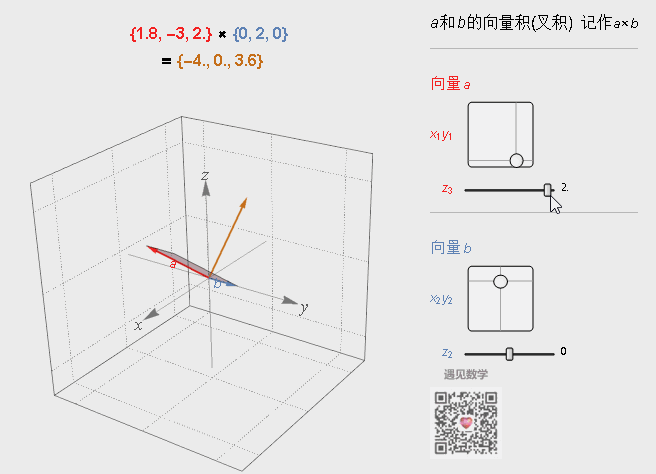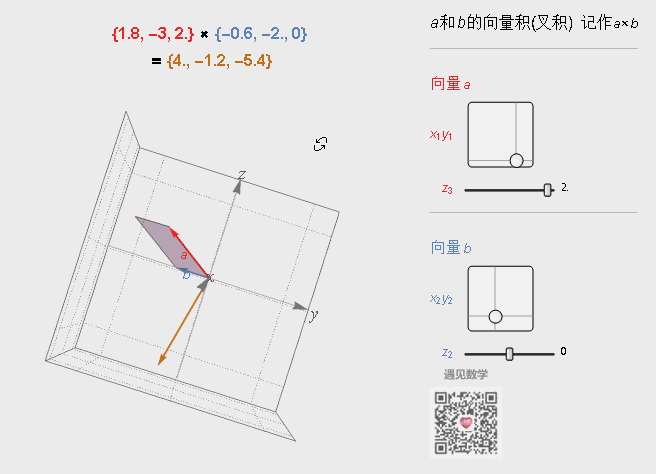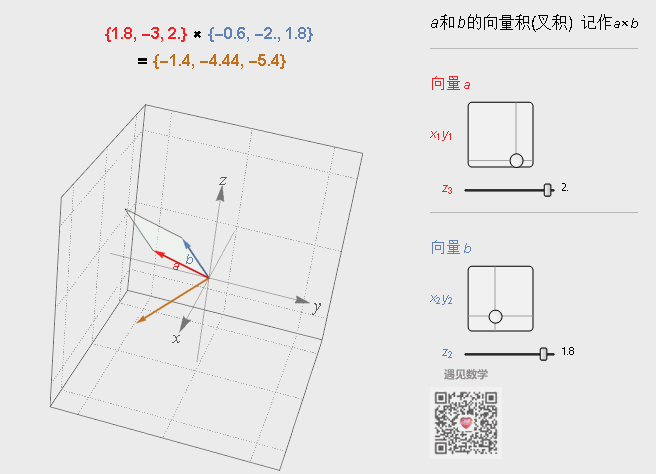
图3
三、向量的三重积(Triple Product)
三重积,又称混合积,是三个向量相乘的结果,就是三个向量中的一个和另两个向量的叉积相乘得到点积。
参照叉乘的几何意义,三重积其实就是由三个向量为棱的平行六面体的体积。
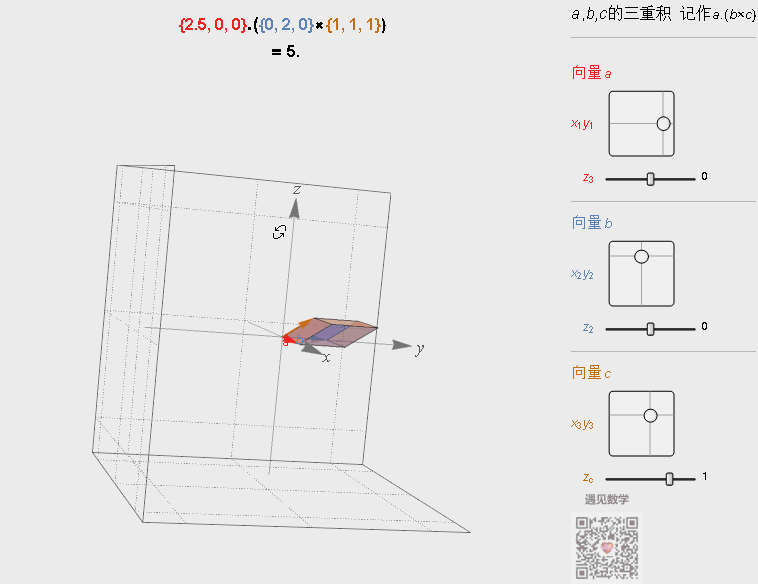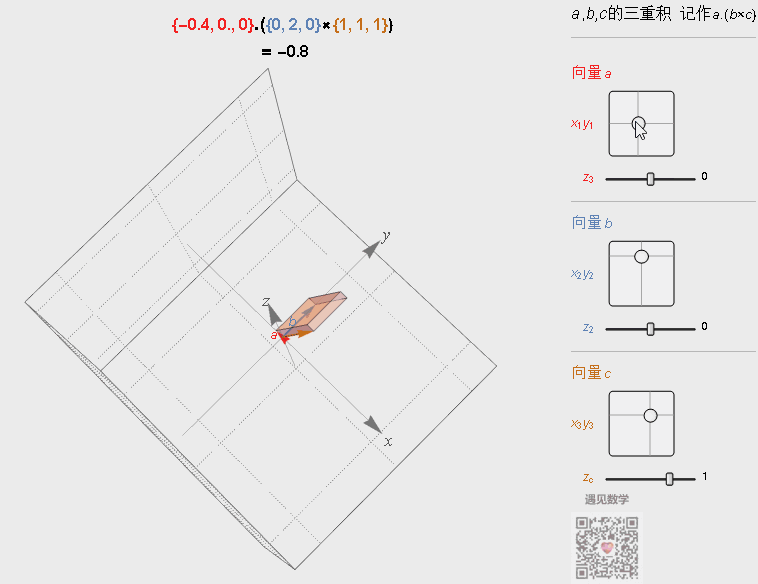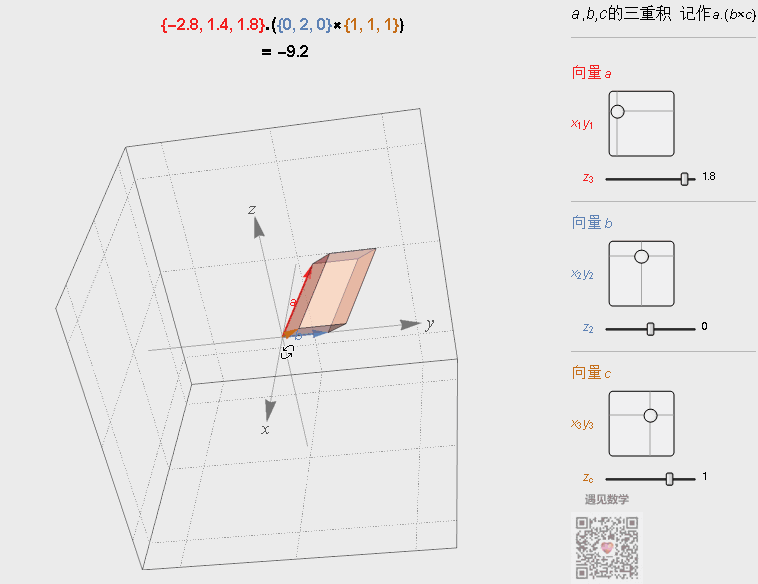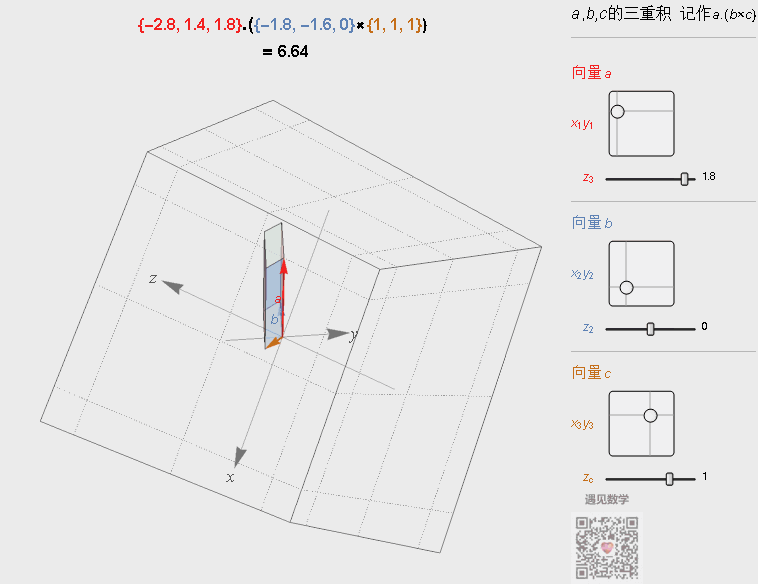
图4
此外,三重积也等于其三个向量组成行列式的值,可以在Wolfram语言中验证Dot[u, Cross[v, w]]⩵Det[{u, v, w}]
上面就是利用Wolfram语言制作的图解高等数学例子。好了,现在让我们在下一篇的中来看一看平面相关的动图。
原创不易,还请多多支持!感谢各位老师和朋友的关注!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











