空间曲线(Space Curves)可看成空间中一个点运动的轨迹。在三维空间R3的直角坐标系中,点的运动可表示为一组参数方程:
x=x(t)
y=y(t)
z=z(t),其中t为参数。
一、圆柱螺旋线
圆柱螺旋线的参数方程如下图所示,绘制的命令ParametricPlot3D[{Sin[u], Cos[u], u/6}, {u, 0, 20}]
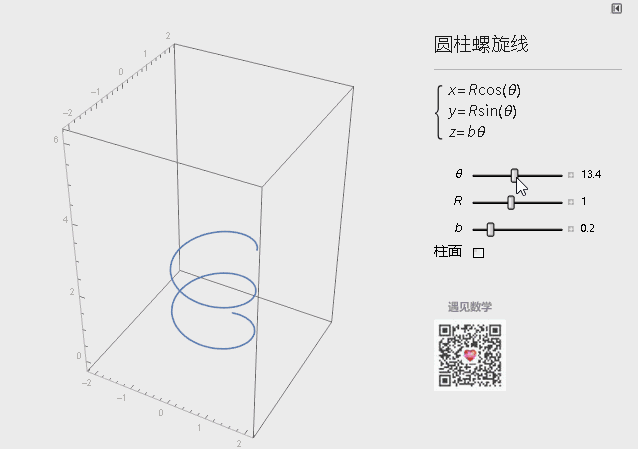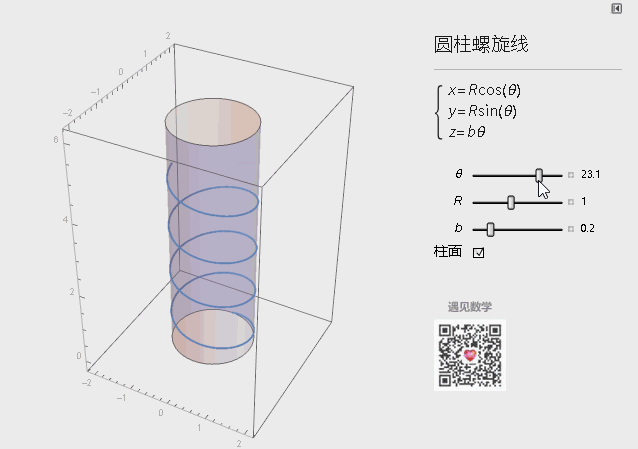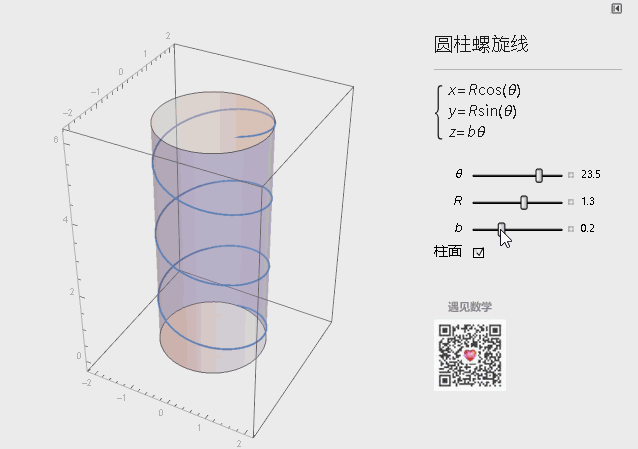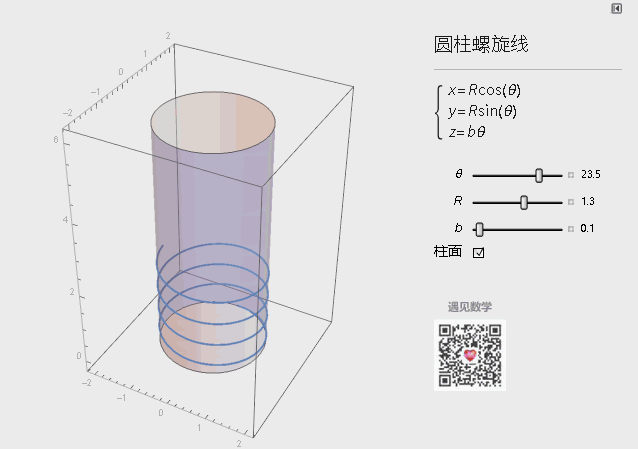
图1
可以参看它的三视图:
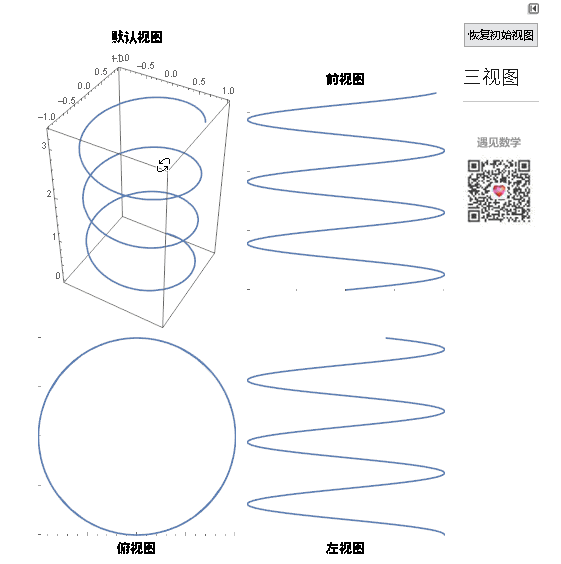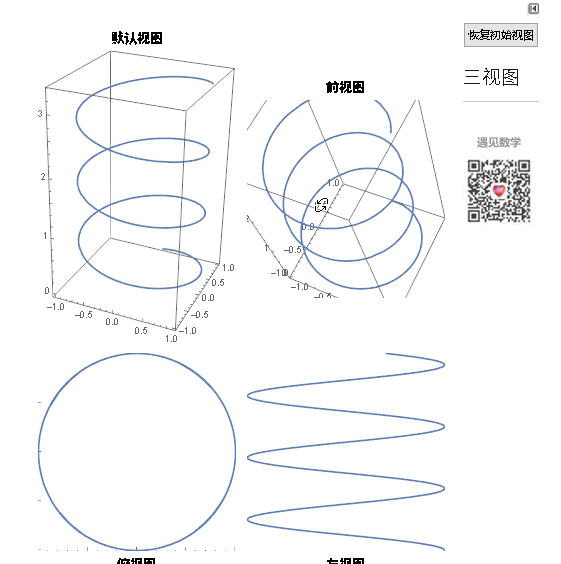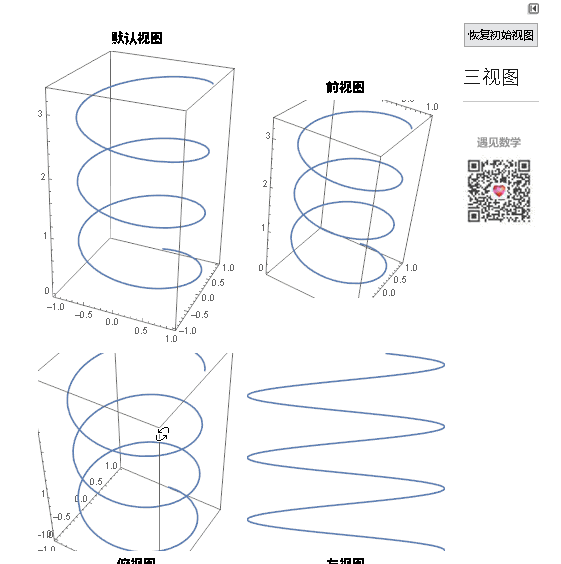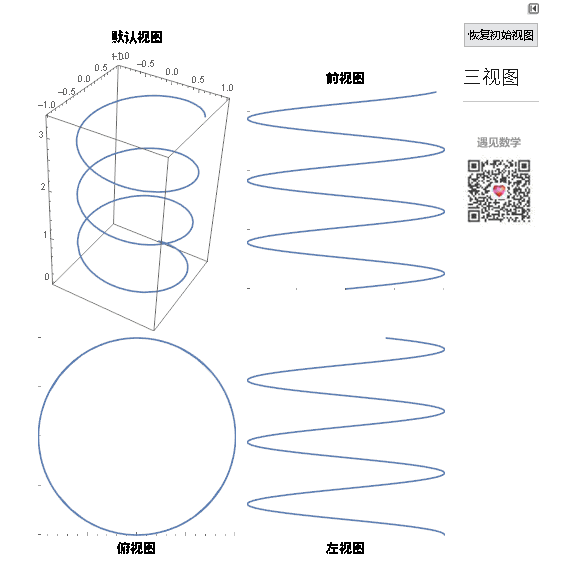
图2
二、空间曲线的一般方程
空间曲线可视为两曲面的交线,下面看两个例子以及相应的三视图:
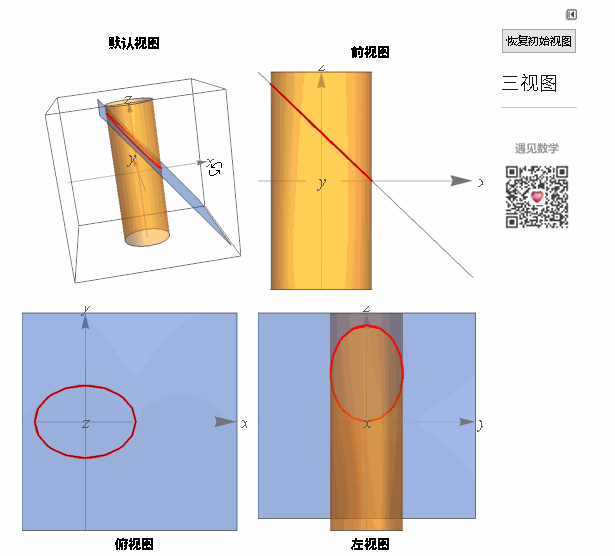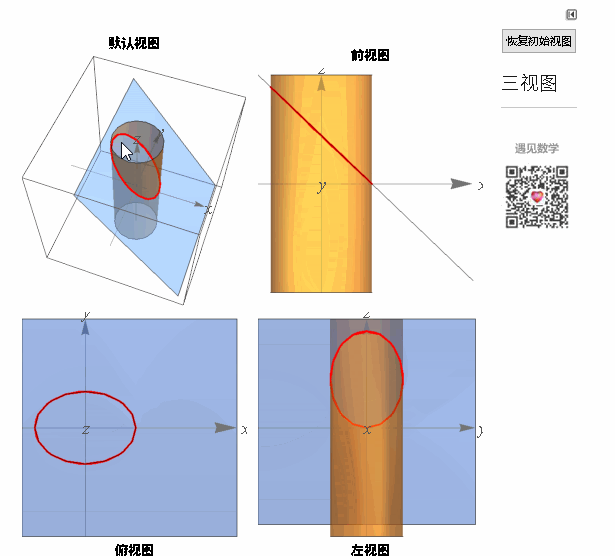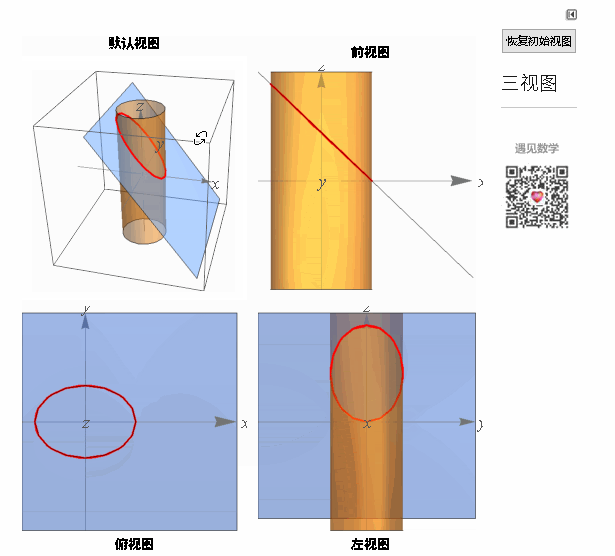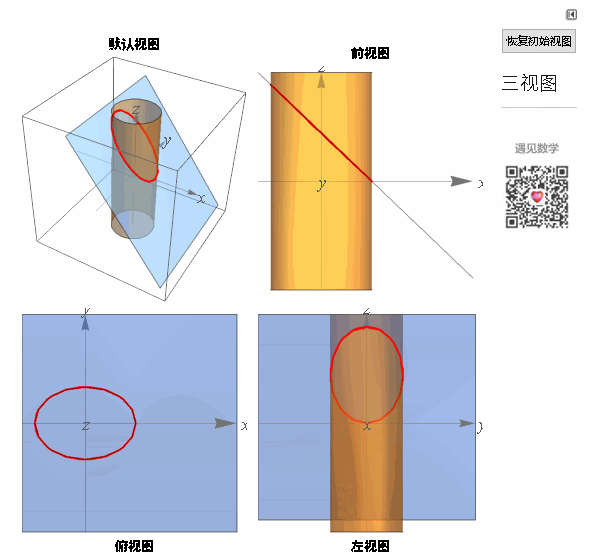
图3
两个圆相交相交的曲线:
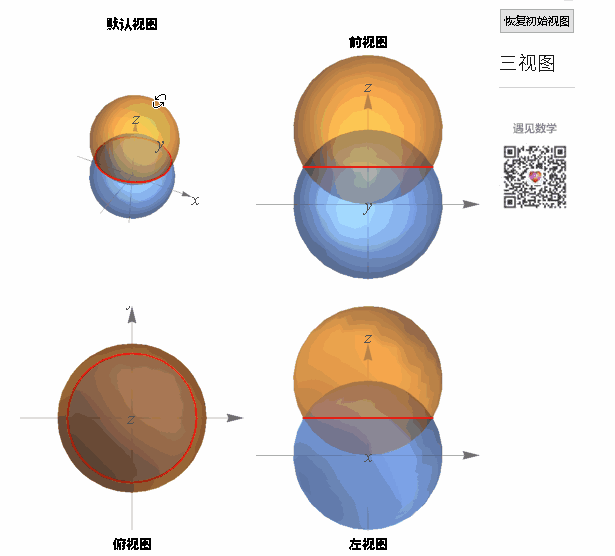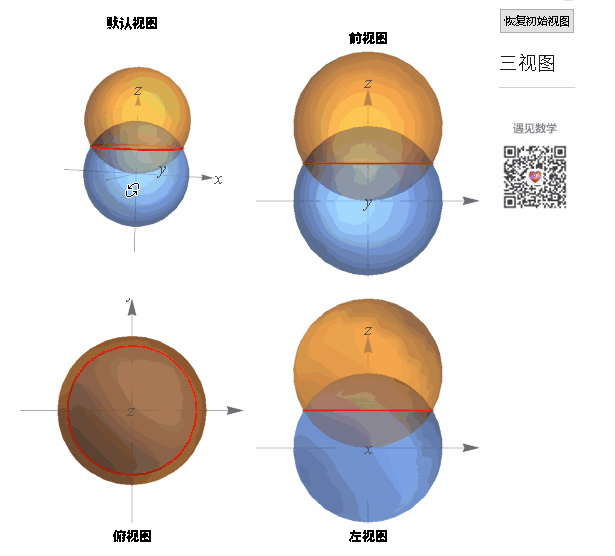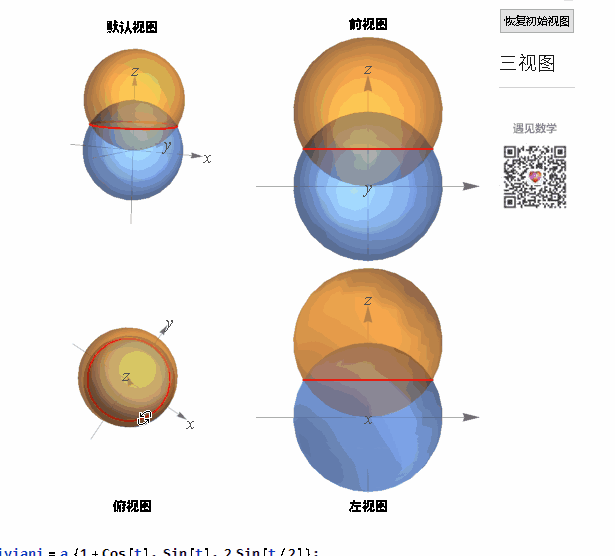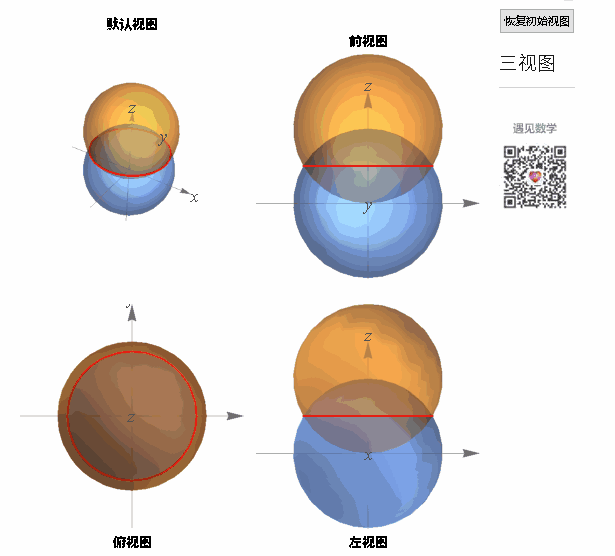
图4
三、旋转单叶双曲面
双曲抛物面是二次曲线里最为复杂曲线。
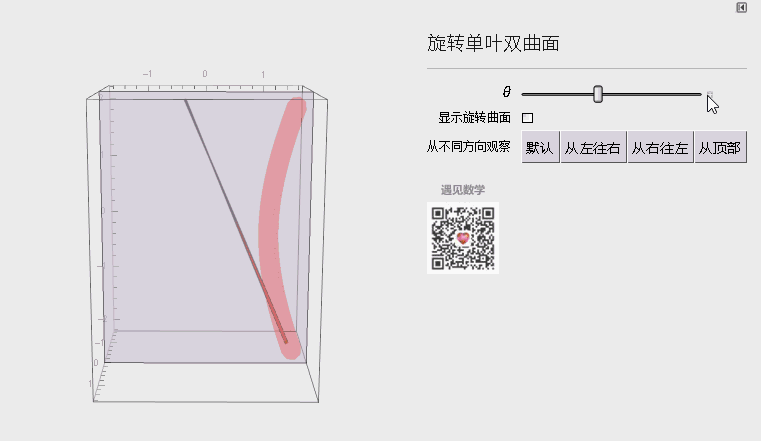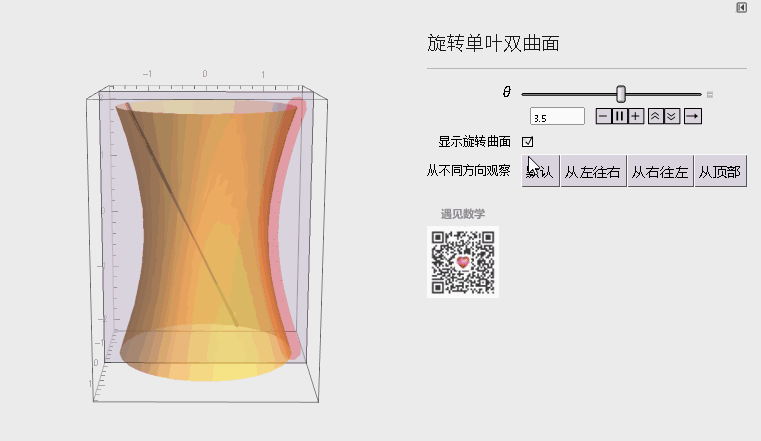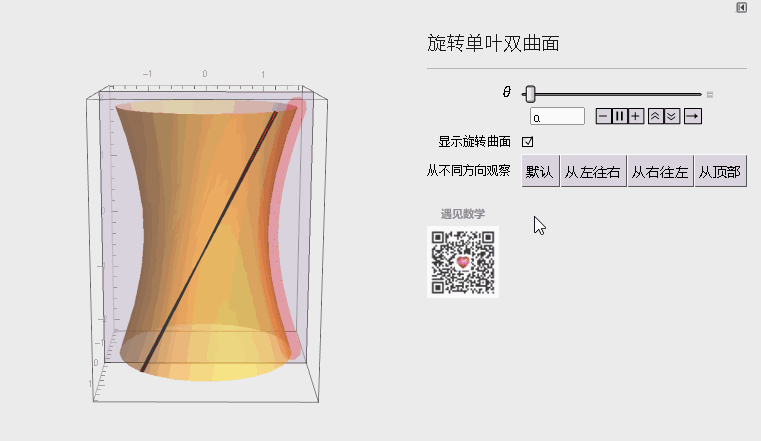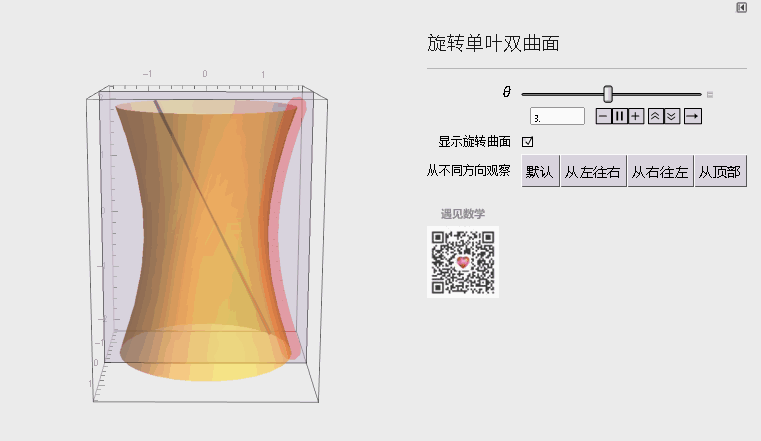
图5
这里也有一张机械旋转模型:

图6
四、维维安尼曲线
注意,这三个曲面方程平方项符号的区别。双叶双曲面系数符号是两负一正,图形特点就是对称,且图形分为两叶(部分),与坐标面平行的平面截得双曲线或椭圆
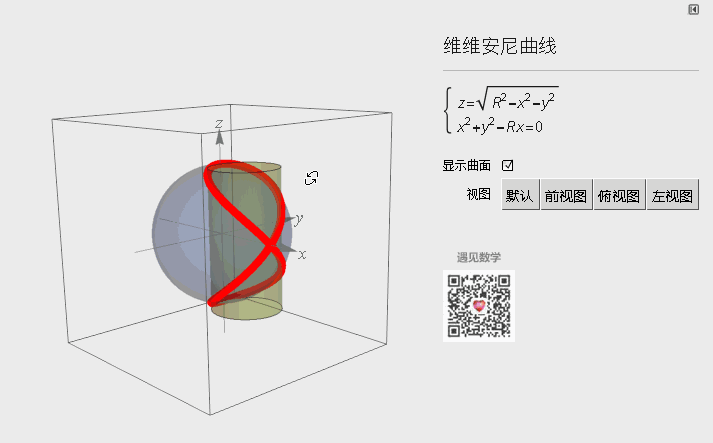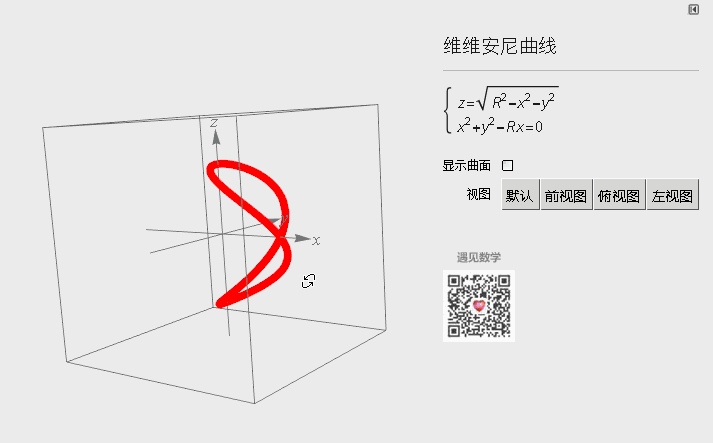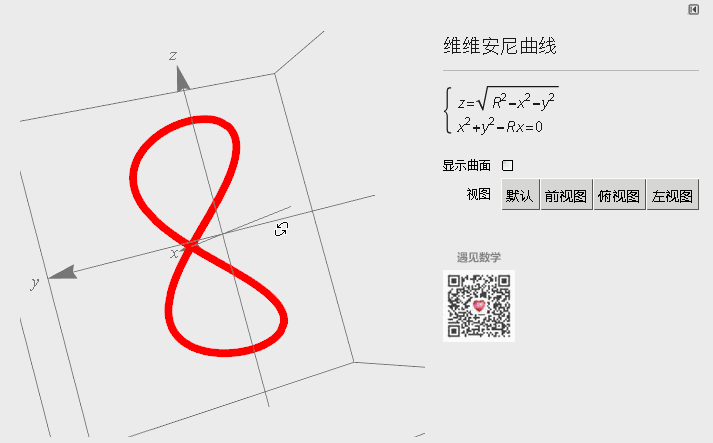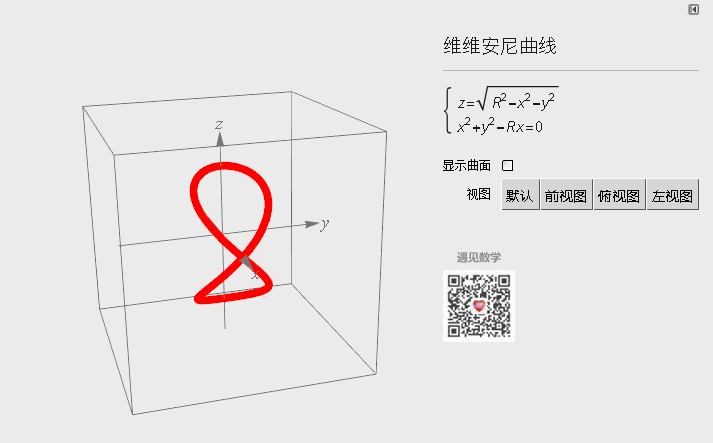
图7
以及相应的三视图:
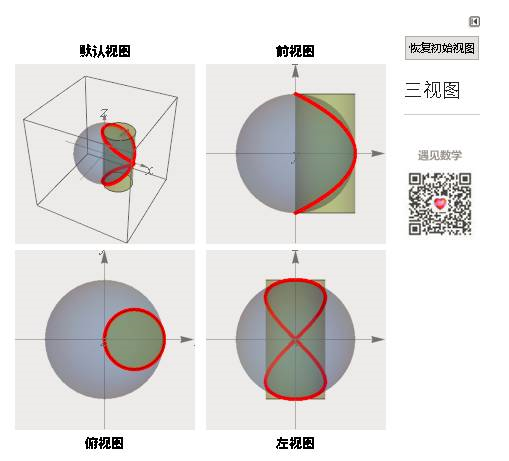
图8
上面就是利用Wolfram语言制作的图解高等数学例子。好了,现在让我们在下一篇的中来看一看高等数学相关的动图。
因为本人水平有限,疏忽错误在所难免,所以还请各位老师和朋友不吝赐教,多提宝贵意见,帮助我改进这个系列。感谢关注!Thanks!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











