用数学的方法来描述物体运动的轨迹(曲线),经常所用的方程除了平面直角方程,还有参数方程和极坐标方程。
参数方程是通过第三个变量去分别表示x,y,从而建立它们之间的关系的一种方程。某些曲线用参数方程表示比用其他两者方程表示更方便,简洁。
一、圆的参数方程
直接看图吧,我这里也将x和y的函数图像一并绘制出来了:

图1
二、直线的参数方程
如下直线参数方程表示通过点(a,b),且方向向量为(m,n)的直线:
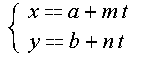
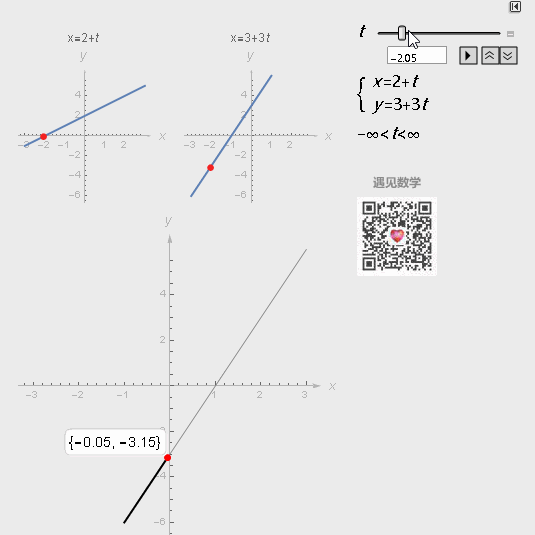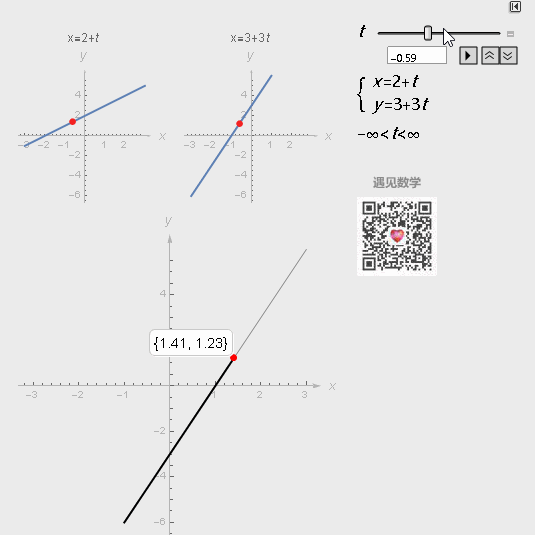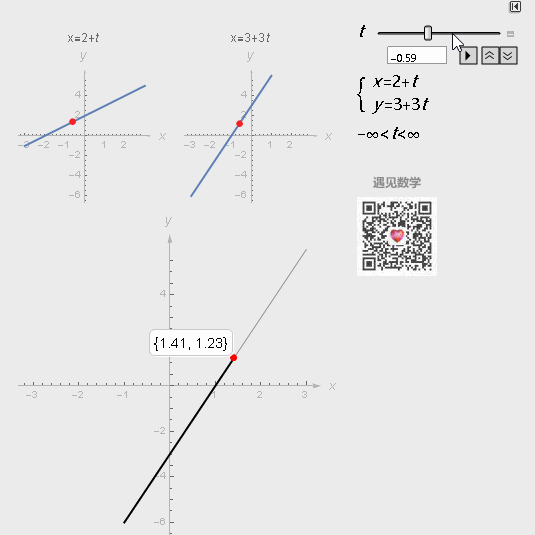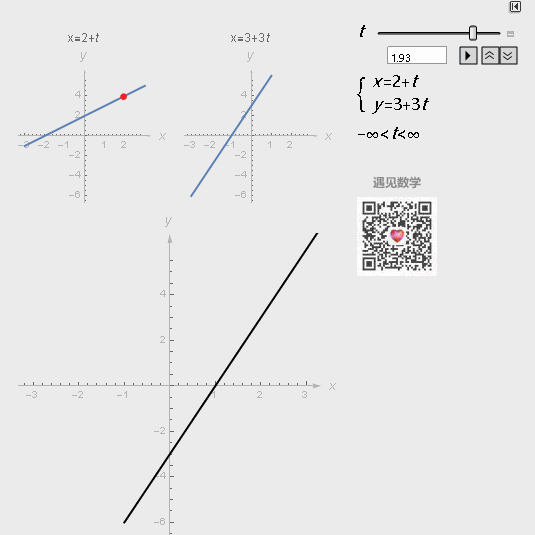
图2
三、摆线
摆线(Cycloid,又称圆滚线)。一个圆沿一条直线运动时,圆边界上一定点所形成的轨迹。
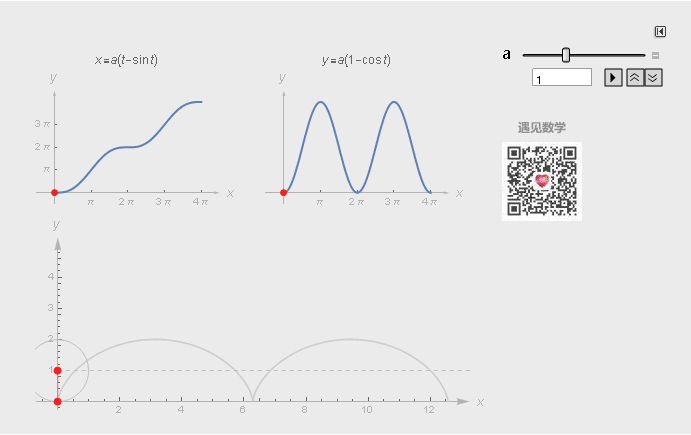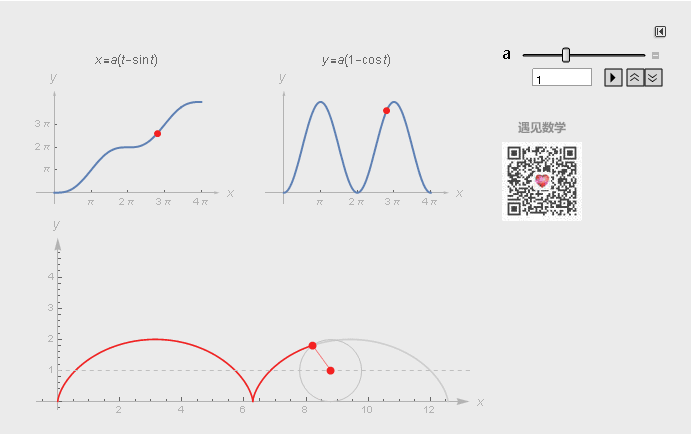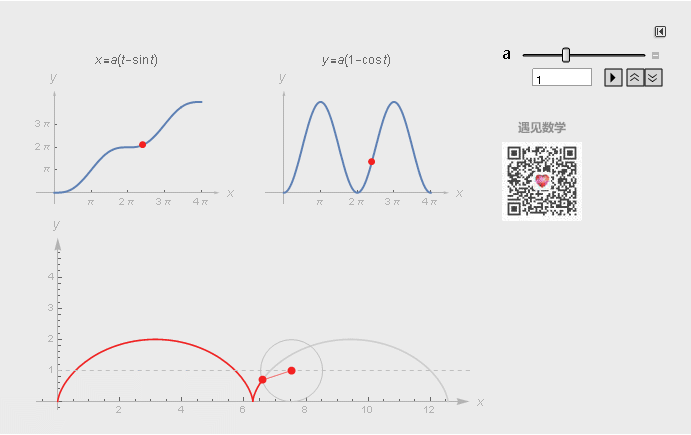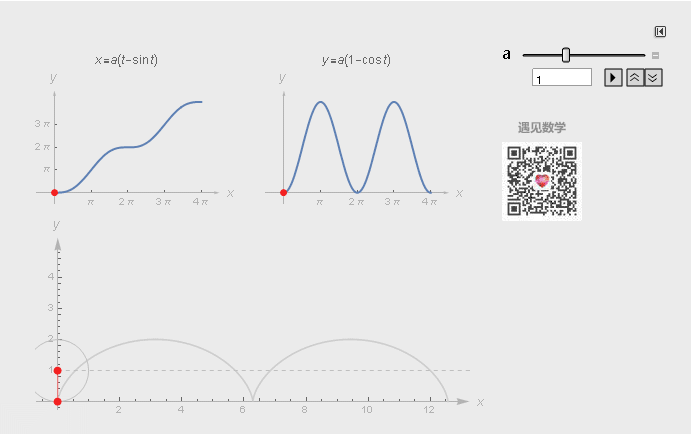
图3
有一个与摆线相关的问题就是最速下降问题。从A以速率为零开始,沿某条曲线,下降到B点,怎样的曲线能令所需的时间最短呢?最早由伯努利提出,也是由他本人来搞定滴。下面的动画很好的展示了最优就是一条摆线的结果:

图4
咱们回头在数学实验与建模中会再次碰到最速下降问题在Wolfram语言中是如何求解的。一些曲线同摆线紧密相关,如下面的内(外)摆线。
四、内(外)摆线
这里就看看内摆线(Hypocycloid,又称圆内螺线)参数方程表示形式:
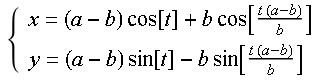
调整其中a,b参数,可以呈现出千变万化的图形出来:
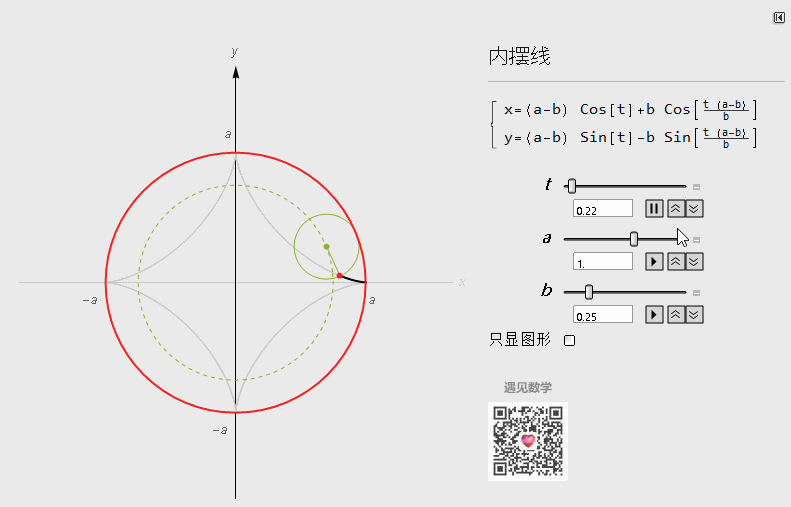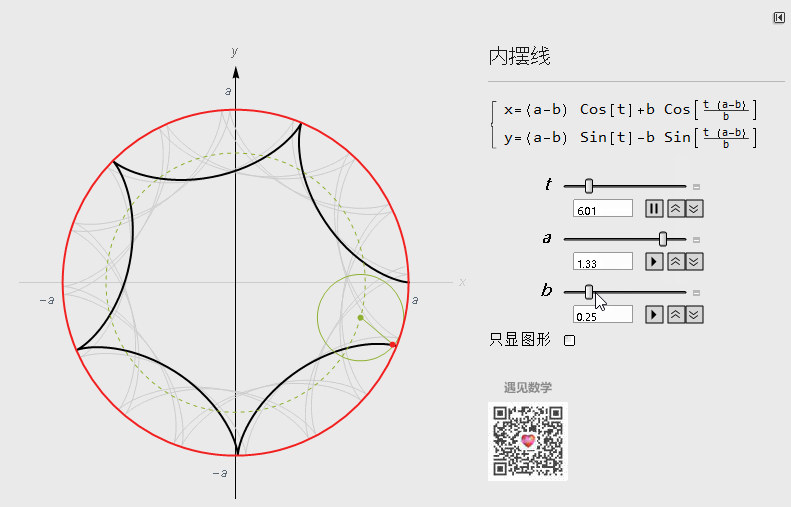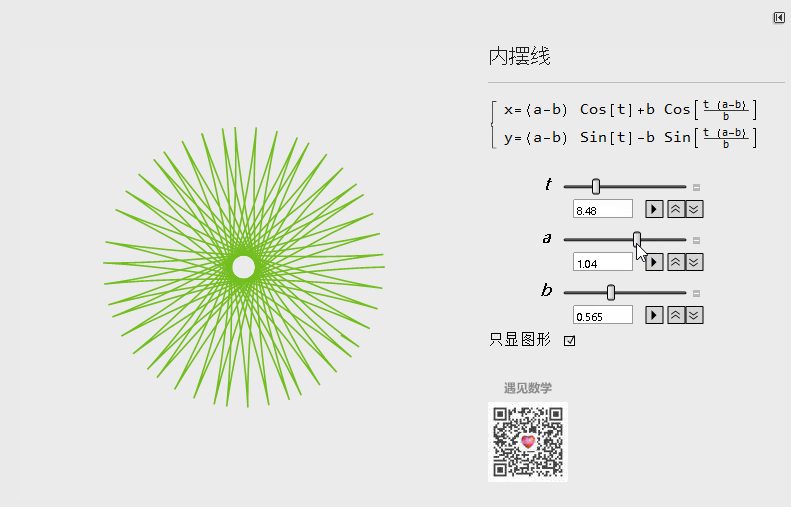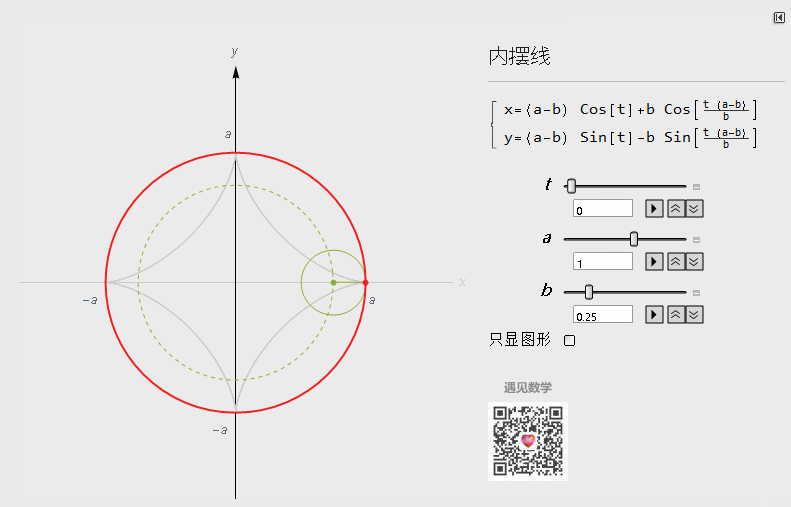
图5
当a=2b时候,轨迹为一条直线:
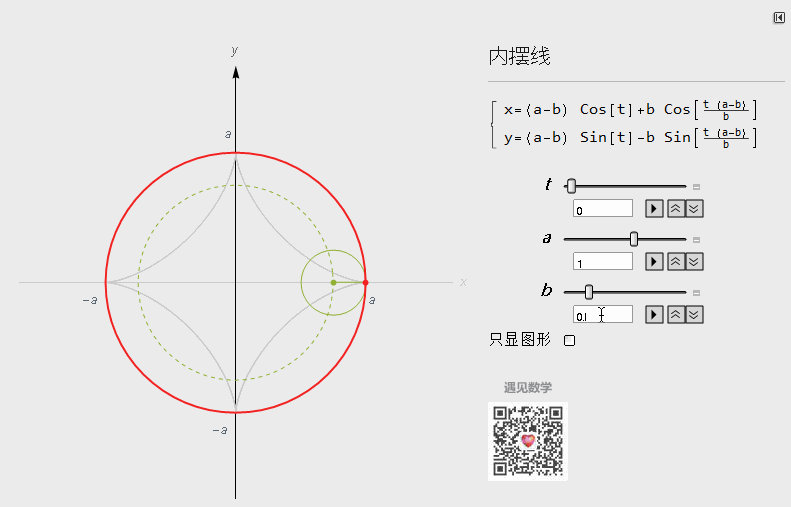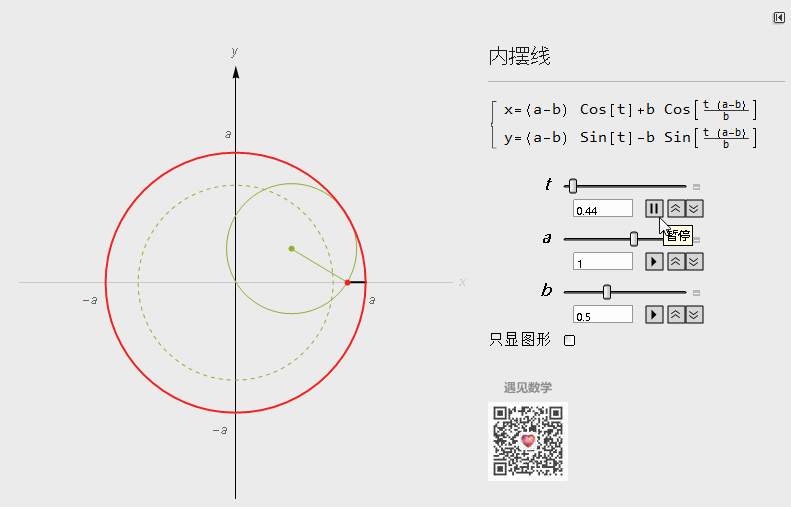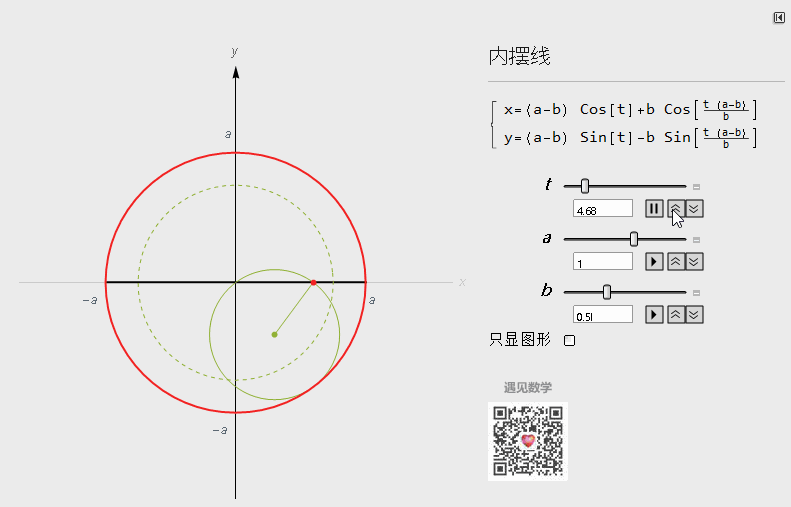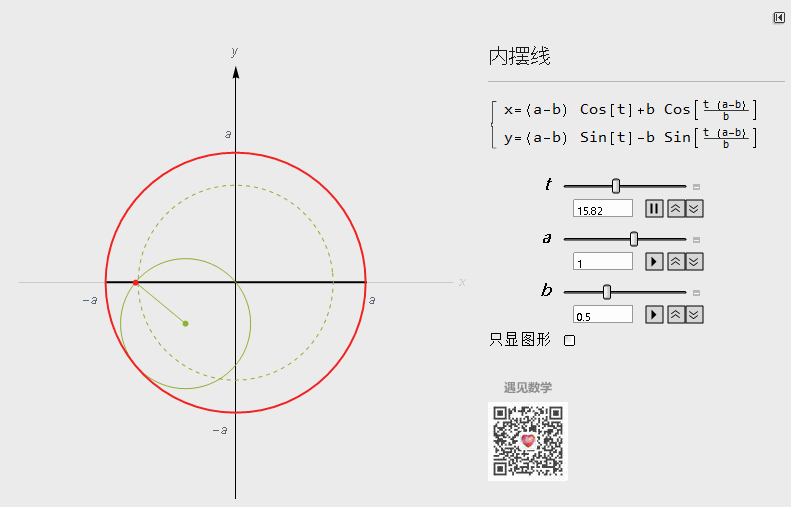
图6
外摆线(Epicycloid)这一版不再制作动画,可以用WolframAlpha查看相应公式及图画:

图7

图8
上面就是利用Wolfram语言制作的图解高等数学例子。好了,现在让我们在下一篇的中来看一看其他高数相关概念的动图。
因为本人水平有限,疏忽错误在所难免,所以还请各位老师和朋友不吝赐教,多提宝贵意见,帮助我改进这个系列。感谢关注!Thanks!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











