积分的本质就是计算某个区域上的总量,如果是一维区域,那就是在直线或者曲线(积分路径)上进行计算。
一、曲线积分(Line integral)
第一类曲线积分(对弧长的曲线积分)的物理意义就是求曲线质线的质量,f(x,y)为线密度,ds可以被看作积分路径上的一段很小的“弧长”。
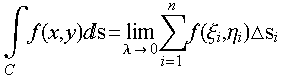
其几何意义上求柱面的面积:

图1
用等分点将C分成n小段,随着划分数量趋于无穷,小矩形宽度λ趋于0,而全部小矩形面积之和就等于柱面的面积:
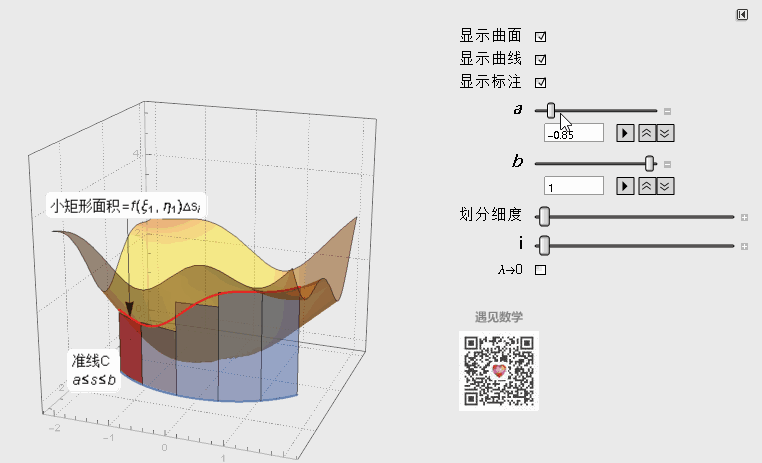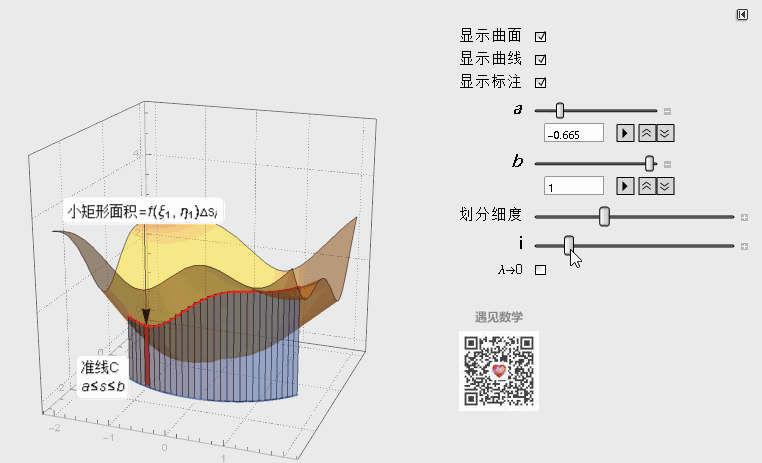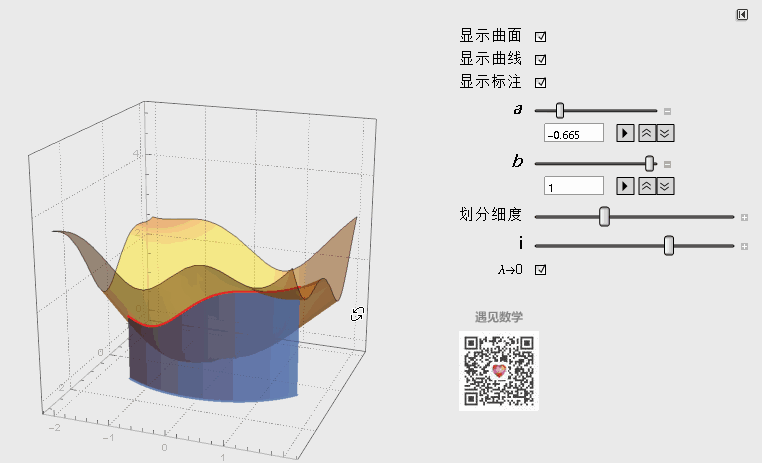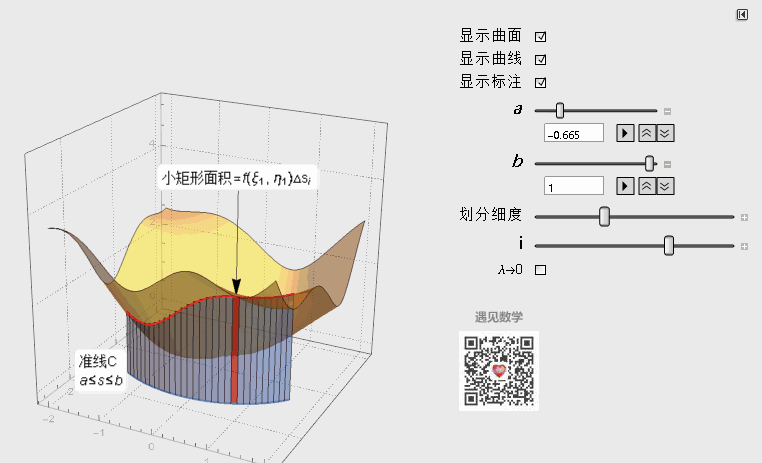
图2
第一类曲线积分的计算公式:
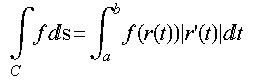
r(t)为相应的参数方程,并且r(a)和r(b)分别是路径曲线C的两个端点。具体计算的例子这里不再用可视化方式展示。
上面就是利用Wolfram语言制作的图解高等数学例子。好了,现在让我们在下一篇的中来看一看其他高数相关概念的动图。
因为本人水平有限,疏忽错误在所难免,所以还请各位老师和朋友不吝赐教,多提宝贵意见,帮助我改进这个系列。感谢关注!Thanks!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











