在介绍第一类曲面积分之前,有必要先再回顾看下投影的概念以及简单计算椭圆面积应用。
一、向量a在b方向的投影量
a在b方向的投影量长度k=|a|cosθ,当然如果要求的是投影向量就还需要乘以b的单位向量。
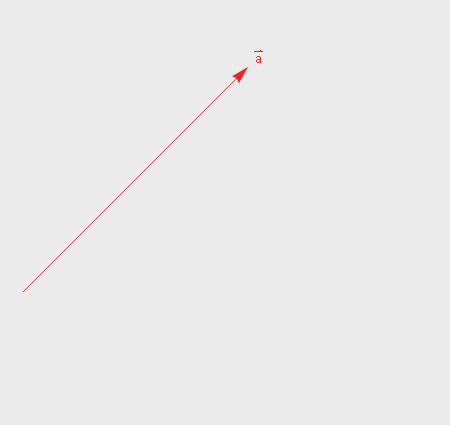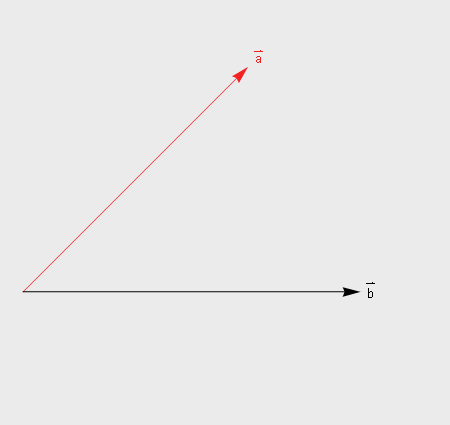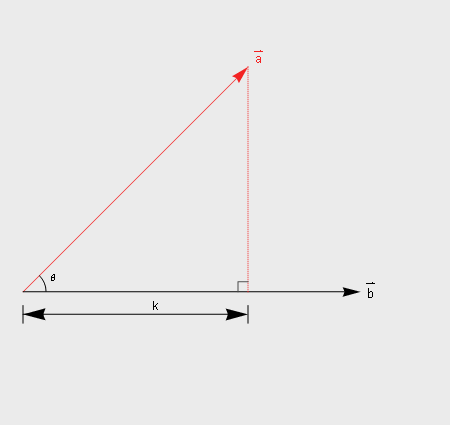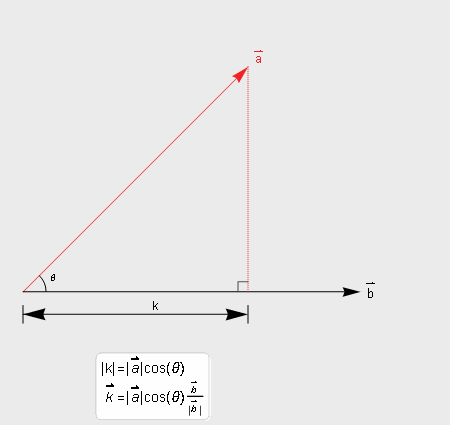
图1(注:有关向量的其他运算可以查看之前发布的图解高数相关内容)
二、面的投影
介绍完向量的投影,再来看面的投影。A在夹角θ方向上的投影面D。考虑D的面积肯定要比A要小,但是小多少呢?其实根据上面向量投影的思想就可以知道投影面积D=A cosθ。
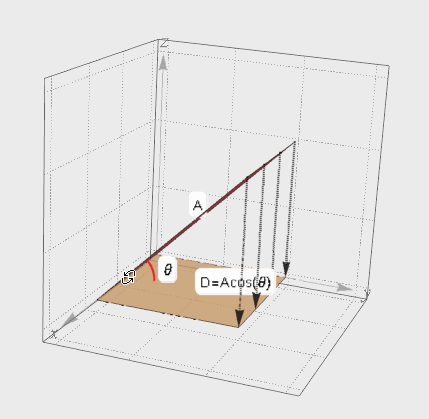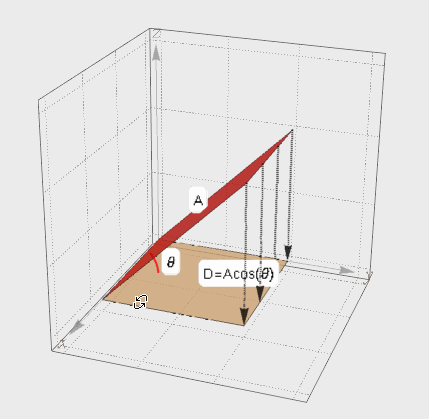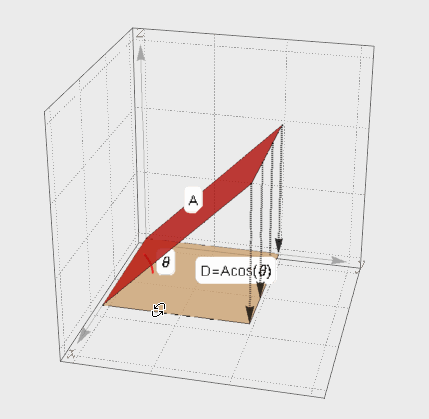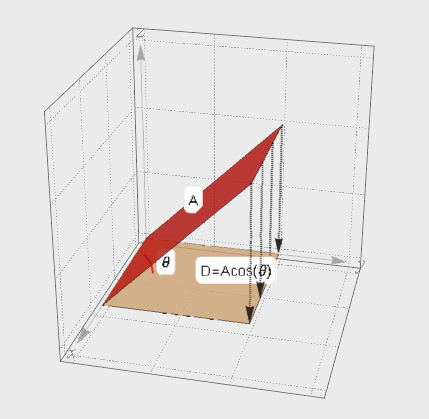
图2
三、投影的应用
那下面就看一个很简单的例子——求椭圆的面积,这里我们想象椭圆在三维空间中其实就是由一个圆的投影下来的形状,有了这个思路就可以用圆的面积乘以它们的余弦夹角,非常轻松就可以算出来了。
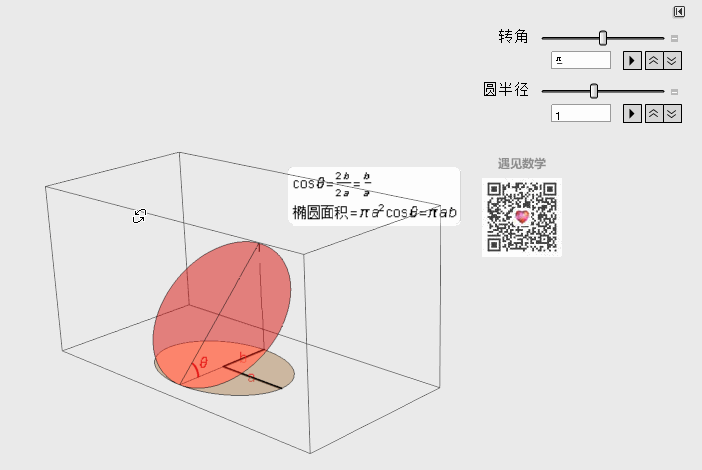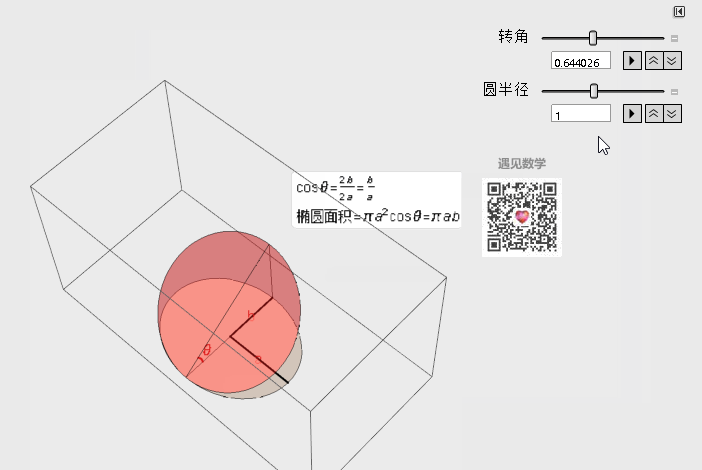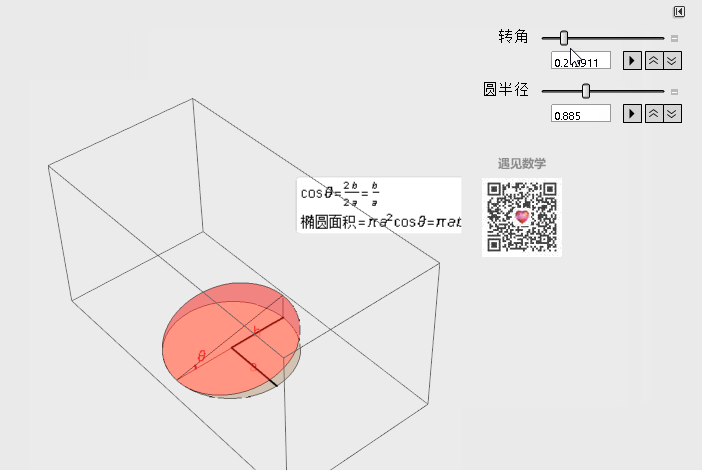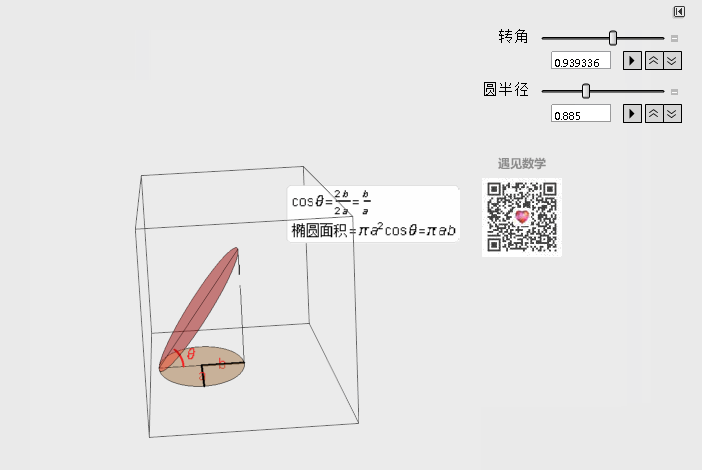
图3
上面就是利用Wolfram语言制作的图解高等数学例子。好了,现在让我们在下一篇的中来看一看其他高数相关概念的动图。
因为本人水平有限,疏忽错误在所难免,所以还请各位老师和朋友不吝赐教,多提宝贵意见,帮助我改进这个系列。感谢关注!Thanks!
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











