微信公众号【遇见数学】根据3Blue1Brown视频整理文字版,方便各位同学学习,还请多多转发支持我们继续前行。先来看下视频吧。
视频1

图1
在前几期视频中介绍了几个求导公式,有一个我没说,但还是非常重要的,就是指数函数。

图2
为什么我们可以说 ex 指数函数中是最重要的一个?首先,我们先来看看 2x,并假设自变量为时间t,比如说天数吧。函数值 2t 是人口数量。在t=0的时候,总质量就是 20=1,总的来说每天都翻一番。对于导数,我们要算的人口质量的变化率dM/dt,也就是人口数量的微小变化量除以时间的微小变化量。我们看看从第三天到第四天的情况:
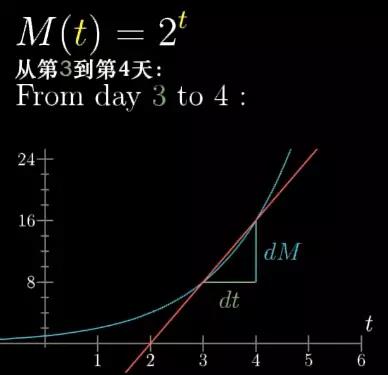
图3
在此情况下,人口数量从8涨到了16,也就是说一天增加了8个单位。注意这一增长率等于当天开始时候的人口数量。从第四天到第五天人口数量16涨到了32,增长率就是每天16个。这又等于当天开始时候的人口数量。所以总体来说每天的增长率就等于当天开始时候的人口数量。
你可能会猜想到 2t 的导数等于它本身,即此函数再给定时间t的变化率可能就等于函数值本身,这绝对是个正确的思路,但是还不完全对。
我们现在做的是在一整天之内做比较,就是考虑 2t+1 和 2t 之间的差别。但是要算倒数,我们要考虑变化量小之又小的情况。在1/10天,1/100天或者是10亿分之一天中增长又是怎样一种情况?
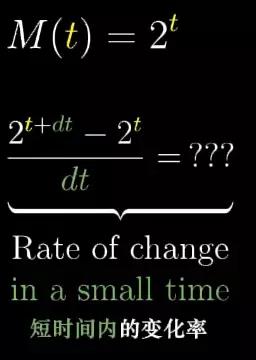
图4
更简单的来说,对一段极短的时间dt来说,我们要求的是在 2t+dt 和 2t 之间的差别,再除以时间dt,也就是单位时间内函数值的变化。
但现在我们研究的就是在给定时间点附近的一个极小领域,而不是以整天为研究单位。
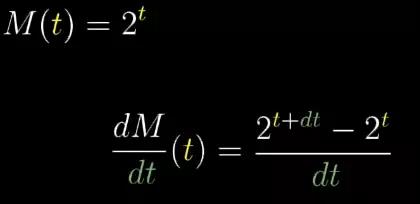
图5
指数函数的一项重要性质就是说,可以将其拆成 2t*2dt
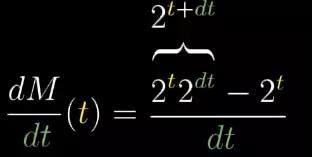
图6
这就能从加法的思想联系到乘法的思想上,比如变化率和比率。

图7
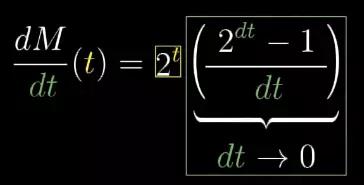
图8
嗯,别忘了 2t 的导数是在dt趋近于零的时候,上式所趋近的值。乍一看,貌似这一步并不重要,但是真正至关重要的是右边的这一项包含了所有dt的项。它和t的值本身彻底分开来,这一项就和我们开始的具体时间无关了。我们可以在dt这一项带有一个很小的值。

图9
这个数值就会不断的向一个特定的数靠近,大约是0.6931......重点是这是一个常数。不像其他函数的导数,所有和dt有关的项都和自变量t分离开来了。所以它的导数就是它自己本身,只不过乘以了的某个常数。

图10
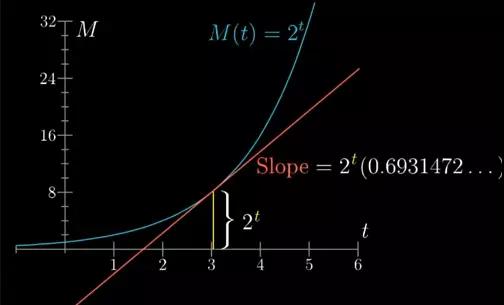
图11
这个性质并不是数字2独有的,如果我们给他换成函数 3t。指数函数的性质依然会使我们得出类似的结论,3t的导数和它自身成正比,只不过这回比例常数变成了1.0986。
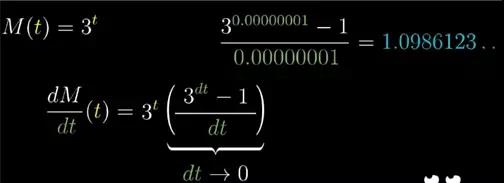
图12
对于指数函数的底数,可以换一换来看看对应的比例常数是多少。试试,看能不能找出什么规律来。

图13
比如当底数为8的时候正好是底数为2时候的比例系数的三倍,看来这些数绝不是随机的,一定有迹可循。但是什么规律呢?2跟0.6931有什么关系?8又跟2.079有什么关系呢?现在要提的第二个问题,它能够从根本上解释这些迷之常数。
这个问题就是有没有哪个底数,能够使这个系数为1。

图14
使得 at 的导数不仅仅和自己成比例,而是干脆等于它自己。有的,它就是特殊的常数e,大约等于 2.71828。
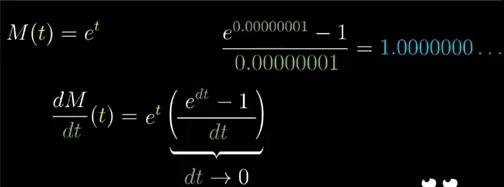
图15
所有的指数函数都和它们的导数成正比,但是只有单单一个e可以使得那个比例系数为1。也就它等于 et 就等于它自身的导数。
换一种看法,观察 et 的图像,它有这么一个特殊的性质,使图像上任意一点切线的斜率,都等于这一点到横轴的距离。

图16
有这样一个函数的存在,就解答了那个迷之常数的问题。现在我们就可以借助它来考虑那些和自己导数成正比函数了。关键就在于用链式法则,比如说 e3t 的导数怎么求?

图17
或者比起简单粗暴的代入公式,你可以借此机会,练习一下,上个视频中讲到的链式法则的直观理解。想想t的微小变化是如何影响3t的值,而这个中间值的变化又是怎样影响到了最终 e3t 的值。

图18
言归正传,关键就是 eConstantt 的导数就等于常数乘以函数本身,到了这一步,关于迷之常数的问题, 其实就变成了一个代数运算了,2可以写出eln(2),这一步只是利用了自然对数的性质。
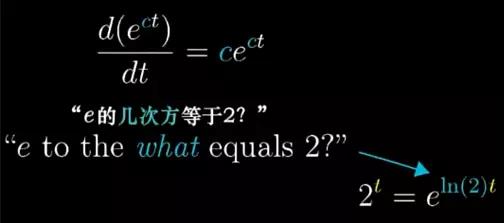
图19
因此,函数 2t 就等同于函数 eln(2)*t。结合我们前面所得的知识,et 等于它自身的导数,还有链式法则,而比例系数等于ln(2)。

图20
如果你计算ln(2)会发现,它就是0.6931,我们就就可以看到刚才的那个迷之常数。其他底数也是一个道理。我们求导时冒出的这个迷之比例系数,只不过就是底数的自然对数罢了,也就是“e的几次幂等于那个底数”这个问题的解。
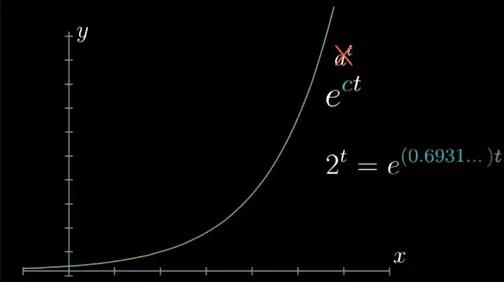
图21
事实上,纵观微积分的应用,你基本上见不到 at 这种形式的指数函数,指数函数基本上都是以 ect(c为常数)的形式出现的,并没有什么区别,任何 2t 或 3t 这样的东西都能写出e的常数乘t次幂。
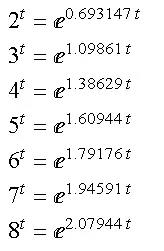
未来避免我们对符号太过关注,我想强调的是,写下某个特定的指数函数又很多很多方式。
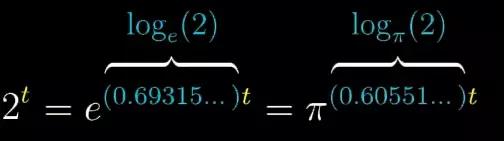
图22
你所见的写出e的某常数乘t次幂的表达方式,只不过是我们选择的一种写法罢了,e并不是这个函数的根基所在,但是将指数函数写出含有e的形式好处是,对指数上这个常数就有了一目了然的。

图23
我们来看个例子,在许多自然现象里,变化率都和变化量成正比,在不考虑资源有限会导致增长放缓的话,这一比率往往就和数量成正比。
此外,在凉爽的房间内放一杯热水,水变凉的速率就和水与房间的温差成正比。或者换个说法,温差的变化率就和温差本身成正比。
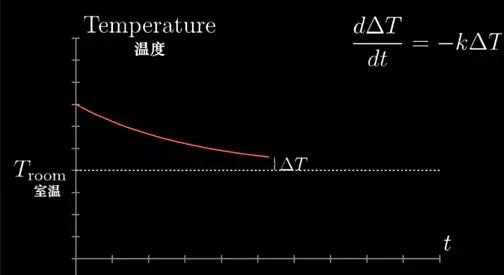
图24
再假设你做投资,那么金额的增长率就和任意时间点的金额成正比,在以上所有例子中,变化率都和数量本身成正比。
在以上所有例子中,变化率都和数量本身成正比。因此该数量随时间的变化,看起来就会像指数函数,尽管指数函数又很多种写法,但是选择将表达为 ect(c为常数)是非常自然的,因为那个常数有着非常自然的含义,它就是变化率和数量本身这两者的比例系数。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











