微信公众号【遇见数学】根据3Blue1Brown视频整理文字版,方便各位同学学习,还请多多转发支持我们继续前行。先来看下视频吧。
视频1

图1
我想说件我初学微积分时感到特别奇怪的事情,我们从以xy直角坐标系的原点为圆心,作一个半径为5的圆。这个圆可以用等式 x2+y2=25 来定义,记这个圆上所有的点离原点的距离都是5。按照勾股定理的下面图中等式。
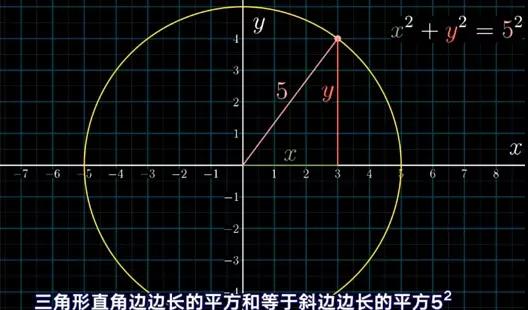
图2
现在讲求圆上一点切线的斜率,比如经过(x,y)=(3,4)这点的切线斜率。当然经过该点的切线一定会垂直于经过该点的半径。但是假设你还不知道这一点,或者是你想学习一个求任意曲线切线斜率的通用方法。
对于求曲线的切线斜率,我们可以从这里突破。我们把曲线不断放大,直至它和切线能几乎重合,然后想象沿着曲线迈出微小的一步(增量)。我们把这一小步在y轴的变化叫做dy,在x轴的变化叫做dx。那么所求切线的斜率就是沿曲线上升除以前进得来的dy/dx。
但不同于之前所有微积分中的切线斜率问题,这里我们的曲线并不是一个函数图像。所以我们不能单纯地对它求导。因为它不存在什么取值的微小变化所造成函数值的微小变化这样的说法。因为不存在一个x对应一个y这样的映射。
x和y是同时有一个等式定义,而相互联系在一起的。这种曲线就是所谓的隐函数曲线(implicit curve)。即满足某种关于变量x和y的性质,所有(x,y)点的集合。
还是学生的时候,我就对这种曲线上的dy/dx的过程感到十分困惑。我们要对表达式的两边同时求导:
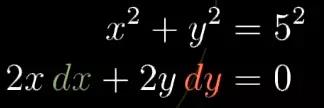
图3
你是不是也会感到困惑?对这种带多个变量的表达式求导,究竟是什么意思?我们为什么要处理如此微小变化量的dy和dx。不过如果你继续将上式进行转化的话,最终你就可以变换得到dy/dx的表达式。这里,它就是dy/dx=−x/y。
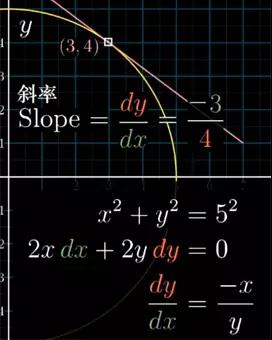
图4
那么经过圆上(3,4)点的切线斜率就是−3/4。这个奇怪的过程叫做隐函数求导/隐微分(implicit differentiation) 。
下面我来看看对两个变量的表达式求导的问题先放一放,我先讨论另一个紧密相关的问题——相关变化率问题(Related Rates Problem)。
假设我们有一把五米长的梯子斜靠在墙上,梯子顶端离地4米,那么由勾股定理可得,此时梯子的底端距离墙角3米。现在梯子的顶端开始以1米每秒的速度下滑。问题是,在这一开始的瞬间,梯子底端离开墙角的速度是多少?
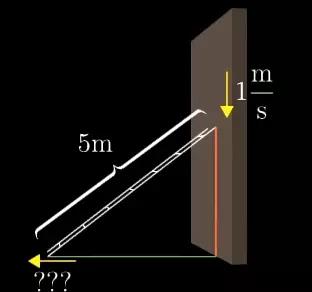
图5
问题很有意思吧。梯子底端离墙角的距离其实是由梯子顶端的离地高度所决定的。那么我们此时可以算出两头移动速度的关系。但是这个关系具体如何,我们并不清楚。
首先给这些变量命名,那么梯子顶端离地的距离标记为函数y(t),毕竟梯子在运动,这个距离由时间决定,同理,底部离墙的距离我们就标记为函数x(t)。两个函数可由一个等式联系起来 x(t)2+y(t)2=52 。
这个等式之所以关键就在于它时时刻刻都成立。要算底部的移动速度,一种办法是把x(t)单独表达出来。用1米/每秒的滑落速度算出y(t)大概长什么样,在对这个函数求导即可。dx/dt就表示x根据时间的变化率。
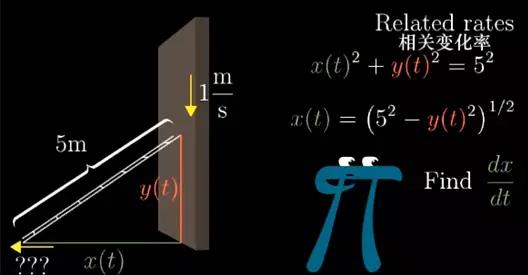
图6
这么做没什么问题,用几层链式法则就可以算出来的。但是我想给你演示一种从不同角度来解决问题的办法。
等式的左边是一个关于时间的函数,那刚好就等于一个常数,也就是说它的值是不随时间而改变的。但我们依然把它写成了一个关于时间的式子。这就表示我们能把它当做关于t的函数对待。

图7
其实我们对等式左边求导,就其实是在问:“经过一小段时间dt,y会减少一点点,而x会增加一点点,那么整个表达式的值会变化多少?”。
一方面,很显然表达式导数就是0,因为它等于常数。常数是不随时间变化的,保持恒定的数;另一方面,你对等式左边求导会变成什么样?
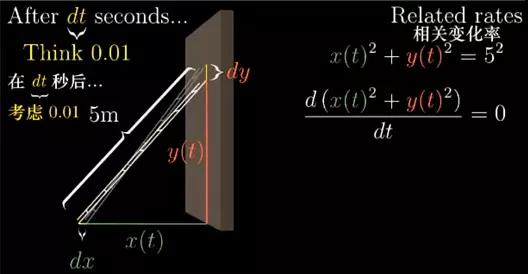
图8
x(t)2 的导数就变成了2*x(t)*(x的导数),这就用到了上一集提到的链式法则。2x*dx就表示因为x的变化而导致的 x2 的变化量,然后再除以dt;同理y(t)2 的变化率是2*y(t)*(y的导数),最后,这个表达式必须等于0。其实这就等同于要求 x2+y2 的值不随梯子滑动而改变。

图9
在运动开始时,t=0,离地高度y(t)=4 m,离墙距离x(t)=3 m。又因为梯子开始以每秒1米的速度滑落,就表示导数dy/dt=−1m/s,将其代入上式,现在dx/dt就能算出来了。
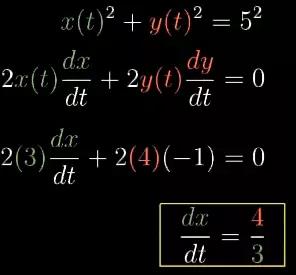
图10
我用这个梯子的问题是想要大家比较它和求圆切线直接的关系。两个问题中,我们都有一个等式 x2+y2=52 。解决两个问题,我们都要对等式两边同时求导。
但梯子问题中,表达式是关于时间的函数,那么我们求导是有明确的意义的,我们想要求表达式随时间的变化率。
但圆切线问题奇怪的一点就在于我们不用一个微小的时间变化dt去联系其导致的x和y的变化。导数里的微小变化量dx和dy看上去像是凭空冒出来的,并不靠一个共同的时间变量来联系。
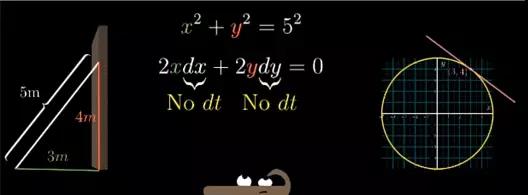
图11
这里教大家一招,给表达式 x2+y2 取个名字S,S实际上就是取两个变量的函数,对于平面每一点(x,y),它都会返回一个值。对于这个圆上的所有点来讲,这个值就是25。
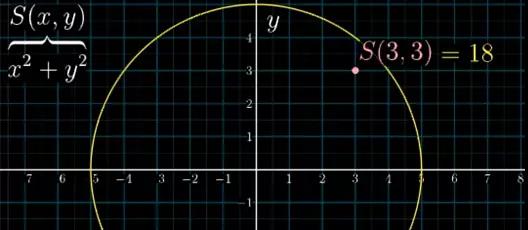
图12
点往圆外走,这个值就越大,而点(x,y)向圆心走,这个值就越小。
那么给这个表达式S求导的关键是要考虑S的两个变量同时发生了变化,既有x的微小变化量dx,也有y的微小变化量dy。
此时,我们不管这个变化还会不会留在圆上,我们就在xy平面上往任意方向走了微小的一步。给S求导就是再问“走了这一步, S 的值变化了多少”。由这一步而导致S产生的变化,就是我这里写的dS。
举例来说,我们从坐标x=3, y=4这点开始移动,移动的变化量dx =-0.02, dy =-0.01。
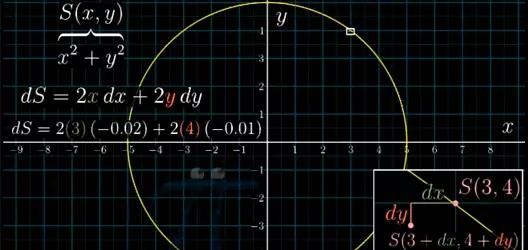
图13
那么S减少的值,即 x2+y2 随这次移动变化的量,就是差不多2*3*(-0.02)+2*4*(-0.01),这才是导数表达式2x*dx+2y*dy的真正含义。
它实际是表示你从(x,y)点开始,走了(dx, dy)这一小段距离之后,x2+y2 的值相应变化了多少,对于所有的求导而言,这只不过是近似值,但是这个近似值会随着dx和dy越来越小而越来越精确。
重点在于,当你把这每一小步都落在这个圆上的时候,你等于就是需要S的值维持不变。
S开始是25,你要让S一直保持25 ,那么这样dS就应该是0。那么我们要保证每一步都踩在圆上,条件就是要让表达式2xdx+2ydy一直等于0。
严格意义上讲,这个条件实际是保证每一步都落在过圆的一条切线上,而不是圆本身。
但如果步子足够小的话,也就没区别了。当然我们选择分析 x2+y2=52 没什么特别的理由,我们再来看另一个表达式sin(x)*y2=x,用图像表示出来就是一些U型曲线,当然这些曲线其实就是一群(x,y)坐标点的集合——满足sin(x)*y2正好等于x所有点的集合。
现在我们想象从曲线上移动了一小段距离(dx, dy),暂不考虑落脚点是否还在曲线上。对表达式一边求导,就可以算出这一小步使得等式这一边的值变化了多少。对等式左边求导,我们得使用乘积法则。
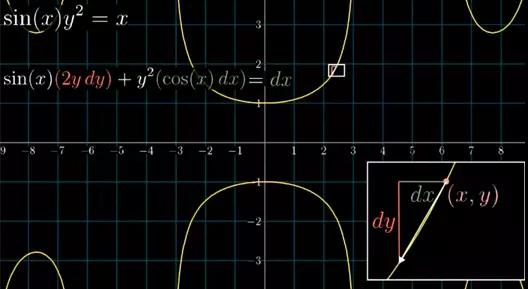
图14
让这取导后的两边依旧相等,其实就是在说:“无论你这一小步 (dx, dy)移动了多少,只有当左边的变化量等于右边的变化量时,这一步才能依然落在曲线上”。只有这样,上面的这个等式才能依旧成立。从这样出发,根据解题的需求,就可以用代数解决剩下来的问题了——算出dy/dx。
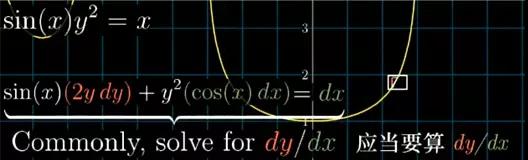
图15
在最后一个例子中,我要演示可以利用隐函数求导的方法,从已有的导函数,推算出别的函数的导函数。
之前提到过 ex 的导函数就是它本身,那么它的反函数x的自然对数ln(x)的导函数又是怎样呢?
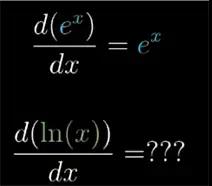
图16
ln(x)的图像,我们可以想象成一个隐函数的曲线,即xy平面上满足等式y=ln(x)所有点的集合,只不过这回等式中的x和y并不像之前例子中的那么错综复杂。
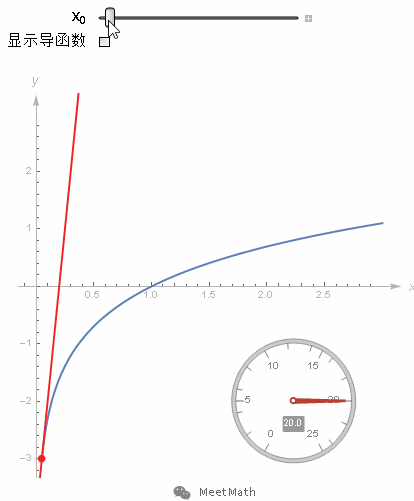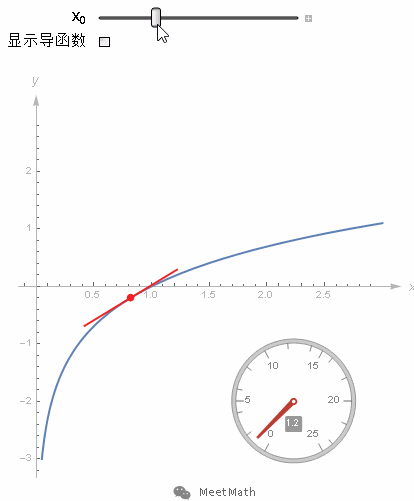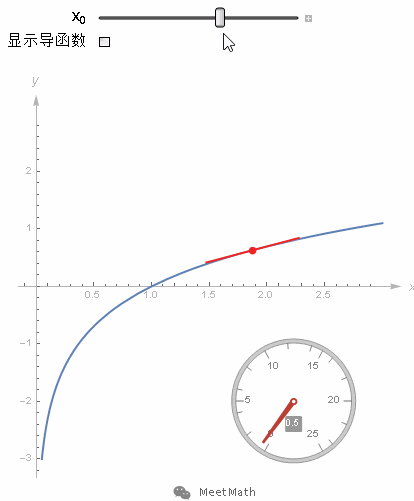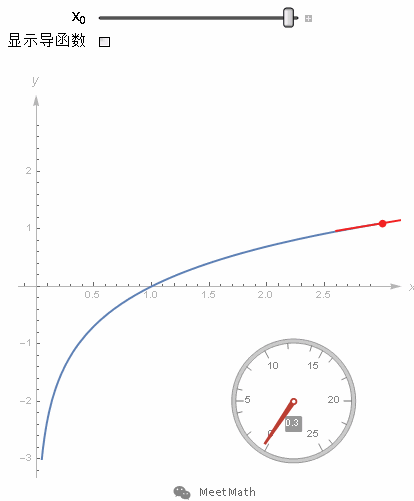
图17
这个图像的切线斜率dy/dx就应该是ln(x)的导函数。那好,首先把函数y=ln(x)变形为 ey=x,对两边同时求导,也就是考虑从图像上移动微小的一步(dx, dy)对等式两边各有什么影响。要让这一步依然落在曲线上,那么等式左边的变化量 ey*dy 就必须等于等式右边的变化量dx。
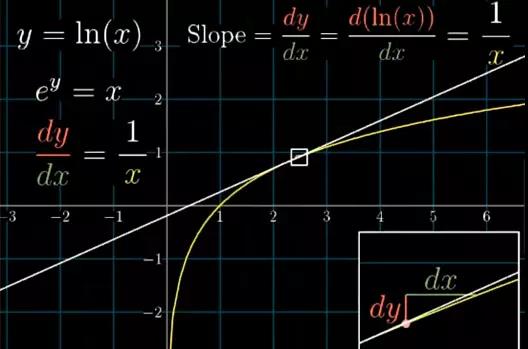
图18
对其变形,可得图像的切线斜率dy/dx等于 e-y,根据题目定义,对于该曲线上的所有点 ey=x都成立。由此可得斜率就是1/x。
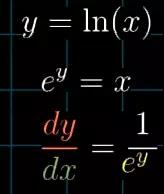
图19
现在图像的切线斜率,即图像的导函数就可以用关于x的式子表达。最终得出ln(x)的导函数是1/x。
顺便提一下,这集所有的内容其实都带你进入了一点多元微积分(Multivariable calculus)的门。多元微积分就是分析多个变量的函数,分析它们如何随多个取值的变化而变化。但要点总是一样的,你必须在大脑里想清楚,这些变量是如何联系在一起,如何变化的。
下一节的主题是极限,来看如何用极限的思想去理解导数。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











