微信公众号【遇见数学】根据3Blue1Brown视频整理文字版,方便各位同学学习,还请多多转发支持我们继续前行。先来看下视频吧。
视频1

图1
最近几期视频一直在讲如何求导,在我们开始讲积分之前,我想先花点时间讲下极限。极限的概念不是什么新事物,如果你们知道“逼近”的概念,你们大概也已经知道了极限的定义——就是一个数值逼近另一个数值。

图2
不过有这么几个理由,使得为此有必要做这一期的视频。

图3
第一,我得解释到目前为止我所描述的导数是如何跟教科书上严格的定义联系在一起的。我想让你们有底气把df,dx考虑成具体存在的非零变化量,并非仅仅利用直觉,而是一整套由严谨的导数定义所支持的。
第二,我也会借助极限的ϵ−δ定义来解释下数学家口中所说的“逼近”是什么意思。
最后,我们会用神奇的一招洛必达法则来计算极限。
首先,让我们看看导数的正式定义,函数f(x),求函数在某点,比如x=2点处的导数。主要观察x的微小变化量dx和其对应函数值的变化df。
这个比值df/dx若把它看做介于图像变化的起点和终点之间一条割线,那它离导数就差那么一点点。当dx逼近0时,这个比值逼近的才是真正的导数。
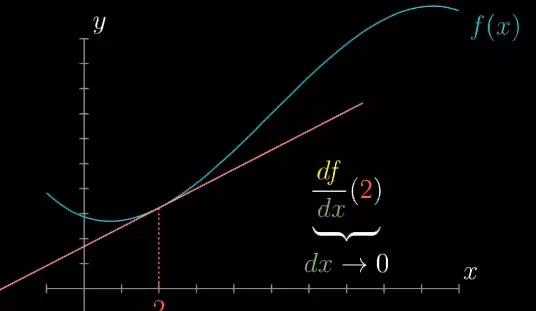
图4
说的再详细点,自变量对df的影响,就是下式:

图5
为了表示出你想求的是,当dx逼近0时的这个比值,你在左边写上lim代表极限,底下写上“dx→0”。
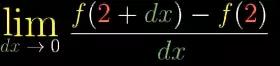
图6
你几乎不会在极限表达式里面看到带小写字母的d的项,比如dx。事实上,极限的标准形式会使用另一个变量,比如△x或h。
我个人认为原因是导数中带有d的项,已经包含了求极限的概念。把dx当做逼近与0的一个量。
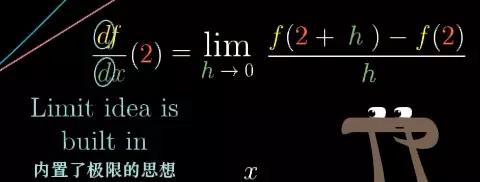
图7
在某种意义上说,这式子左边的df/dx就是等号右边这个式子的缩略版。只不过右边式子解释了df的含义,并且明确地写出了求极限的过程。而且是导数的标准正式定义。

图8
并且请注意右边式子里已经根本不存在无穷小悖论,这里的h跟我们一直在用的dx是完全一回事。dx被用来表示函数f取值的有限小的变化量,比如0.001等。同样,对于h也是一回事。
人们之所以在定义极限时引进新的变量h ,是因为这样就能明确取值变化量h是一个普通的数,和无穷小没有半毛钱的关系。因为有人喜欢将dx解释为无穷小的变化量。但其实你应当将dx解读为一个具体的,有限小的变化量,并记住随时考虑dx逼近于零的情况。
因为这样可以帮助你们更直观的理解微积分的法则是怎样来的。用具体的有现象的变化量来描述导数,其实和导数的正式定义是等价的。
我们讨论极限时,讨论的是当变量逼近于零时候的影响,而非无穷小变化量的影响。
下面看看本节课的第二个目标,正确地理解一个变量逼近定义一个变量的含义。

图9
考虑 ((2+h)3−23)/h,也就是函数 x3 在 x=2 这个点处导数的表达式,不过我们先把它看作一个变量就是h的函数。
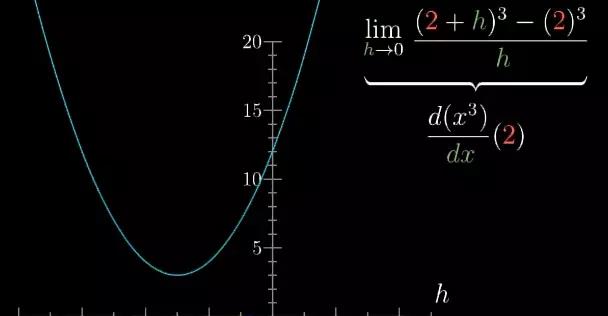
图10
它的图像就是一条连续的抛物线,这也说得通,因为这个函数就是3次项除以一个1次项。但实际上如果你看看h=0的地方。那个函数应该在0处有间断点。一般情况下,你需要用一个中空的圆圈来突出这个间断点。但请记住,当无限接近零的时候,函数依然有定义。
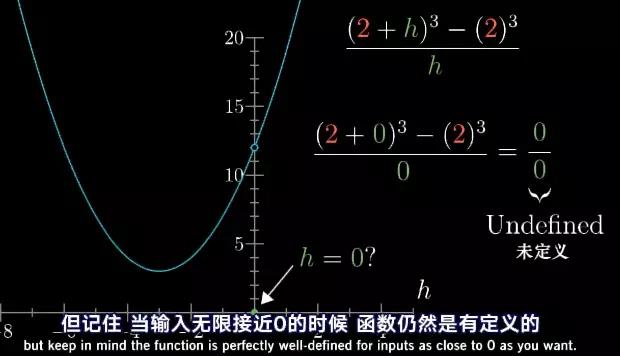
图11
当h逼近0的时候,函数的值,系这条虚线的高度是逼近于12。而且这个结果,从函数哪一边逼近无关。当h趋近于0的时候,这个比值的极限是12。
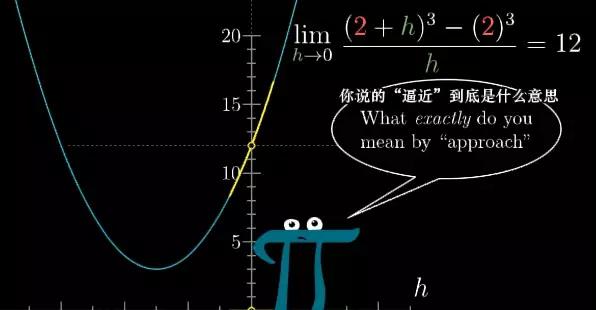
图12
但假设你是个发明微积分的数学家,有个孩子问你:“逼近到底是什么意思?”。尽管我们知道它的意思是一个值离另一个值越来越近。但数学上更清晰的解释是下面这样。
对应x=0附近的一些取值,除去禁忌的奇点x=0处,我们来观察这些点对应的函数值。也就是函数在这些点的高度范围。
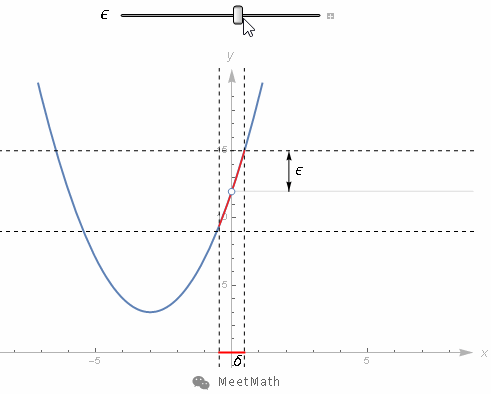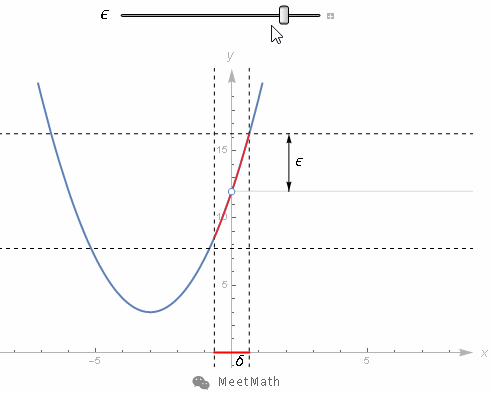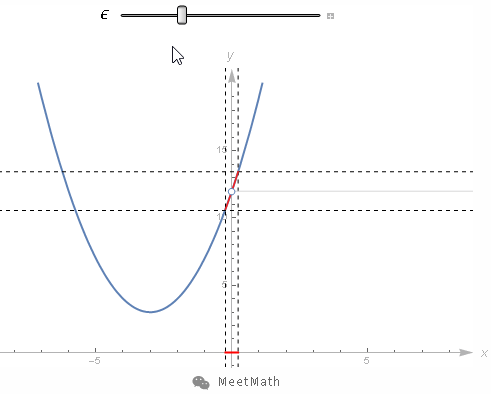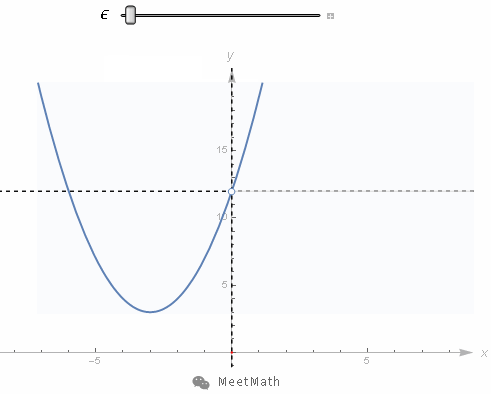
图13
当取值的范围在0附近不断缩小,可以看到函数值的范围越来越接近12。并且更重要的是你可以让这个范围任意缩小。
举个反例,现在看下面函数在0点也没有定义,但在0处函数跳跃了一下。所以当从右边逼近h=0这个点时,函数值逼近与2。当从左边逼近于0,函数值逼近1。因为当h逼近于0时候,函数值不确定。所以在这个点极限不存在。
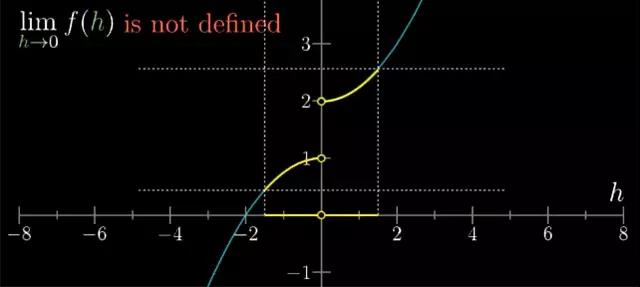
图14
也就是说当你盯着零点附近的取值和对应的函数值时。当你将取得的范围缩小时,函数值不会收缩到某个特定值上。
这种将取值范围再极值点附近收缩,然后观察函数值是否收缩,以及收缩后范围的方法,就是所谓的极限的“ϵ−δ”定义。
你可能认为这既繁琐又没有意义。但从这我们可一瞥实分析的冰山一角,也会让你们体验数学家如何把直觉中的微积分的理念完善细致的。
你们已经看到中心思想了,当极限存在时,你可以让函数值的范围任意缩小;当极限不存在时,无论你怎么将函数取值范围收缩,都无法将函数值范围缩小至某一确定值上。
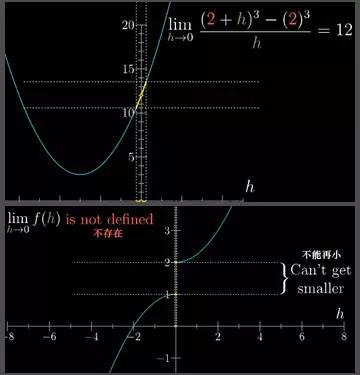
图15
在这个例子(下图)中极限值是12,考虑到任意函数值到12的距离,习惯上会用希腊字母ϵ来代表这段距离,而且这段距离想要多小随你来定。
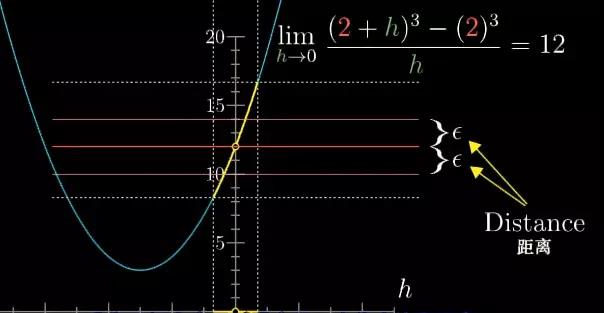
图16
极限存在的前提就是,你总能在极限点附近,离0点距离为δ的取值范围内找到一系列取值点。使得范围内的任一取值点它的函数值都处在距离12±ϵ的范围之内。
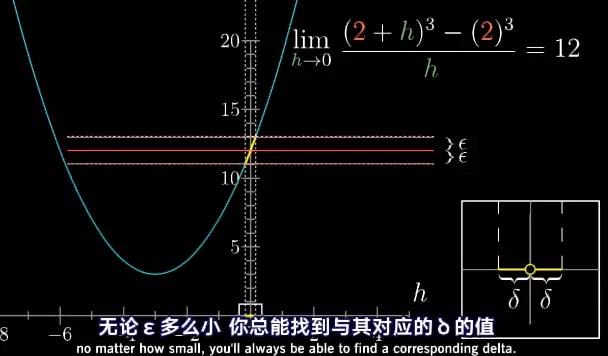
图17
关键是,这种情况对任意ϵ都成立。无论ϵ多么小,你总能找到与其对应的δ的值。
当极限不存在时,比如下面图的例子,你可以找到足够小的ϵ,比如0.4,无论你怎样缩小在0点的附近的范围,无论δ多小,其对应的函数值范围都会太大,找不到任何可以逼近的极限值。
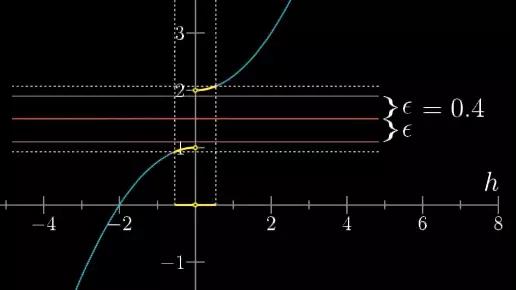
图18
上面这些都太理论化了,极限用来定义导数,ϵ和δ被用来定义极限本身。让我们用一个计算极限的技巧来结束吧。

图19
举个例子来说,假设你正在研究函数sin(πx)/(x2−1)——某种阻尼振荡的模型。当你取很多点描绘起来时,似乎是连续的图形。不过当x=1(或-1)时,会发现分子分母都等于0 ,所以函数在这点没有定义,图像上应该有个间断点,看起来应该在这个点逼近某一个确定的值。
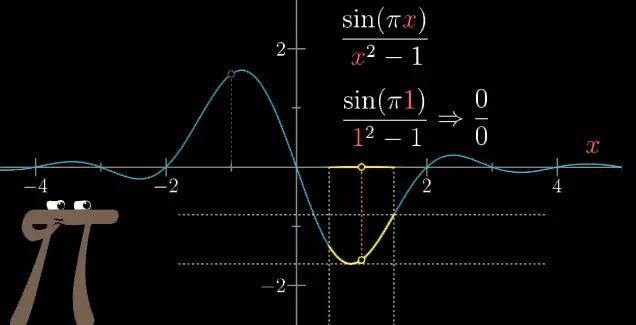
图20
你可能会问,既然你没有办法直接代入x=1,那你怎么知道相应函数值的结果呢?一种估算的方法就是取很靠近1的值,比如说1.00001。
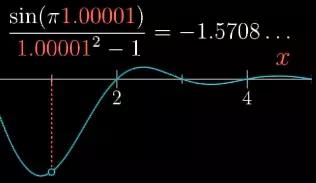
图21
有没有哪个办法能计算,这样0/0型的极限呢?
当极限帮助我们确定了导数的定义之后,导数还可以报答呢,帮助我们求解极限。
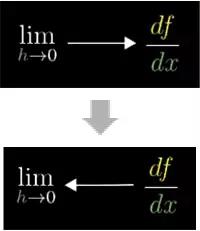
图22
让我详细解释一下,这是sin(πx)的图像,这是x2−1的图像,在x=1这个点上,两个函数的值都为0,都穿过x轴。我们可以效仿之前在x=1附近取一个特定的值,比如1.00001的做法。对图像放大,考虑某个微小的变化量dx对其的影响。
sin(πx)会减小,变化量dx对函数造成的影响就是这个函数值的变化量——d(sin(π x))。我们对导师的了解可知,应用链式法则,这个值应该是cos(πx)*π*dx。将x=1带入这个表达式中
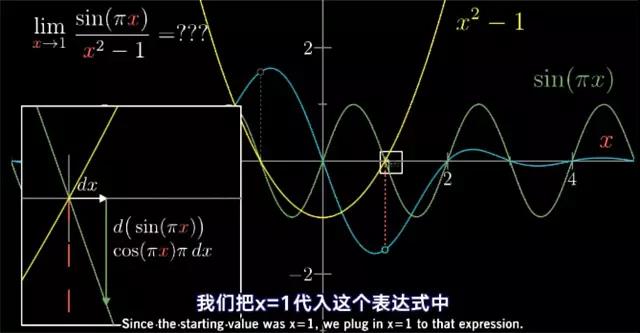
图23
换句话说,图像sin(πx) 的变化量与dx应该是成比例的,这个比例为常数cos(π)*π。由于cos(π)=-1,所以这个表达式可以写成-π*dx。
同样,x2−1图像变化量为d(x2−1)。求导之后,这个变化量应该为2x*dx。同样代入,x=1。这个变化量就是2*1*dx。
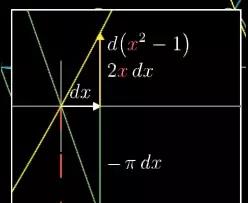
图24
所以对于点x=1距离为dx点来说,sin(πx)/( x2−1)的值大约就是−πdx/2dx,上下的dx相互抵消后,这个比值就是−π/2。
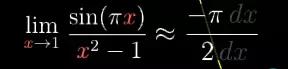
图25
对于之前的分式来说,dx取的越小,这些变化量就越精确,所以−π/2这个比值告诉了我们,当x逼近于1时,这个极限的精确值是多少。这意味着在原来的图像上极限点的高度为−π/2。
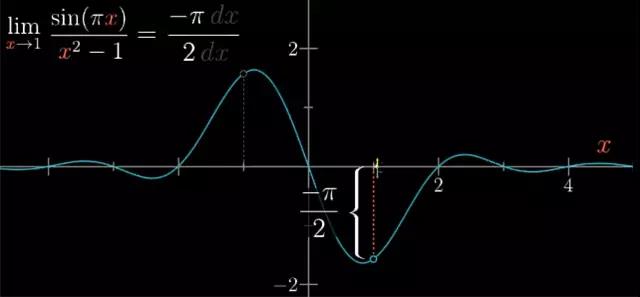
图26
刚才讲的针对性有点强,所以我想用更普世的方法再讲一遍,考虑任意两个函数f(x)和g(x),他们在在x=a的值均为0。这两个函数唯一的约束条件就是它们在x=a点可导——意味着在无限放大之后,它们可以被看作是直线。
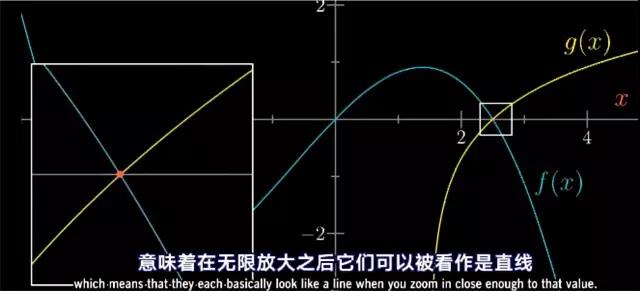
图27
因为他们在这个点的值均为零,所以不能直接计算f(a)/g(a)的值。但可以取x离a十分相近的值,求x逼近a时候的极限值。即df/dx在a点的值,再乘上dx。同理,g在这个点的值大约是(dg/dx)*(a)*dx。
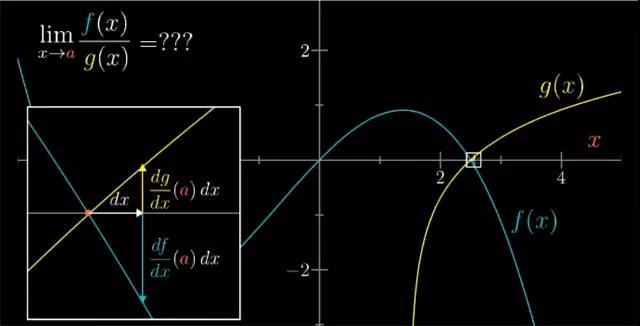
图28
所以在这个点函数f(x)和g(x)的输出之比应该是下式:
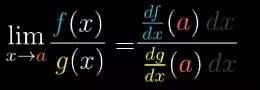
图29
由于上下dx抵消了,所以这个比值几乎就与f和g导数值之比相等。变化量dx取得越小,这个比值就越精确。所以这个比值就等于极限值的精确值。在计算极限时,这是一个很方便的技巧。
当你需要计算某些0/0型的极限时,可以对分子分母分别求导,然后再把数代入。
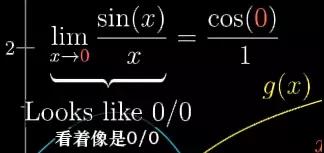
图30
这个神奇的技巧就叫做“洛必达法则”(L'Hôpital's Rule)。有趣的是,这个技巧其实是由约翰.伯努利发现,但洛比达是个土豪,花钱冠名了伯努利的一些数学成果。
下期视频,会介绍积分是什么?同时讨论一下微积分基本原理,积分和导数一样,也是要借助极限来解决“无限”带来的困惑。
图31
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











