来自3Blue1Brown《微积分的本质》视频:https://space.bilibili.com/88461692
(点击最下阅读原文查看B站更多精彩内容)这里特别感谢各位翻译的贡献:昨梦电羊,罗兹,Solara570,圆桌字幕组等。有意的译者请移步B站进行联系!
微信公众号【遇见数学】根据视频内容整理文字版,方便各位同学学习,先来看下视频吧。
视频1
这次我们来看看二阶导数,设函数为f(x),那么导数可以理解为x点处所对应的图像的斜率。图像很陡对应导数的值很大,向下倾斜说明导数是负的。
而二阶导数是导数的导数,它表示斜率的变化情况。最直观的方法就是观察f(x)曲线的弯曲方向,让它向上弯曲,斜率在增加,这时二阶导数就是真的。
当它向下弯曲斜率再减少,二阶导数就是负的。
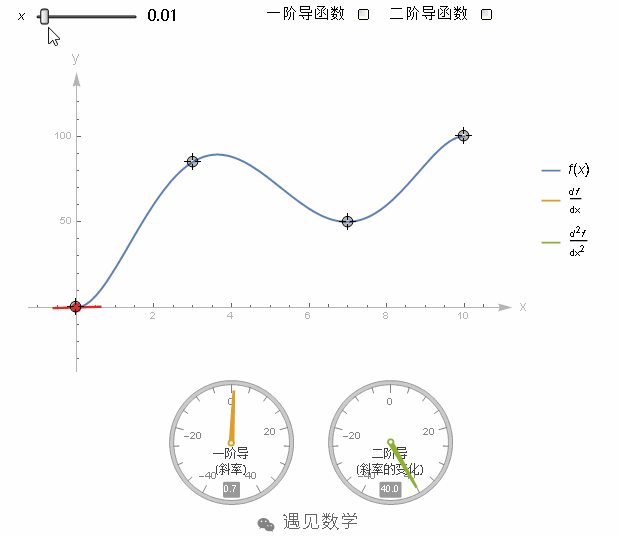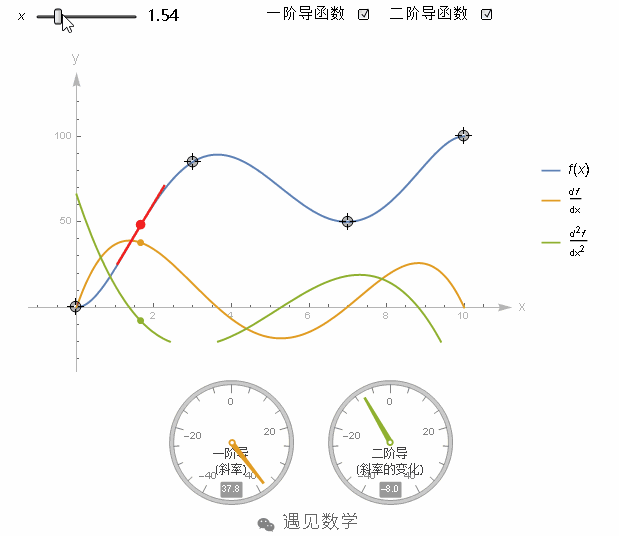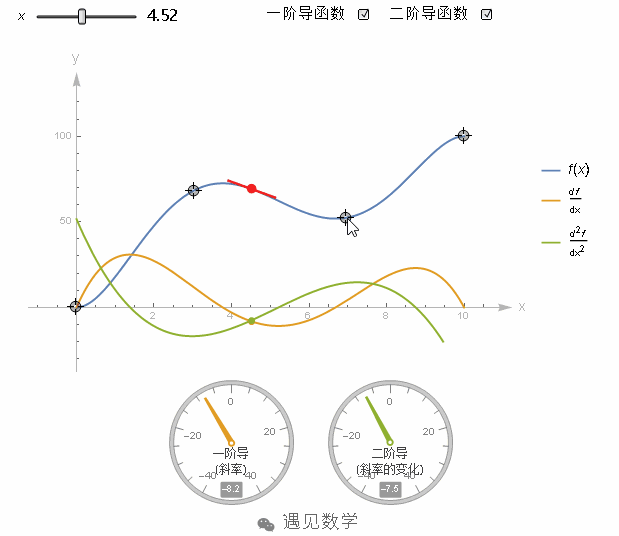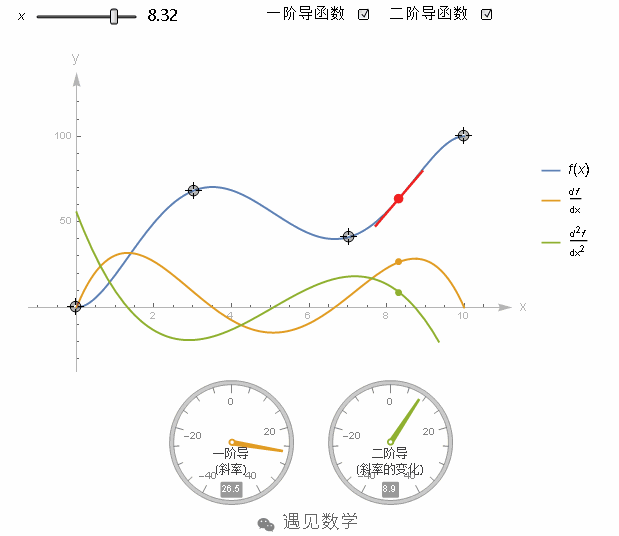
图1
比如这个函数在x=4时,它的二阶导数是一个很大的正值,因为此时函数的斜率在快速增加。而这个函数,在x=4的时候,他的二阶导数依然为正,但相对刚才a=5时就小了,因为它的斜率增加的很慢。在图像没有弯曲的地方,二阶导数就是0。
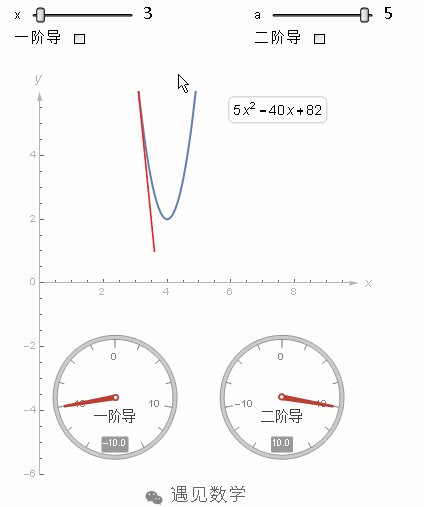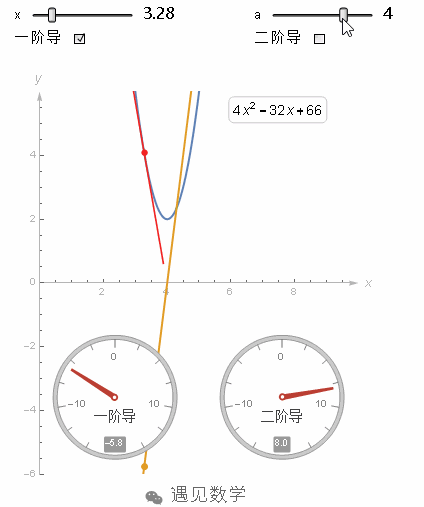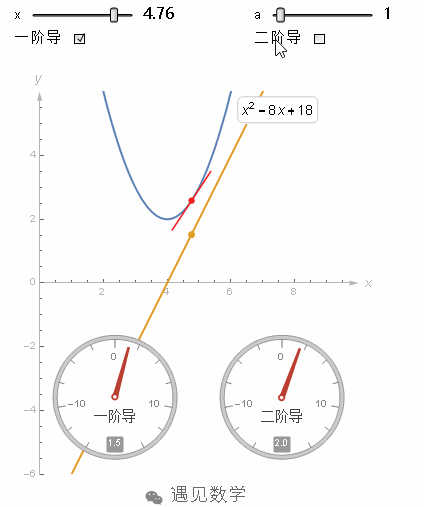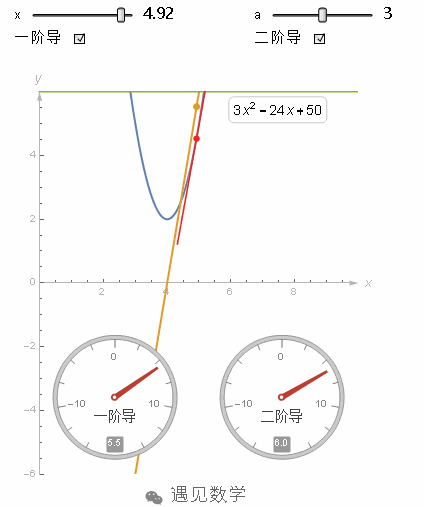
图2
这符号它倒是可以被写成这样:
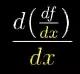
图3
表示想求导数的微小变化除以x的微小变化,这表示要让这里的两个dx都趋近于0。嗯,或者是按标准写法把它缩写成:
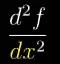
图4
考虑怎样理解二阶导数符号的解读,考虑函数在x处,然后向右连续增加两个小的增量dx。这个重量使得函数增加了,第一个变化量我们把它叫做df1,第二个增量同理,但造成的变化量会些许不同,我们把它叫做df2。
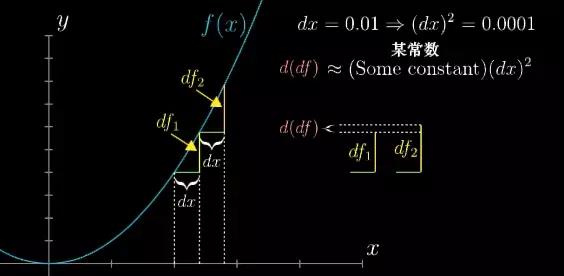
图5
这两个变化量之间的差,也就是函数变化量的变化量就叫做d(df)。
你应该把d(df)当做一个非常微小的数,它和dx2成正比。所以如果你带入dx=0.01的话,那么d(df)就应该大约和0.0001成正比。
二阶导数就是变化量的变化量比上dx2,更准确的说是dx趋近于0的时候,这个比值的极限。

图6
尽管d并不是一个能和f直接相乘的变量,但是为了使记号更简单,写成下面的形式:

图7
实际问题中的加速度是帮助你理解二阶导数的最佳例子,假设物体沿直线运动,并且你有一个它的距离—时间函数,或许它的图像看起来就是像下面这样,随着时间的持续的增加。
它的导数就是每一时间点的速度,其实导数的图像就像是个小山包,先增加到一个最大值,然后减小到 0。
所以二阶导数能告诉你在某个时间点上速度的变化率,这就是加速度。
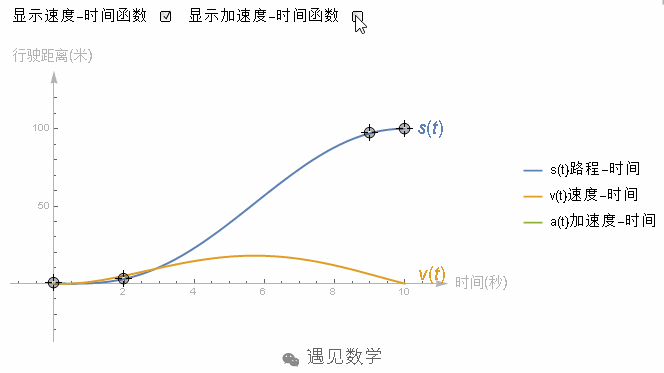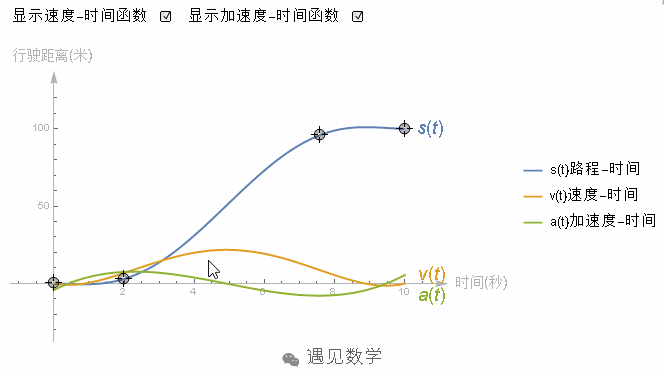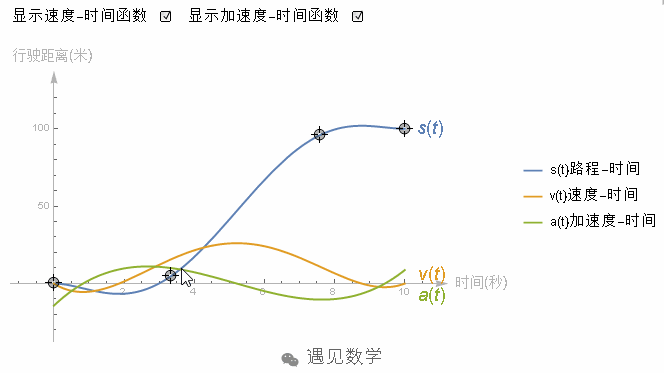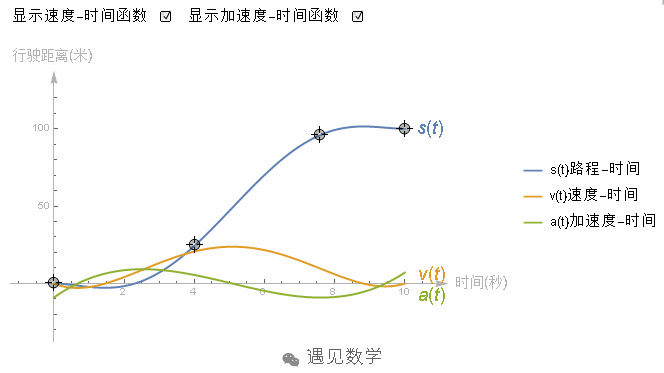
图8
在这个例子中,前半段路程二阶导数是正的,说明车在加速。后半段二阶导数是负的,说明的速度在减慢。
三阶导数就叫做急动度(Jerk),如果急动度不为0,那么说明加速度本身在变化。
高阶导数最大的作用就是帮助我们得到函数的近似,这就是我们下集要讨论的泰勒级数。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











