
图1

图2
希尔伯特旅馆悖论(Hilbert's paradox of the Grand Hotel)是一个与无限集合有关的数学悖论。在上世纪20年代,德国数学家大卫·希尔伯特提出了一个著名的思想实验来向我们表明,用人类的思维去把握“无穷/无限”这个概念究竟有多难。

图3
假设有一个拥有可数无限多个房间的旅馆,且所有的房间均已客满。或许有人会认为此时这一旅馆将无法再接纳新的客人(如同有限个房间的情况),但事实上并非如此。
一、来了有限个新客人
想象一家旅馆有无穷多间客房,还有一位非常勤奋的夜班经理。一天晚上,无限旅馆彻底客满,已经被无限多位客人全部预定了。一个男士走进了旅馆并且要求一个房间。夜班经理并没有拒绝他,而是决定给他一个房间。
怎么可能?很简单,他让1号客房的客人搬到了2号客房,2号客房的客人搬到3号客房,以此类推。每个客人从"n"号房间搬入"n+1"号房间。

图4
因为旅馆有无限个房间,所以总有第n+1个房间给每n个已入住的客人,这样的话1号房间就留给了新的客人。
这个安排房间的方法可以被重复给任何有限个的新客人们。假设一个观光大巴有40个乘客下车要找房间,那么每个已在的客人只要从"n"号房间搬到"n+40"号房间,因此,就能有新的40个房间供入住。

图5
二、来了无限个新客人
但是现在有一个无限长的巴士拉了可数的无限多位客人来订房间。关键是可数无限个新客人。

图6
现在,这个无限长的巴士里面搭乘的无限多客人一开始为难了夜店经理,但是他意识到有一个方法来安置每一个新人。他让1号房间的客人搬到了2号房间。他然后让2号房间的客人搬到了4号房间,3号房间的客人搬到6号房间,以此类推。让每一个原先入住的客人从"n"号房间搬到了"2n"号房间,于是只有无限多的偶数号房间里住了人,而空闲下来的无限多个奇数房间由新来的客人入住。
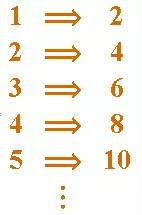
图7
通过这样安排,这辆无限长的巴士的乘客们将占用这些奇数房间。皆大欢喜,旅馆的生意达到了空前的兴隆,人们从世界各地蜂拥而来。
三、无限个大巴且每个巴士有无限客人
一天晚上,发生了超乎想象的事情发生了。夜班经理看了外面并且看到了由无限多辆并且每一辆都是无限长的大巴们开到旅馆门口,每个大巴都载着可数的无限多位的客人。

图8
如果当班经理不能给这些疲惫不堪的乘客找到房间住下来,这个旅馆就要失去无限多的收入,并且他肯定会失去工作。幸运的是,他记得在公元300年前,Euclid给出了质数有无穷多个的证明。

图9
所以,为了完成这个看上去不可能实现的任务:找到无限张床,给无限辆的大巴上的无限位疲倦的旅客们。夜店经理安排给每个原有的客人这样调整一下房间。

图10
把第一个质数2作为的底数,原有客人当前的房间号为指数。譬如,原先住在房间号为7的旅馆客人,就要搬到房间号为2的7次方的房间里,也就是128号房。
然后,夜班经理这样安排在第一个超级大巴上的客人,以下一个质数3为底数,以他们在大巴的座位号为指数来分配房间。

图11
因此,座位号为7的第一辆大巴上的人到房间号为3的七次方即2187号房间去。这个过程持续给第一辆大巴上的所有人。
第二辆大巴上的乘客们被安排到了下一个质数5为底数。

图12
接下的大巴以7为底的幂。每辆大巴如下:11的幂,13的幂,17的幂,等等。因为这些底数都是质数,因此就房间号就不会重复,也就利用了这种基于质数的独特安置方案就能将所有大巴里乘客们散列分配到到各自房间。

图13
这样一来,夜班经理能够安排每辆大巴的每位乘客入住。尽管,还有许多房间是空的,像是1,6,10,12号房因为不是任何质数的幂就闲置了起来。不过幸运的是,他的老板数学不是很棒,所以的夜班经理的工作还是保住了。
夜班经理现在都是面对这些难题都只涉及到了最低级的无穷数,主要是可数的无限自然数1,2,3,4……等等。George Cantor称这个等级的无限为阿列夫—零(Aleph-zero)。

图14
我们使用自然数为房间号,同时也是使用自然数来对应大巴的座位号。如果我们处理更高级的无穷数,比如实数的无限情况,前面这些结构策略就不行了,因为我们没有办法系统地包含每一个数字。比如实数,负数,无理数这样的场景,都在提醒我们目前这样相对有穷的思维,如果想要掌握无穷数这样的概念是有多么困难。或许你在希尔伯特旅馆好好睡了一晚后能解决这些问题。不过老实说,夜班经理可能需要你在凌晨2点换房间。

图15
根据有关TED Ed视频:The Infinite Hotel Paradox及维基百科编写。完整视频见【阅读原文】链接(需翻墙),或微信后台回复关键字 [TED] 得到国内云盘下载地址。更多TED Ed视频见下图或未来继续推出的文章。

图16
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











