直接看TED Ed原汁原味的演讲,或者看下面我编写的文章,因为除了我理解视频主要内容,更加入了自己的一些体会和想法,还请各位老师和朋友多多指教和交流讨论。
「予人玫瑰, 手留余香」
如果感到本文有些许帮助,感谢转发,支持本号更快发展!请加本人微信Math79,让我有幸认识曾经帮助过我的您!
视频1
希帕索斯,生活于大约公元前500年,生卒年月不详,属于毕达哥拉斯学派门生。

图1
公元前5世纪,毕达哥拉斯学派认为“万物皆数”,世界上只有整数和分数(有理数)。而希帕索斯却发现了令人震惊的“无限不循环小数”,即无理数,令该学派感到恐慌,并引发了第一次数学危机。有传言说最终希帕索斯被自己的老师毕达哥拉斯(Pythagoras)判决淹死。
一、被惩罚的哲人
正如希腊神话中许多英雄一样,哲学家希帕索斯(Hippasus)被传说要接受神的惩罚。

图2
但他错在哪儿了呢?是他杀人了,还是他破坏了神圣的仪式。都不是!希帕索斯的罪源于一个数学证明——无理数的发现。
希帕索是毕达哥拉斯学派中的一员,他们对于数字有着宗教般的崇敬。

图3
他们的格言“万物皆数”(All is Number):暗示着他们认为数字是宇宙建立的基石,而且他们也相信任何事物从宇宙研究到音乐发展,从形而上学到道德观念归,根到底都是数字比例的问题。

图4
因此,任何数字都可以被写成一个比例形式(分数)。
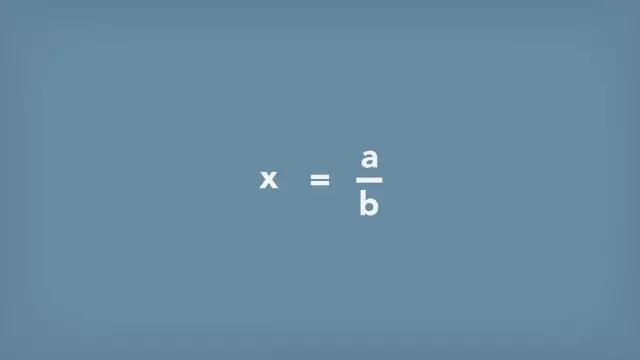
图5
5就是5/1,0.5就是1/2等等,甚至一个可以被无限延伸的十进制数字,也可以被准确表示成34/45。
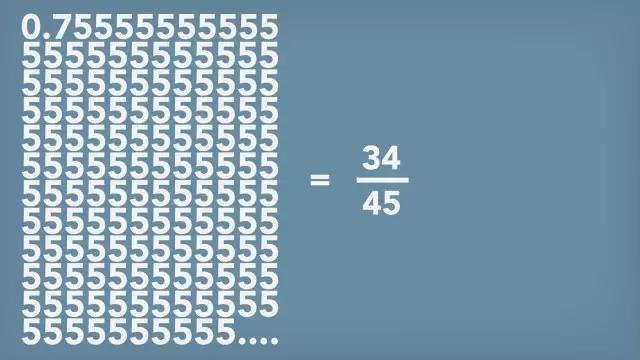
图6
这些数字都被称为有理数(Rational),而希帕索斯却发现了一个背离这种和谐规律的数字——一个本不该存在的数字√2。

图7
二、反证法证明存在着无理数
这个问题起源于一个非常简单的图形一个四边长度均为单位1的正方形。
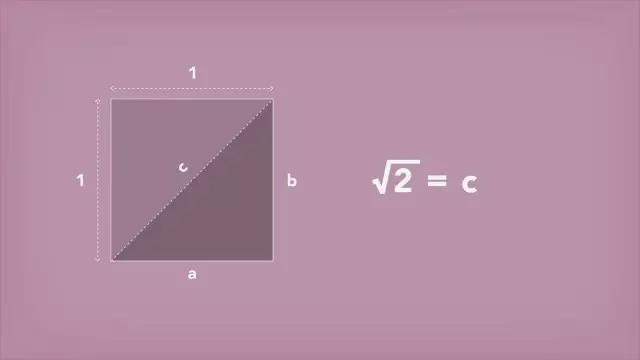
图8
根据毕达哥拉斯的理论这个正方形的对角线长度应该为√2,但是无论希帕索斯如何尝试都不能将√2 变为两个整数的比例形式。他并没有选择放弃而是决定证明这个数字确实无法被比例表示出来。
希帕索斯首先假设毕达哥拉斯的“万物皆数”的观点是正确的,√2是可以被表示成两个整数之比。

图9
他假设这两个整数分别为p和q,并假定这个比例已经被最简化。因此,p和q应该没有相同公约数,要证明√2并不是有理数,希帕索斯只需要证明p/q并不存在即可。

图10
他将等号两侧均乘以q,然后两侧均计算平方,这样得到了一个等式。
任何数字乘以2的结果都是偶数,所以p的平方是偶数如果p是奇数,则p的平方不可能为偶数因为奇数乘以本身,得到的还是奇数,所以p也应该是一个偶数。因此,p可以表示为2a,其中a也是一个整数。把这个等式带入原来的方程,并简化得到:q^2=2a^2。再一次,任何数字乘以2得到的结果为偶数,所以q的平方一定是偶数,那么q也一定是偶数,这就得到p和q都是偶数的结果。
但如果这是正确的话p和q就有一个共同的因子2,这就跟最初的题设矛盾!!

图11
至此,希帕索斯得以证明,这样的比例是不存在的,这被称为矛盾证明法。而根据传说上帝并不喜欢矛盾的存在。
三、无理数可以画出来
有趣的是,即便我们无法将无理数表示成为整数的比例形式,我们却可以将它准确表现在图形之中,以√2为例。我们需要做的就是准确的画出一个两条直角边均为单位一的三角形,他的的斜边的长度就是√2。
这同时也可以被延伸下去,我们可以继续画另外一个直角三角形,其中一条边以刚才的斜边为基础,另一条边长度为单位1,这个三角形的斜边程度就是单位√3。
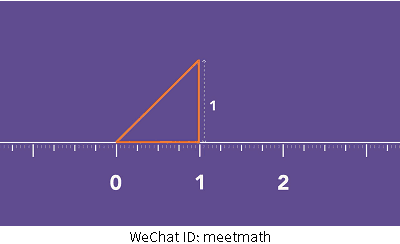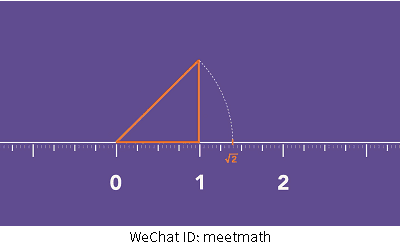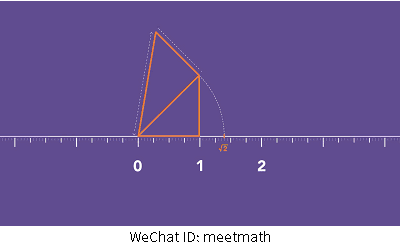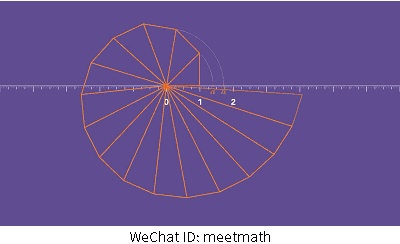
图12
它同时还可以继续被延展下去,关键问题是小数和分数都只是表现数字的方法之一,√2只是一个边长为单位一的直角三角形的斜边长度罢了相似的。
著名的无理数π也是与它描述的图形关系,一样代表者圆周长和半径的比例,近似值22/7或者355/133是永远无法准确的表达出π值的。

图13
我们永远也无法知道在希帕索斯身上到底发生过什么,但是我们知道他的发现引发了第一次数学危机并激励更多数学家继续前行,所以无论神话里面怎么说,永远不要害怕去探索不可能!
根据有关TED Ed视频:The Infinite Hotel Paradox及维基百科编写。完整视频与字幕,微信后台回复关键字[TED]得到国内云盘下载地址。更多TED Ed视频见下图或未来继续推出的文章。

图14
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











