
图1
欣赏TED-Ed原汁原味的演讲,或者看下面【遇见数学】编写的文字版。
视频1
一、叔叔的遗嘱
你有钱又古怪的叔叔去世了,你和你的99个恶心的亲戚被邀请到他遗嘱的宣读会。他想要把所有钱留给你,但他知道如果他这么做了,你的亲戚会永远纠缠着你。

图2
所以他只能寄希望于他教给过你的所有猜谜技巧。
你叔叔在遗嘱中写道:“我设计了一个谜题。如果你们100个人最后共同解开谜题点话,就100个人均分我的钱。但是,如果你是第一个动脑筋就找到答案解决问题的人,你将会独享我的所有遗产。祝你好运。”
二、柜子谜题
律师把你和99个亲戚带到了宅第的密室。这有100个储藏柜,每个柜子里藏着一个词。

图3
他说:“每个亲戚被分发1到100里的一个数字。”1号继承人要打开每个储藏柜。

图4
2号将关上偶数号码的储藏柜。

图5
3号改变整除3的储藏柜的状态,如果储藏柜开着,那就关上,如果储藏柜关着,那就打开。

图6
往下所有人都按这个规律执行。最终开着的柜子里所留下所有单词就是保险箱点密码。

图7
就在1号继承人开始打开柜子之前,你就大步向前告诉了律师哪些柜子会是开着的。怎么做到的呢?如果你想自己找出答案来,就暂停往下翻页,思考一下。

图8
三、整个的过程
可以先来看下整个过程吧。

图9
答案关键是算出每个柜子被改变状态的次数,这是和柜子号码的因子数目相同的。比如对于6号柜子,1号继承人把它打开,2号把它关上,3号把它打开,最后6号把它关上。1,2,3,6就是6的四个因数。

图10
所以如果一个柜子有偶数个因数,它最后就一定是关着的。如果一个柜子有奇数个因数,它就是开着的。
大多数柜子有偶数个因子因数,因为因数自然是成对出现的。
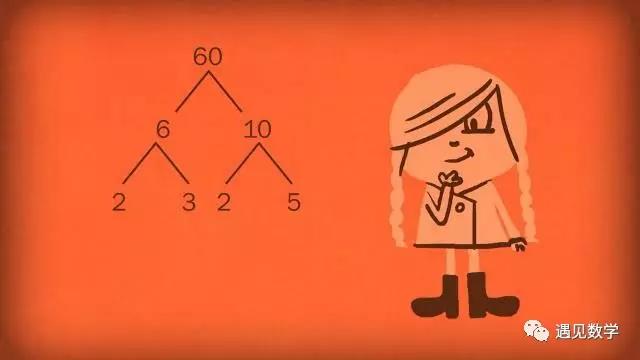
图11
实际上,仅有的几个有奇数个因数的柜子是完全平方数(Square number)。
因为它们有一个因数是自己乘自己,比如对于9号柜子,1号继承人把它打开,3号把它关上,最后9号把它打开。3x3=9。但是3只能算一次动作。
因此,每个完全平方数柜子最后是开着的。你知道了这十个柜子就是答案,所以你立刻打开了它们。

图12
里面组合起来是一句话,写着:“保险箱的密码是前五个只被碰了两次的柜子。”

图13
你发现满足条件的一定顺序为质数的柜子,因为它们每个只有两个因数:1和它本身。
所以密码是2-3-5-7-11。律师把你带到保险箱前,最终你获得了你叔叔的所有遗产。

图14
根据有关TED Ed视频:Can you solve the locker riddle?及维基百科编写。完整视频与字幕,微信后台回复关键字[TED]得到国内云盘下载地址。更多TED Ed视频见下图或未来继续推出的文章。

图15
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











