欣赏由【遇见数学】提供带字幕视频,或者看下面【遇见数学】编写的文字版。
视频1
谁想要那么多位的π?想要给多大的房间糊墙啊?以下是5个理由,说明那么多位Pi的重要性,不过这些理由也并不都是合理的。
一、为科学测量提供精确性
这可能是我听过最没脑子的理由了。宇宙的直径是930亿光年,氢原子直径大约0.1纳米。
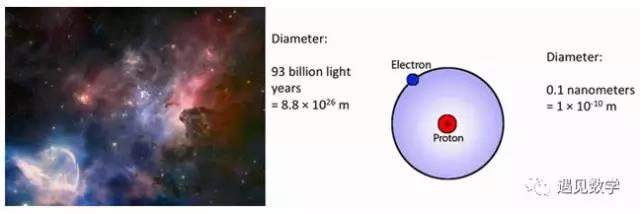
图1
所以只要知道39位的π,就足以精确地的告诉你环绕整个宇宙需要几个氢原子了。

图2
而任何力学计算只要5位数就绰绰有余了。
二、看看我们能走多远是很棒的事
确实有些壮举是在探索的名义下做出的,不过这种“因为它就在哪里”的期望虽然很诱人,但仅仅因为我们能够探索某样东西,并不表明它有价值。

图3
比如在π的761位后面可以找到费曼点(Feynman Point)——这里有6个连续的9。但……谁在乎?!其他连续的数字也能找到,然后并没有数学意义。

图4
三、计算机完整性
π的数位有助于检验和开发新的算法,金田康正借助这两个公式,生成并核对了超过一万亿位的π值。

图5
经过这么多算术运算和数据传输,还能保持一致,这是计算机运转无误的有利证据。计算π的一个副产物是开发了快速傅里叶变换,是数字信号处理中一件突破性的工具。
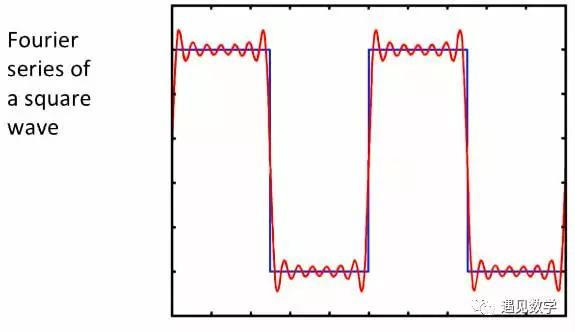
图6
四、提供证据π是正规数
正规(normal)的意思其中任何一串数字以期望的频率出现。例如,期望红色数字4出现的次数占10%。或数字串28的出现次数占1%。要证明一个数是正规数极为困难。但π的正规性可以从这张表中看到证据。每个数字都出现大约1000亿次。
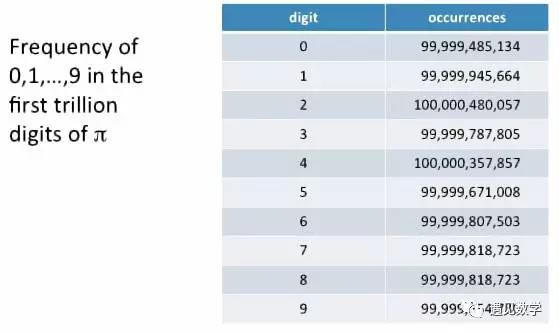
图7
数的正规性为什么重要?正规数可以用来模拟随机数生成器,这张图显示了用10进制的π数字生成的随机游走。从原点出发,根据下一个数字决定朝0~9数字对应的10个方向中的哪一方向移动一步,下面是π的500位游走动画。

图8
再来看10000位的游走图片:
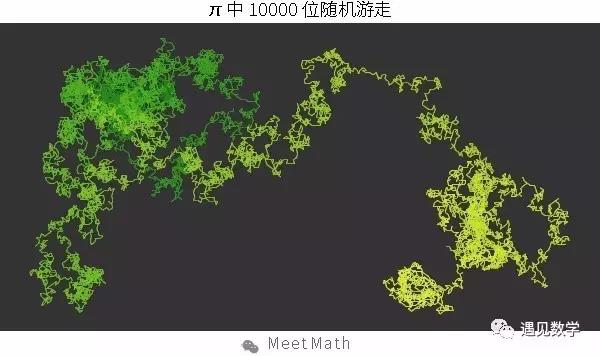
图9
五、更多位的π能帮助我们理解素数
π与素数有密切的关系,这个无限乘积名叫欧拉乘积,包含了π和全部素数。

图10
拥有的素数越多,就能越精确地逼近π。

图11
而这类公式有无限多个。

图12
利用这些公式能不能从高度精确的π值计算出大量素数呢?

图13
这个问题还有其他的问题都可以把素数跟π联系起来。
那么你会用那么位的π来做什么呢?这是个值得考虑的问题。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











