欣赏由【遇见数学】提供视频,或者看下面整理编写的文字版。
视频1
Let's Make a Deal是以前红极一时的电视节目,所有人都可以报名参加,最后赢得人可以把车开回家。当时的主持人蒙提·霍尔(Monty Hall)也是红得发紫。

图1
蒙提给你个机会,让你选一扇门,我们把门记为门1,门2,门3。
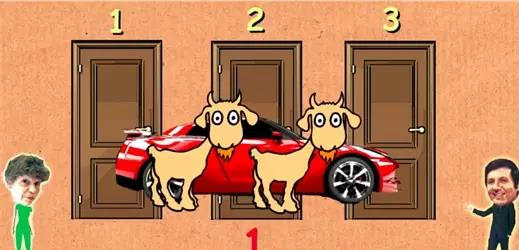
图2
三扇门中之一藏着节目的大奖——一辆红色的跑车。而两扇门后则是山羊,当然你肯定选择汽车。看上去你只有1/3的概率中奖。
假设你选择了门1,这是蒙提会重复他的老一套,他会打开一个你没选的门,也就是门2或者门3。假设他打开门2好了,而后面是一只山羊。当然,他原本知道门2后面就是山羊。

图3
然后他会幽幽的看着你,然后问:“你还坚持你的选择吗?现在只有门1和门3两个选择。”所以你要么坚持选择门1,要么改选了门3。
这时候许多选手会犹豫,因为他们获取了新的信息。有一点值得注意的是,这个问题总是使人们争论不休,节目播出的那段时间里并没有人声称“这个游戏有绝佳的策略”。
但事实上是有一个更好的策略——你在这种情况下,必须要调整选择,选择门3。也就是说每次遇到这种情况,你必须得换,这就是最佳策略。
来分析一下,你开始只有1/3的概率选中跑车,也就是说剩下2/3能中奖的概率由后面两个门承担。但是我们又知道门2后面不会是车。
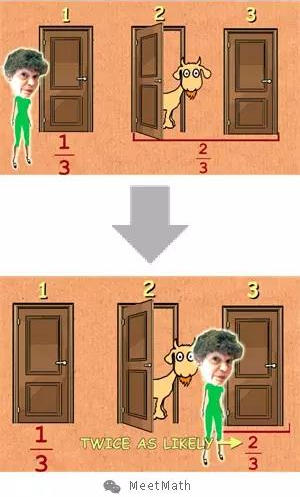
图4
所以门3后面就有2的概率是车。所以你才应该调整选择,选择赢得跑车概率较大的门3。
当然,如果换了的话也不一定肯定会赢,因为毕竟还有1/3的概率会输,但是如果你反复玩这个游戏的话,那么将会发现将近2/3的次数你都会赢。所以你不得不承认换门是绝佳的策略。下图就是按照最佳策略模拟1000次的图形,可以看到中奖概率会逼近2/3的地方。
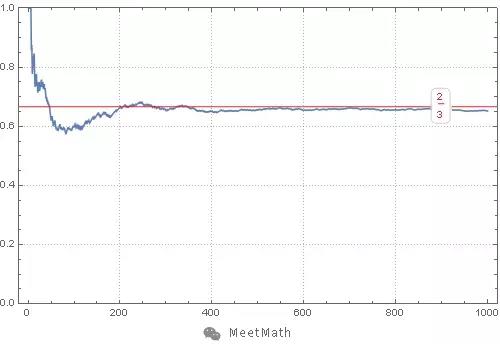
图5
你可以认为门2和门3刚开始承担的2/3中奖的概率,最后则集中到了蒙提没有打开的门3上。这就是实际的结果,也就是直观的结论。
还有一种更牛B的思路,我们把情况推广到100扇门,然后再来玩儿这个游戏。

图6
蒙提还是只让你打开一扇门,跑车还是藏在其中1扇门后,但是99扇门后面都是山羊。
现在我们选一下门,还是假设选门1好了,这次你可能想得和只有三扇门的时候不一样,原来你就有1/3 的概率赢,而现在只有1%,所以跑车非常可能在剩下的99扇门里面,这时候蒙提打开了99扇门中的98扇。这98扇门后面全是山羊,他再问你换不换?

图7
从100扇门的角度来看结果是显而易见的,这样当门变得多了,你明白了99%的概率是跑车停在99扇门中但蒙提没有打开的最后那扇门后。这时你肯定会决定换门,最终也就很可能把跑车开回家了。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











