来自Numberphile《The Josephus Problem》,这里特别感谢圆桌字幕组奉献。
微信公众号【遇见数学】根据视频内容整理文字版,方便各位同学学习,先来看下视频吧。
视频1
本期要讲的是被称为约瑟夫问题,这个问题是有历史根据的。一群犹太士兵被罗马军队包围,他们不想被抓获,所以他们决定采用某种方式来避免被俘虏或自杀等等。他们会围坐成一个圈,第一个人会杀了他的左侧的人。下一个还活着的人又会用剑杀死自己左边还活着的人,这样以此下去,然后最后一个人当然只好自杀了。

图1
但事实上是比起自杀,约瑟夫还是更愿意被俘虏。但他担心,如果他坦白的话,他会成为众矢之的。所以他想找出其中规律,他应该在圈子中他应该坐在哪里,好让自己成为最后活下来的那个人,然后他会投降,而不是选择自杀。
推而广之的话,问如果有n个人的话,坐在哪个位置才能最终存活呢?这个问题有点棘手,所以让我们缩小问题的范围,动手计算并寻找其中的规律。例如,让我们列举出前80个人的所有情况。下面列出一个表格,n为座位总数,W(n)是最终胜者的座位。

图2
可能你会最先注意到,最后所有的幸存者都是奇数,原因也很简单,因为早在第一轮的时候,偶数位置的人已经全部被杀死了。所以,这是最开始的规律。
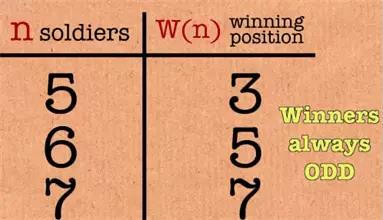
图3
我们已经开始看到规律,并能做出预测了。视频主角当年教授告诉他的学生:“如果你知道一些东西,那就去证明它,并确保你已经了解透彻了那部分,而这通常可以揭开剩下的谜团”。所以现在来尝试设立一个猜想,并证明理论。
我们的猜想是:如果n是2的幂,那么获胜的席位就是1。
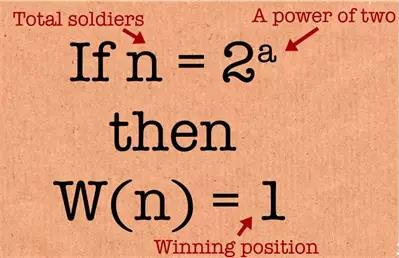
图4
经过类似递归的计算验证我们可以确信,有2的n次个士兵会发生什么。那么我们怎么解释,士兵人数在2的幂之间的时会发生什么(也就是4~8,或者8~16……)。或者我们绘出去1~300名人数最后获胜席位的情况,先观察图形一下是否存在着某种规律,从下图来看是有着某种重复的模式:
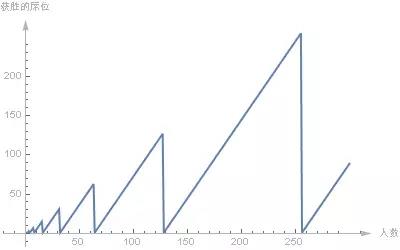
图5
我们来观察士兵人数为4和8之间的结果,它以2位间隔上升。那我们怎样来解释中间这个以2递增的现象呢?可不可以将任何数字写成一个较大的2的次幂,加上另一个数,提取这个数字中可以找到的最大的2的次幂,剩下的数会比那个2的幂小一些。

图6
当你用二进制来表示数字时,是一串0或1组成的,也可以将这个数写成很多2的幂相加,只需要挑那个最大的就可以了。比如77,最大的2的幂是64,可以写成77=64+8+4+1的形式。

图7
77可以写成2^6+l的形式,而l会告诉我们在2的幂中间会有哪些奇数出现,再比如13。
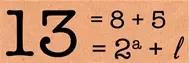
图8
或者说当已经杀掉5个人后,剩下的人数刚好就是2的幂。
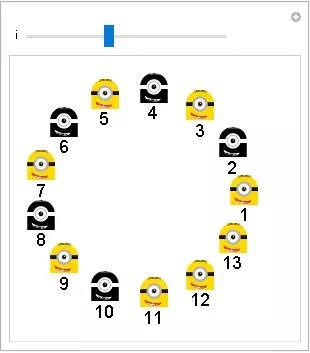
图9
而我们知道有2的幂个士兵时,胜者是最先动手的人,所以从上图来看下一个要动手的人(即11号)会获胜,这就是通向最终答案的关键。那就是说,如果你将你的数字写成2^a+1的形式,经过l步后,轮到下个动手的人就会赢,因为去掉l个人,就会剩下2的幂个人。而获胜者的座位就可以用2l+1来表示。
所以这个定理就是下面的定义形式:
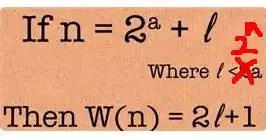
图10
可以验证这个结论适用于所有的答案。
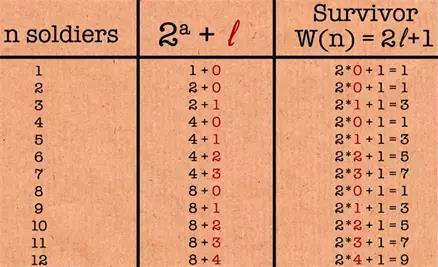
图11
我们已经阐述了其中的机制,那就是l步后,剩余的人数是2的幂,那么会轮到第2l+1个人会赢。
在这个问题里的答案还可以用二进制来解释,当我们把一个数写成2的幂求和时,就可以用二进制来表示。
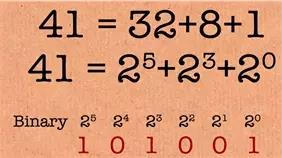
图12
这里就有一个解决约瑟夫问题的捷径,将整个二进制数左移一位,然后再转成十进制就是最后的答案(其实就是找到l,并求2^l+2^0的过程)。所以在二进制中,这是一种超级简便的方法,能从n直接算出答案来。
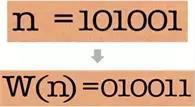
图13
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











