
图1
微积分是近代数学中最伟大的成就,对它的重要性无论作怎样的估计都不会过分。——冯·诺依曼
一、287年:阿基米德的“逼近法”
“给我一个支点,我可以撬动地球。”
对数学和物理学的影响极为深远,被视为古希腊最杰出的科学家。他与牛顿和高斯被西方世界评价为有史以来最伟大的三位数学家。
他利用“逼近法”算出球表面积、球体积、抛物线、椭圆面积,后世的数学家依据这种方法加以发展成近代的“微积分”。

图2:1620年费地的布面油画《沉思的阿基米德》
二、263年:刘徽注释《九章算术》
东方古代数学泰斗
用割圆术计算圆周率,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”。

图3
求得圆周率的近似值为3.14,这种极限思想和无穷可分甚至是古希腊数学不能比拟的。

图4
三、1088年:沈括著《梦溪笔谈》
中国科学史上的重要文献
北宋的沈括所著百科全书式的著作,因为写于润州(今镇江)梦溪园而得名,收录了沈括一生的所见所闻和见解。内容涉及天文、数学、物理、化学、生物、地质、地理、气象、医学、工程技术、文学、史事、美术及音乐等学科。书中开创了“垛积术”(高阶等差级数求和),“会圆术”(求出弧长的方法)。“棋局都数”的研究则暗用了组合方法和指数定律。

图5
四、1629年:费马
“我发现了一个美妙的证明,但由于空白太小而没有写下来。”
皮埃尔·德·费马法国律师和业余数学家(不过在数学上的成就不比职业数学家差)。费马引理给出了一个求出。可微函数的最大值和最小值的方法。因此,利用费马引理,求函数的极值的问题便化为解方程的问题。
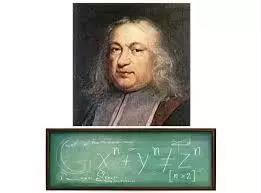
图6:费马及费马最后定理
五、1637年:笛卡尔
“我思故我在。”
勒内·笛卡尔,法国著名哲学家、数学家、物理学家。对数学最重要的贡献是创立了解析几何。笛卡尔成功地将当时完全分开的代数和几何学联系到了一起,他向世人证明,几何问题可以归结成代数问题,也可以通过代数转换来发现、证明几何性质,为后人在微积分上的工作提供了坚实的基础。

图7
六、约1150:婆什迦罗
印度数学的最高成就
婆什迦罗,印度古代和中世纪最伟大的数学家,天文学家。对数学主要贡献:比牛顿和莱布尼茨早五个世纪就构想了微积分;采用缩写文字和符号来表示未知数和运算;他广泛使用了无理数,并在运算时和有理数不加区别。

图8:婆什迦罗及他设计的永动机
七、1665年:牛顿与《广义二项式定义》
“如果我比别人看得更远,那是因为我站在巨人的肩上。”
艾萨克·牛顿,英格兰物理学家,数学家,天文学家,在老师巴罗的指导下,1665年发表广义二项式定理,并开始发展一套新的数学理论,也就是后来为世人所熟知的微积分学,牛顿称之为“流数术”。

图9
八、1670年:伊萨克·巴罗《几何学讲义》
“一个爱书的人,他必定不致缺少一个忠实的朋友,一个良好的老师,一个可爱的伴侣,一个优婉的安慰者。”
英国著名数学家,1670 年发布的《几何学讲义》包含了他对无穷小分析的卓越贡献,特别是其中“通过计算求切线的方法”,十分接近微积分基本定理,微积分的最终制定后来由其学生艾萨克·牛顿完成。

图10:伊萨克·巴罗(1630年—1677年)
九、1684年:莱布尼茨关于微分学的第一篇论文
“世界上没有两片完全相同的树叶。”
戈特弗里德·威廉·莱布尼茨,德意志哲学家、数学家,获誉为十七世纪的亚里士多德。
在数学上,他从几何角度和牛顿先后独立发明了微积分,1684年发表了第一篇微分学论文《一种求极大值、极小值和切线的新方法,它也适用于有理量与无理量以及这种新方法的奇妙类型的计算》 ,他所发明了微积分的数学符号dx,dy和∫被更广泛的使用。

图11:莱布尼茨(1646年—1716年)
十、1691年:约翰·伯努利著世界上第一本关于微积分的教科书
瑞士的伯努利家族是世界颇负盛名的数学世家
雅各布和弟弟约翰·伯努利是莱布尼茨的朋友,他们不但迅速掌握了莱布尼茨的微积分并加以发扬光大,而且是最先应用微积分于各种问题的数学家。

图12
洛必达法则纠纷
有一段时间,伯努利被洛必达聘请为私人数学老师。伯努利签了一纸合约。这合约给予洛必达特殊的权力,准许洛必达发表伯努利所有的研究。洛必达最先地写成了一本的微积分教科书《用于了解曲线的无穷小分析》,其内容大多是伯努利的杰作,包括现世知名的洛必达法则。
十一、1755年:欧拉著《微积分概论》
将微积分带大成人
欧拉,18世纪最杰出的数学家之一,同时也是有史以来最伟大的数学家之一。欧拉实际上支配了18世纪至现在的数学;他是历史上最重要的求积专家之一,被积函数越是奇特,他做的越是得心应手;他完善和扩展了微积分,为无穷级数,微分方程等分支的发展奠定了基础。

图13:欧拉
十二、1823年:柯西的《无穷小分析教程概论》
“不要让几何直观,蒙蔽了我们的双眼。”
柯西在微积分历史上影响颇深,他认为全部微积分应当建立在极限思想的基础上:“当属于一个变量的相继的值无限地趋近某个固定值时,如果最终同固定值之差可以随意地小,那么这个固定值就称为所有这些值的极限。”

图14:柯西
十三、1815年:魏尔斯特拉斯与ε-δ定义
现代分析学之父
德国数学家魏尔斯特拉斯进一步的严格化,给函数的极限建立了教科书中一直沿用到今天严格的ε-δ定义,来代替柯西的“无限趋近”描述,使极限理论成为了微积分的坚定基础,系统建立了实分析和复分析的基础。

图15:魏尔斯特拉斯
微积分学至此基本发展完善。
古代中国数学在微积分方面已经积累了非常多重要成果,但遗憾在元朝之后,八股之害抑制了科学上继续前进可能,在系统创建微积分的大门前停下了步伐,实在让后人无限感慨!
如果对微积分历史有兴趣,可以继续阅读图灵出版的《微积分的历程:从牛顿到勒贝格》,学到非常有意义的数学知识以及更多证明,文末点击【阅读原文】跳转此书详细介绍页面。

图16
关于使用Mathematica来求导可以参看已经的另一篇文章《函数求导利器——Wolfram语言》,中文源代码下载方式也在其中提供了。
本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,本人也会不断修订完善的。您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
参考资料:《微积分的历程》,维基百科,图自网络,如有不妥,请联系删除。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











