没有最伟大的数学家,就没有现代数学史。——John Forbes Nash, Jr
数学是人类智慧的结晶,在万年之后,我们再來回首与之相关的一个一个重要时刻,畅游在这时空之中,与各位大师相遇相识,惊叹数学在人类文明发展中都有些什麼让人惊叹的瞬间!
一、700年:巴比伦天文学
利用算术方法预测行星的位置
古巴比伦王国的天文学家已经能够进行详细的天文观测,其主要目的是为了占星预测。他们把自己智慧的结晶记录在了数以百计的黏土上(就是下图看上去像月饼的东西)

图1
泥板上的碑文显示,他们会测量(从地球上看到的)木星在其轨道上的不同日期的日常视速度。然后,他们会使用这些速度和时间推断木星在此期间必定将运行的距离。

图2
这种计算相当于绘制速度与时间的几何学概念,并利用绘图的结果计算面积,这种方法是现代微积分的雏形,大约在1400年后才出现在中世纪的欧洲。
二、600年:毕达哥拉斯定理
每个人都会学习到的数学定理
“直角三角形两直角边的平方和等于斜边的平方”,这又称勾股定理,在古希腊发现此定理是毕达哥拉斯,他在数学上有许多重要的贡献。虽然把此定理归功于他,不过有证据表明这一定理在毕达哥拉斯出生之前早已出现。
如早在之前五百多年,中国的数学家,商高就已经发明了“勾三股四弦五”的理论,但是一直都未公诸于世,也未被世人所採认。

图3
据说毕达哥拉斯证明了这个定理后,即斩了百头牛作庆祝(百牛大祭),因此又称百牛定理。但这个说法显然是以讹传讹,众所周知毕达哥拉斯主义者在古代以素食闻名。

图4:名画《雅典学院》中左下角(标注6)抱着书在跟孩子讲课的即为毕达哥拉斯。
三、548年:围棋
世界最古老的棋类运动之一
围棋起源于中国古代,传说尧的儿子丹朱顽劣,尧发明围棋以教育丹朱,陶冶其性情。

图5
隋代张盛墓出土的围棋盘模型,该围棋盘盘面纵横19道,共361个交叉点,表明隋朝初期或更早,19道围棋盘就已经出现并沿用至今。围棋的复杂度在于其棋盘的变化无穷,差一个子盘面就可能天翻地覆,同时状态空间大,也没有全局的结构。

图6
1997年超级计算机“深蓝”战胜了国际象棋世界冠军卡斯帕罗夫,但围棋一直被认为是人工智能要在围棋上战胜人类,还要再等100年。但仅在20年后Google DeepMind实验室的AlphaGo就已经胜过人类了。
四、540年:毕达哥拉斯学派
“万物皆数”
年轻时毕达哥拉斯在去巴比伦和埃及游历求学回来之后,就创建了政治,宗教,数学于一身的秘密学术团体——毕达哥拉斯学派。他们有很奇怪的教规,每个教徒都必须宣誓严守秘密,将一切发明归之于领袖,并终身只加入这一学派,其学派的活动也是在神秘的氛围中秘密进行。

图7
毕达哥拉斯有一个关于数字的惊人发现:音程依赖于简单的数字之比。依此结论结合深入的思考和大量的细致的观察和经验归纳得出了“万物皆数”的理论,就是说宇宙间任何关系都可以整数和整数之比来表达。
五、500年:第一次数学危机
无理数的发现
在“万物皆数”的和谐体系下,世界上只有整数和分数(有理数)。而同样是该学派的弟子希帕索斯却发现了令人震惊的“无限不循环小数”,即无理数,令该学派感到恐慌,并引发了第一次数学危机。有传言说最终希帕索斯被自己的老师毕达哥拉斯(Pythagoras)判决淹死。

图8
六、476年:算筹在中国普遍使用
“运筹如飞,人眼不能逐”——《梦溪笔谈》
算筹是中国古人发明的一种数学工具,也称作筹、算子等,一般是一些具有同样长度和粗细的小棒。

图9:台湾国立自然科学博物馆内藏的汉朝骨制算筹复制品
使用算筹进行计算的方法,则称为筹算。其实就是用现成的小木棍做计算,个位用直式,十位用横式,百位再用直式……这样纵横交替摆放,就可以摆出任意大的数字来了。
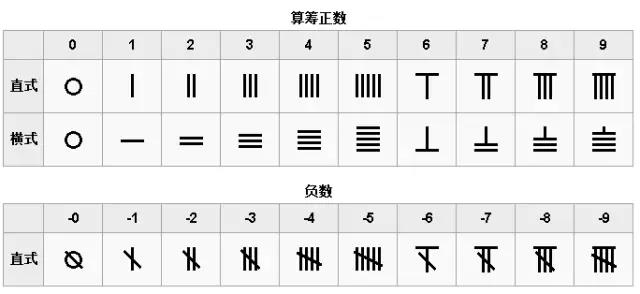
图10
中国古代数学几乎未采用任何数学符号,仅依赖筹式解决了西方数学要用许多符号才能解决的问题。这一特点使得在相当一段时期内,中国古代数学在实际应用方面位于世界前列。但是这种特点也妨碍了中国古代数学的抽象化和理论化。
七、445年:芝诺悖论
古希腊时期的诡辩术
芝诺是古希腊时代的哲学家,后人多称他为诡辩论者。他提出过众多“芝诺悖论”,其中最著名的是“飞矢不动”和“阿基利斯追不上乌龟”。
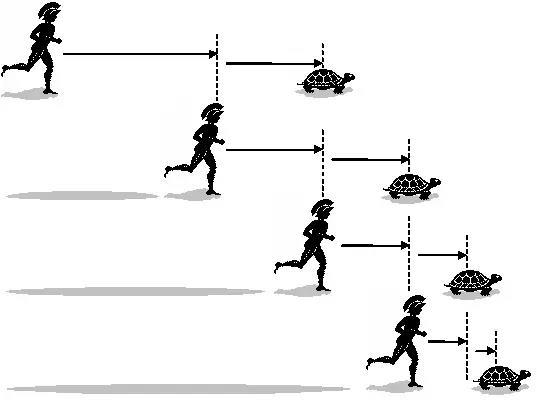
图11
传说阿基利斯奔跑速度极快,但芝诺说:如果让乌龟先跑一步,阿基利斯就永远追不上乌龟。芝诺的解释是这样的。假设乌龟先跑出了一米,阿基利斯要追上乌龟,就必须先到达半米的地方。但是,当阿基利斯到达半米的时候,乌龟与阿基利斯的距离不是半米,而是半米再加一点,比方说是0.6米。如此推论循环下去,只要乌龟不停下脚步,阿基利斯便永远只能更接近乌龟,而不能追上或超过乌龟。
八、387年:柏拉图学院
“不懂几何学者不得入match内!”
古希腊哲学家柏拉图在约前387年创立于于雅典的学校,许多古希腊哲学名士曾受教于此。例如后来开创“逍遥学派”、建立自己学校的亚里斯多德便曾在此念了20年书。

图12
在《雅典学院》这幅作品中,透视点的二人分别为柏拉图(14)及亚里士多德(15),一个以指头指着上天,另一个则伸出右指指着他前面的世界(见下大图),以此表示他们不同的哲学观点:柏拉图的唯心主义和亚里士多德的唯物主义。以他们两人为中心,两侧分别画出的其他著名学者。
九、350年:亚里士多德
引领西方世界科学论证长达两千多年
他是柏拉图的学生,亚历山大大帝的老师。亚里士多德讲课时有一个习惯,即边讲课,边漫步于走廊和花园,正是因为如此,学园的哲学被称为“逍遥的哲学”或者“漫步的哲学”,而亚里士多德的追随者也被称为逍遥学派弟子。

图13
三段论法是亚里士多德最主要的分析工具之一,只要前面两个前提为真,那么下来的结论也一定为真,譬如:“所有女人都会死亡,埃及艳后是个女人,所以埃及艳后也会死亡。”
十、325年:亚历山大图书馆
曾是世界上最大的图书馆
亚历山大图书馆由埃及托勒密王朝的国王托勒密一世所命令建造,以亚里斯多德的学园为样板,透过重金收购、雇人抄写、掠夺和兼并等管道(如,来往亚历山大港口的各地商船都被扣留下来,直到船上的所有书稿、手稿被埃及人抄下来才允许离开;复制与埃及王国交好的其他国家的书卷;派遣图书馆工作人员到远方购买成套的经典等)。亚历山大图书馆可能收集了五十万卷卷轴,涵盖了所有知识领域的作品。

图14:亚历山大图书馆想象图
后来亚历山大图书馆惨遭火灾,因而被摧毁。2000多年前它到底是什么模样无人知晓,因为它连一个石块实物也没有留下。
十一、300年:欧几里得《几何原本》
数学史上最成功的一本教科书, 现代数学的基础
《几何原本》是古希腊数学家欧几里得所著的一部数学著作,共13卷,在西方是仅次于《圣经》而流传最广的书籍。曾被翻译成阿拉伯文,然后再二手翻译成拉丁文。最先的印制本出现于1482年(见上图)。

图15
欧几里得知识渊博,数学造诣精湛,尤其擅长于几何证明。当时国王也经常向他请教数学问题,有一次国王做一道几何证明题,接连几天都没有做出来,就问欧几里得,能不能把几何证明弄得简单一点。欧几里得不客气的回答说:“陛下,几何学里没有王者之路。”这句话流传下来,成为学习几何的箴言。
十二、287年:数学之神——阿基米德
给我一个支点,我可以撬动地球
他对数学和物理学的影响极为深远,被视为古希腊最杰出的科学家。他与牛顿和高斯被西方世界评价为有史以来最伟大的三位数学家。据说阿基米德经常为了研究而废寝忘食,走进他的住处,随处可见数字和方程式,地上则是画满了各式各样的图形,墙上与桌上也无法幸免地成了他的计算板。

图16:1620年费地的布面油画《沉思的阿基米德》
国王曾让他解决打造王冠是否纯金的问题,阿基米德经过冥思苦想,在洗澡的时候发现解决的方法,使用了浮力的原理来判断黄金王冠的密度是否小于等同质量的纯金块。
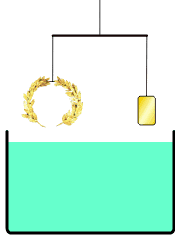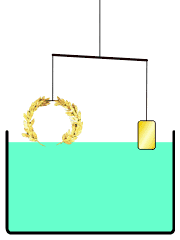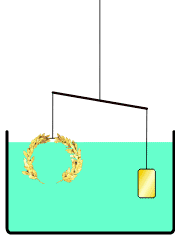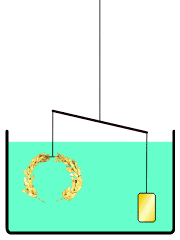
图17
公元前250年左右,阿基米德计算出π的近似值为小于3+(1/7)而大于3 + (10/71)。
十三、202年:九章算术
现存最早的中国古代数学著作之一
九章算术内容丰富,题材广泛,共九章,分为二百四十六题二百零二术,不但是汉代重要的数学著作,在中国和世界数学史上占有重要的地位。

图18
《九章算术》共收有246个数学问题,分为九大类,在一个或几个问题之后,列出这个问题的解法。
十四、200年:埃拉托斯特尼
推算出地球圆周的人
埃拉托斯特尼曾为《亚历山大图书馆》馆长,贡献在于创建经纬度系统,并使用它来绘制已知世界的地图。他就任馆长后,在古书中读到“每年6月21日(夏至)中午在尼罗河第一个瀑布赛印,垂直竖立的柱子是没有影子的”,由此思考并推测地球应该是圆的。
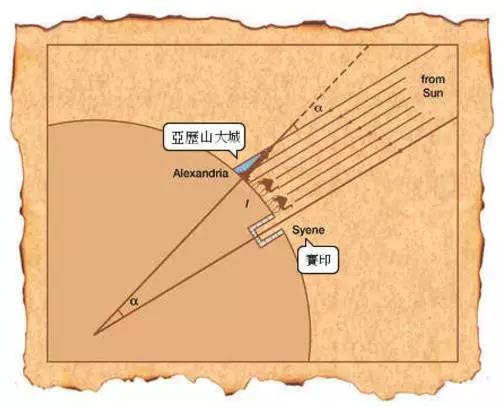
图19
他还发明出第一套寻找素数的方法——埃氏筛检法,用来找出一定范围内所有的素数。所使用的原理是从2开始,将每个素数的各个倍数,标记成合数,然后删除……迭代重复。下面是一个动画:
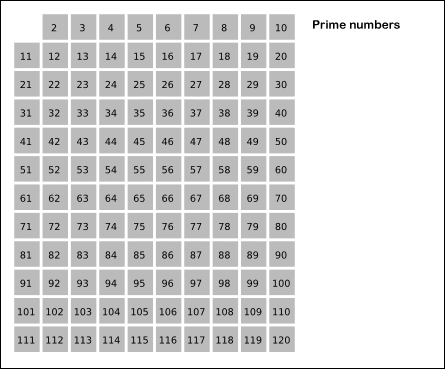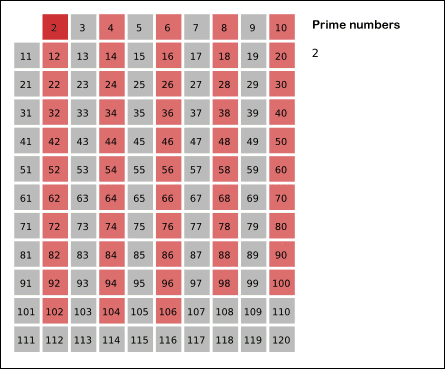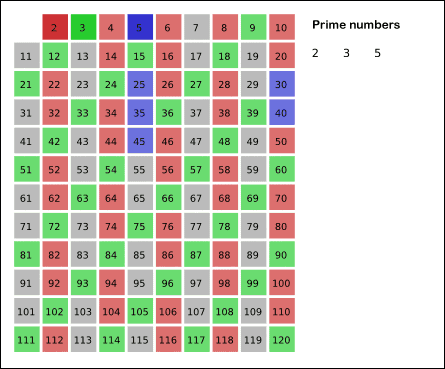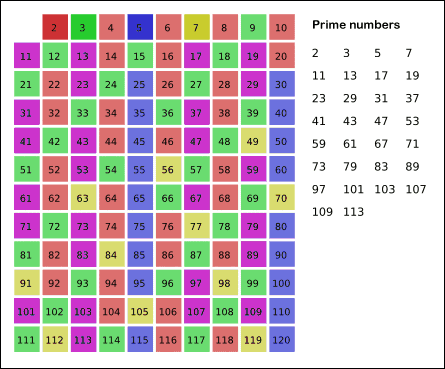
图20
十五、100年:安提基特拉机械
目前所知最古老的复杂科学计算机
安提基特拉机械是古希腊时期为了计算天体在天空中的位置而设计的青铜机器,该机器内含多个齿轮,被认为是世界上第一个模拟计算机。

图21
安提基特拉机械以其小型化和其部分装置的复杂性可与19世纪机械钟表相比而闻名。它有超过30个齿轮,虽然麦可·莱特认为它可多达72个有正三角形齿的齿轮。当借由一个曲柄(今日不存)输入一个日期,该机械就可算出日月或行星等其他天体位置。下图为重建品。

图22
本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,本人也会不断修订完善的。您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
参考资料:维基百科,百度百科,《数学之书》,《可计算知识时间轴图》。图自网络,如有不妥,请联系我删除。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











