一个数学家的目的,是要了解数学。历史上数学的进展不外两途:增加对于已知材料的了解,和推广范围。——陈省身
数学是人类智慧的结晶,在万年之后,我们再來回首与之相关的一个一个重要时刻,畅游在这时空之中,与各位大师相遇相识,惊叹数学在人类文明发展中都有些什麼让人惊叹的瞬间!
一、1045年:活字印刷术
世界上最早的活字印刷技术
毕昇在宋庆历年间发明在胶泥上刻字,一字一印,用火烧硬后,便成活字。印好后拆版,取下活字,各放入小木格内,外面按字韵分类,贴上纸标签,以便检索。

图1
不过活字印刷术在古代中国并未普及。汉字数量众多,活字印刷不及西方文字便利,对技术和要求也较高。
二、1050年:贾宪三角
贾宪三角,杨辉三角形,帕斯卡三角
宋数学家贾宪发明了贾宪三角,并发明了增乘方造表法,可以求任意高次方的展开式系数。贾宪还对贾宪三角表(古代称数字表为“立成”)的构造进行描述。

图2:《永乐大典》一页:杨辉引用贾宪《释锁算书》中的贾宪三角形
三、1088年:沈括的《梦溪笔谈》
中国科学史上的重要文献
北宋的沈括所著百科全书式的著作,因为写于润州(今镇江)梦溪园而得名,收录了沈括一生的所见所闻和见解。内容涉及天文、数学、物理、化学、生物、地质、地理、气象、医学、工程技术、文学、史事、美术及音乐等学科。

图3
书中开创了“垛积术”(高阶等差级数求和)和“会圆术”(求出弧长的方法)。
四、约1150:婆什迦罗著《天文系统极致》
印度数学的最高成就
婆什迦罗,印度古代和中世纪最伟大的数学家,天文学家。对数学主要贡献:比牛顿和莱布尼茨早五个世纪就构想了微积分;采用缩写文字和符号来表示未知数和运算;他广泛使用了无理数,并在运算时和有理数不加区别。

图4:婆什迦罗及他设计的永动机
他所著关于算数的书《Lilavati》背后有很多有趣的传奇,该书是写给他的女儿Lilavati的。其中一个故事说,婆什迦罗占星,预知了她丈夫会在婚后很快死去。为了避免这个悲剧发生,他要在一个他用一种特殊仪器测量的精确的时间地点举办婚礼。他把仪器放在一个房间,放上警示提醒Lilavati不要靠近。Lilavati好奇,往仪器里窥视,刚巧她鼻环上的一颗珍珠掉了进去,干扰了仪器。婚礼在错误的时间举行了,她很快成了寡妇。据说婆什迦罗教授了她很多数学来给她散心,并为她写成了那本书。
五、约1200年:算盘(Abacus)
影响人类文明最重要的工具之一
徐岳,东汉著名数学家,天文学家,所著《数术记遗》中第一次记载了算盘的样式,并第一次定名为“珠算”。
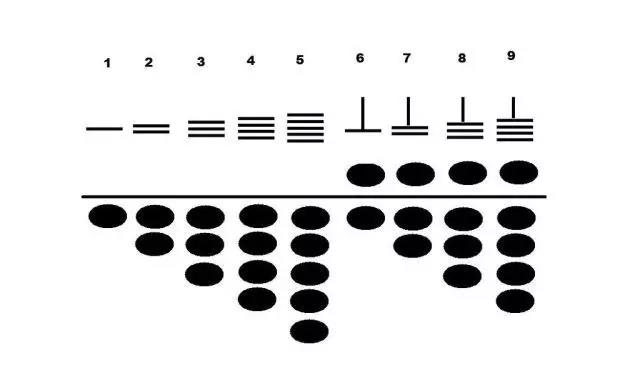
图5:算盘——算筹的化身
国际上还有一种看法,认为算盘是在公元前2400年左右在巴比伦发明的。
六、1202年:斐波那契《计算之书》
阿拉伯记数法被引入欧洲
意大利斐波那契著《计算之书》向欧洲人介绍了印度—阿拉伯记数法,整数和分数的各种算法。收集了中世纪时期用于解决日常问题的数学方法及其在商贸、度量称衡、货币换算、单利算利计算等各种场合的应用。

图6
该书再版时增加了著名的兔子繁殖问题,介绍了斐波那契数列。
七、1299年:朱世杰著《算学启蒙》
代表了宋元以来的最高水平
中国朱世杰著《算学启蒙》与《四元玉鉴》,他在当时天元术的基础上发展出“四元术”,也就是列出四元高次多项式方程,以及消元求解的方法。他吸取了各种先进的思想,并加以创造性的发展。 该书曾流传到朝鲜和日本,对世界数学的发展产生影响。
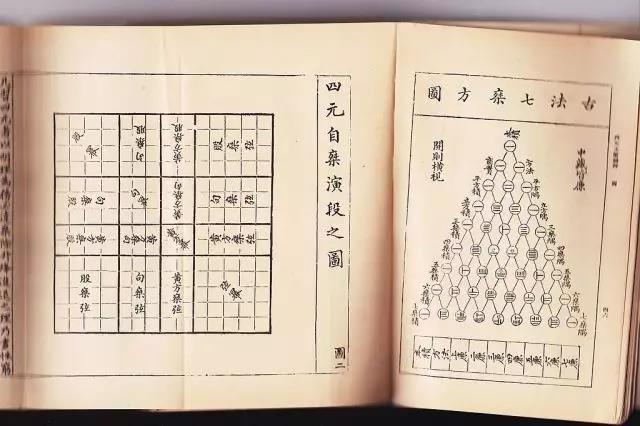
图7:四元自乘演段图
八、1408年:《永乐大典》
世界有史以来最大的百科全书
《永乐大典》是中国最大的一部类书,编撰于明永乐年间,全书22,937卷,11,095册,约3.7亿字。《永乐大典》屡遭浩劫,正本不知去向,副本今存不到800卷,约为原书的4%。

图8:明成祖朱棣全身像及所令修纂永乐大典
九、1427年:卡西著《算术之钥》
涉猎了当时几乎全部的数学知识
阿拉伯数学家阿尔·卡西(Jamshīd al-Kāshī)著《算术之钥》,涉及算数学,代数学,几何学,三角函数,数论,天文学,物理学,测量学,建筑学和法律学(遗产分配问题)等内容,被称为初等数学百科全书,对伊斯兰世界和欧洲数学影响达数百年之久。
卡西在另一本著作《圆周论》书中算出了圆周率17位有效数字,终于打破了祖冲之1千年前7位有效数字的记录。

图9:卡西画像及计算圆周率手稿
他给出了余弦定理的一种形式,所以在法国把此定理也称作阿尔·卡西定理。
十、1453年:古腾堡发明的印刷机
启动了一场前所未有的新资讯爆炸
古腾堡受中国的活字印刷启发,在德国的美因兹造出了使用合金活字的印刷机,并研製出了印刷用的印油和铸字的字模,还用活字印刷术印製《圣经》——这是欧洲第一部使用活字印刷技术的书籍,并且是截至目前的畅销书。

图10:古腾堡及当时的印刷机
印刷机的开发使知识的传播发生了革命性的变化,从欧洲开始,然后扩及全球,直到五百多年后的今天。
十一、1509年:帕西奥利著《神圣的比例》
会计学之父
意大利卢卡·帕西奥利是列奥纳多·达·芬奇的好友,其在意大利各处的教学活动和编写的教材大大影响了后来的数学教学和研究。他所著《神圣的比例》出版,主题为比例,特别是黄金分割在数学和艺术上的重要性。
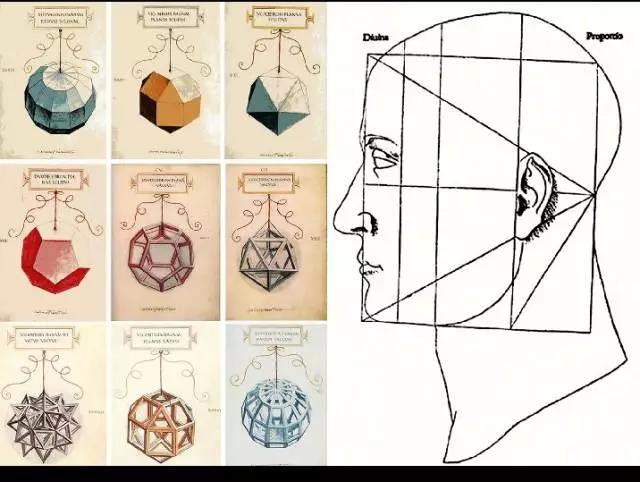
图11:部分插图及人头部黄金分割比例关系插图
他在著作中对复式记账法的记载和研究被认为是会计学的开端,故被称为“会计学之父”。
十二、1545年:卡尔达诺的《大术》
嗜赌如命的数学家
意大利数学家,也称卡当。《大术》是一部探讨代数问题的书籍,书中发表了三次代数方程一般解法的卡尔达诺公式,也称卡当公式(但真正发明此三次代数方程解法的为塔塔利亚)。书中还记载了四次代数方程的一般解法(由他的学生费拉里发现)。此外,在代数学上的另一个贡献,他还最早使用了复数的概念。

图12
除了上面的成就,在概率论也扮演了奠基人的角色,还发表了第一部概率论著作。然而对于这样一个数学家,却一个嗜赌如命的赌徒,几乎天天都呆在赌场里(难怪概率玩的转)。而且,卡当的死也与赌博相关。当时宫廷占星家他通过占星术推算出自己的忌辰,但是到那一天时,他活得还是欢蹦乱跳,为了保全自己大星象家的名声,他选择了自杀。
十三、1569年:麦卡托投影法
使得地图投影能够成为理想的导航地图
本投影法得名于杰拉杜斯·麦卡托,他于1569年发表长202公分、宽124公分以此方式绘制的世界地图。

图13
在以此投影法绘制的地图上,经纬线于任何位置皆垂直相交,使世界地图可以绘制在一个长方形上。由于可显示任两点间的正确方位,航海用途的海图、航路图大都以此方式绘制。在该投影中线型比例尺在图中任意一点周围都保持不变,从而可以保持大陆轮廓投影后的角度和形状不变(即等角)。

图14
但麦卡托投影会使面积产生变形,比如格陵兰岛看上去比实际大5倍,而极点的比例甚至达到了无穷大。
十四、1572年:虚数
不存在的数
拉斐尔·邦贝利,意大利文艺复兴时期欧洲著名的工程师,同时也是一名卓越的数学家。其出版于1572年的《代数学》一书讨论了负数的平方根(虚数)。

图15
十五、1582年:公历的建立
以地球绕行太阳一周为一年
现行公历(Gregorian calendar),又译格里历。罗马天主教会第227任教皇格列高利十三世建立了现代日历,每四年在2月底置一闰日,但格里历特别规定,除非能被400整除,所有的世纪年(能被100整除)都不设闰日;如此,每四百年,格里历仅有97个闰年。

图16:月名由来
十六、1595年:新代数学符号的诞生
16世纪法国最有影响的数学家之一
弗朗索瓦·韦达(Franciscus Vieta),著名律师,数学是他的业余爱好。他是第一个有意识地、系统地使用符号的人。他不仅用字母表示未知量和未知量的乘幂,而且用来表示一般的系数。他把符号代数称为类的算术,以别于数的算术。他还发现了代数方程根与系数的关系的韦达定理。

图17
本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,本人也会不断修订完善的。您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
参考资料:维基百科,百度百科,《数学之书》,《可计算知识时间轴图》。图自网络,如有不妥,请联系删除。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











