他以几乎神一般的思维力,最先说明了行星的运动和图像,彗星的轨道和大海的潮汐。——牛顿墓志铭
数学是人类智慧的结晶,在万年之后,我们再來回首与之相关的一个一个重要时刻,畅游在这时空之中,与各位大师相遇相识,惊叹数学在人类文明发展中都有些什麼让人惊叹的瞬间!
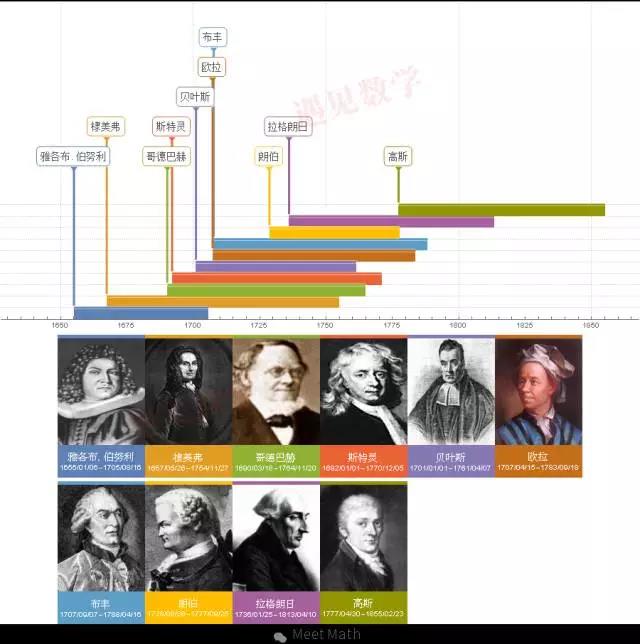
图1
一、1712年:微积分第一发明人之争
数学史最大的公案
牛顿所在的英国皇家学会于此年宣布,经过调查表明了牛顿才是微积分第一的发现者,而莱布尼茨被斥为骗子。由此激化了牛顿与莱布尼茨关于微积分发现的争论。并阻碍列欧洲和英国数学家之间相互交流,拒绝更为简便的莱布尼茨发明的符号。

图2
二、1713年:大数定律的发表
概率论早期最重要的著作之一
瑞士雅各布·伯努利出版《猜度术》,书中载有伯努利大数定律(Law of large numbers)。他发现在重复试验中,随着试验次数的增加,事件发生的频率趋于一个稳定值。
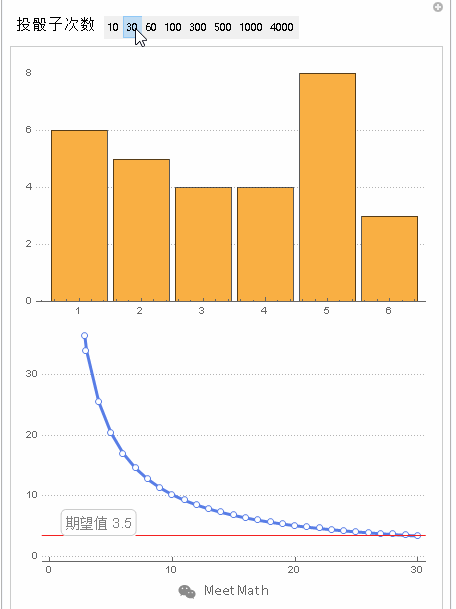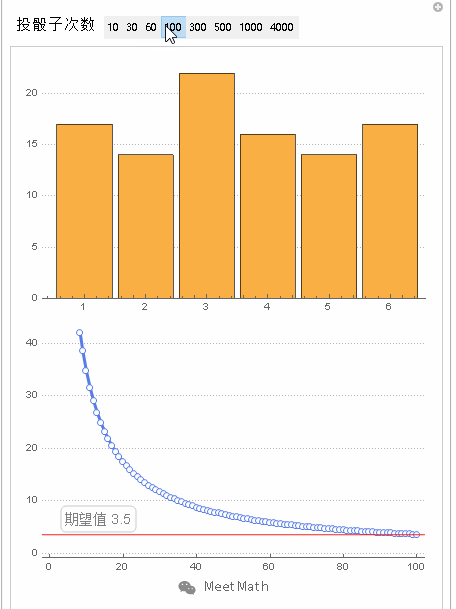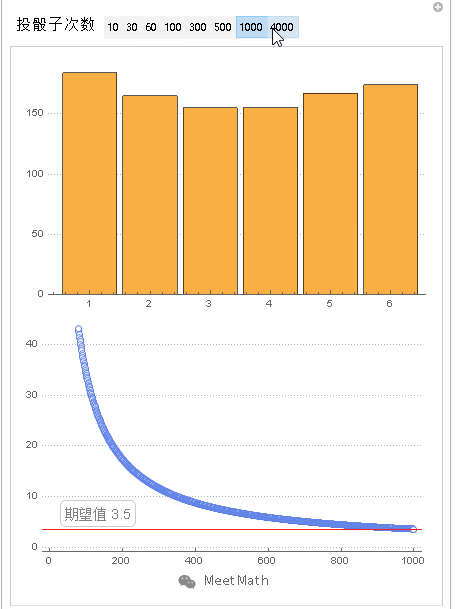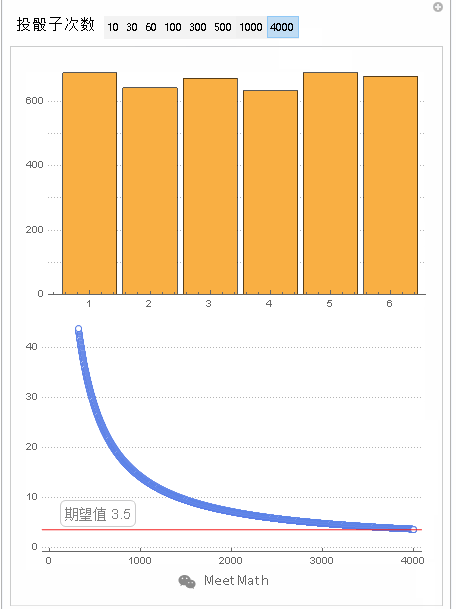
图3
以特定掷单个骰子的过程来展示大数定律。随着投掷次数的增加,所有结果的均值趋于3.5(骰子点数的期望值)。不同时候做的这个实验会在投掷数量较小的时候(左部)会表现出不同的形状,当数量变得很大(右部)的时候,它们将会非常相似。
三、1723年:《御製數理精蘊》
达到乾嘉时期数学研究的高潮
康熙在位时既倡导西算,也重视中算。由他帝主持,梅毅成等集体编写的数学百科全书《御製数理精蕴》于雍正元年(1723)十月刻竣。
《数理精蕴》是一部介绍包括西方数学知识在内的数学百科全书。全书分上下两编及附录。上编五卷专讲数理,立纲明体,是全书的基本理论部分。

图4
四、1727年:欧拉数E
关于增长率和变化率的常数
瑞士欧拉在《关于最近所做火炮发射试验的思考》中,引进记号 e 表示自然对数的底。并且欧拉1735年首次引进记号f(x)表示变量x的函数。

图5:欧拉本人及 e
瑞士数学家雅各布·伯努利在研究复利的时候发现的e,并且知道会是一个2~ 3之间的数,但最终的结果很可惜他并没有计算出来。这个问题还是由50年后的欧拉搞定。
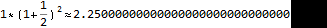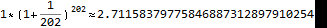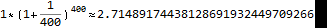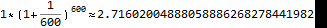
图6
五、1730年:斯特灵公式
计算阶乘精妙的计算方法
阶乘符号n!是由法国数学家克里斯蒂安·克兰普发明。一般来说,当n很大的时候,n阶乘的计算量十分大。
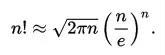
苏格兰数学家斯特灵(James Stirling)在《微分方法》中提出了斯特灵公式可以用来取n阶乘近似值。
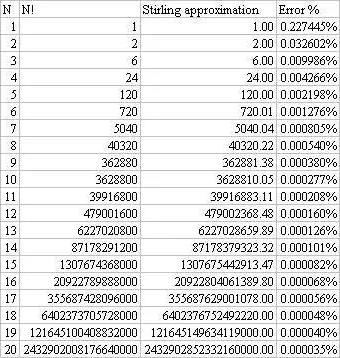
图7:阶乘与斯特灵公式的对比
六、1733年:常态分布曲线
误差理论的基石
高斯在数学上有诸多贡献,如在德国10马克上印有高斯及常态分布曲线。

图8
不过高斯倒不是第一位提出此分布者,法国数学家棣美弗(Abraham De Moivre)早于他写出此分布。
七、1742年:哥德巴赫猜想
数论中存在最久的未解问题之一
1742年6月7日,普鲁士数学家克里斯蒂安·哥德巴赫(Christian Goldbach)在写给瑞士数学家莱昂哈德·欧拉的通信中,提出了这样的猜想,用现代的数学语言,可以陈述为:“任一大于2的偶数,都可表示成两个素数之和”。
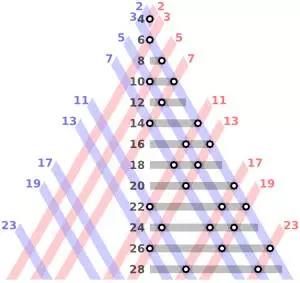
图9:将一个偶数用两个素数之和表示的方法,等于同一横线上,蓝线和红线的交点数
哥德巴赫猜想在提出后的很长一段时间内毫无进展,直到二十世纪二十年代,数学家从组合数学与解析数论两方面分别提出了解决的思路,并在其后的半个世纪里取得了一系列突破。目前最好的结果是陈景润在1973年发表的陈氏定理(也被称为“1+2”)。
八、1759年:骑士巡逻
哈密顿路径问题的一种特殊形式
骑士巡逻(英语:Knight's tour)是指在按照国际象棋中骑士的规定走法走遍整个棋盘的每一个方格,而且每个网格只能够经过一次。假若骑士能够从走回到最初位置,则称此巡逻为“封闭巡逻”,否则,称为“开巡逻”。对于8*8棋盘,一共有26,534,728,821,064种封闭巡逻,但是到底有多少种开巡逻仍然未知。

图10
欧拉在1759年开始研究它,并获得了一般解法。
九、1759年:梅毅成编成《梅氏丛书辑要》
清朝历算第一名家、数学家梅文鼎的成果
中国清代梅瑴成将祖父梅文鼎的历法、数学著述汇为《梅氏丛书辑要》,收集了其祖父的著作60卷。

图11
十、1760年:拉格朗日与变分法
变分法的建立
法国数学家约瑟夫·拉格朗日(Joseph Lagrange)发表《论确定不定积分式的极大极小值的一个新方法》是用分析方法建立变分法的代表作。发表前写信给欧拉时,称此文中的方法为“变分方法”(themethod of variation)。欧拉肯定了,并在他自己的论文中正式将此方法命名为“变分法”(the calculus of variation)。变分法这个分支才真正建立起来。

图12
十一、1761年:朗伯证明了π和e是无理数。
从理论上彻底解决了π和e的精确值问题
瑞士数学家约翰·海因里希·朗伯(Johann Heinrich Lambert)证明了π是无理数。对其他方面的数学研究有很大的启发和推动作用。

图13
十二、1761年:贝叶斯定理
平凡而又神奇的定理
英国皇家学会会员托马斯·贝叶斯(Thomas Bayes),以其在概率论领域的研究闻名于世,他提出的贝叶斯定理对于现代概率论和数理统计的发展有重要的影响。
贝叶斯定理是关于随机事件A和B的条件概率的一则定理:
图14
基于贝叶斯定理:即使100%的胰腺癌症患者都有某症状,而某人有同样的症状,绝对不代表该人有100%的概率得胰腺癌,还需要考虑先验概率,假设胰腺癌的发病率是十万分之一,而全球有同样症状的人有万分之一,则此人得胰腺癌的概率只有十分之一,90%的可能是是假阳性。
十三、1768年:大不列颠百科全书
世界上最重要的工具书之一
1768年12月6日,《大不列颠百科全书》(又称《大英百科全书》)第一版出版,尝试总结所有现有的书籍知识。

图15
2012年3月13日,不列颠百科全书宣布停止印刷版发行,全面转向电子化。
十四、1773年:命运多舛的《四库全书》
中国历史上规模最大的一套丛书
中国清代乾隆皇帝下令开设四库全书馆,清乾隆三十八年(1773年)开始编纂,历时9年成书。共收书3503种,79337卷,约8亿字。整套书收录了从先秦到清乾隆前期的众多古籍,涵盖了古代中国几乎所有学术领域,以及收入和存目了西洋传教士参与撰述的著作,包括从西洋传入中国的数学、天文、仪器及机械等方面的著作收集整理古典学术著作,纂修《四库全书》(1787年完成)。

图16
《四库全书》完成至今的两百年间,中国历经动乱,《四库全书》也同样饱经沧桑,多份抄本在战火中被毁。
十五、1777年:布丰投针问题
一个求π的蒙特·卡罗方法
法国博物学家、数学家布丰提出以下问题:设我们有一个以平行且等距木纹铺成的地板(如下图),现在随意抛一支长度比木纹之间距离小的针,求针和其中一条木纹相交的概率。这就是布丰投针问题。
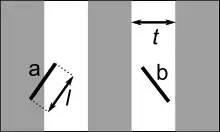
图17
十六、1794年:高斯与最小二乘法
应用最广泛的参数估计方法
最小二乘法发展于天文学和大地测量学领域,德国数学家高斯在解决行星轨道预测问题时首先提出最小二乘法。它的基本思路是选择估计量使模型(包括静态或动态的,线性或非线性的)输出与实测输出之差的平方和达到最小。这种求误差平方和的方式可以避免正负误差相抵,而且便于数学处理(例如用误差的绝对值就不便于处理)
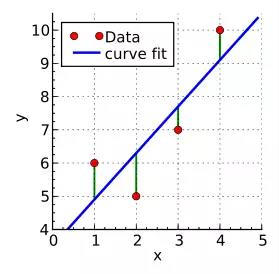
图18:数据点(红色)、使用最小二乘法求得的最佳解(蓝色)、误差(绿色)
十七、1795年:公制(Metric system)
完全创新的单位制度
公制又称米千克秒(MKS或mks)单位制,建立在下述三种基本单位之上:米——用来确定距离,千克——用来确定质量,和秒——用来确定时间长度。它根基于科学的原则,且满足日益频繁的商业活动和科学研究的需求。
其中重量的测量单位为克,即在4摄氏度是100万分之一立方米纯水的重量为一克。

图19
上是用于量度且有刻度的四个物件。卷尺划了厘米的刻度,温度计划了摄氏的刻度,砝码的质量为一千克,电表可以用伏特、安培或欧姆的电学单位进行量测。
现在全求只有3个国家不使用公制,即缅甸,利比里亚和美国。利比里亚采用了部分公制,缅甸目前正处在过渡期,只剩下美国没有使用公制。
十八、1796年:正十七边形作图
数学王子引以自豪的成果
希腊的数学已经能用圆规和无刻度直尺画出正3,4,5,15边形。但是随后的两千多年间,没有人能以直尺和圆规做出正11,13,14,17边形。1796年,高斯在 18 岁时候便解决了两千多年以来的这个几何难题,发表了《关于正十七边形作图的问题》,正十七边形其中一个作图方法如下:

图20
他以此为自豪,希望能将正十七边形刻在他的墓碑上。然而,最后刻上确实一颗十七角星。原来是负责刻纪念碑的雕刻家认为,如果是正十七边形的话,那跟圆就无法区分了。

图21
本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,本人也会不断修订完善的。您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
参考资料:维基百科,百度百科,《数学之书》,《可计算知识时间轴图》,《数学史辞典》,图自网络,如有不妥,联删。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











