“他的思想深入数学、空间、大自然的奥秘,他测量了星星的路径、地球的形状和自然力。他推动了数学的进展直到下个世纪。”——慕尼黑博物馆高斯画像题诗
法国18世纪后期到19世纪初数学界著名的三个人物:拉格朗日(Lagrange)、拉普拉斯(Laplace)和勒让德(Legendre)。因为他们三个的姓氏的第一个字母为“L”,又生活在同一时代,所以人们称他们为“三L”。
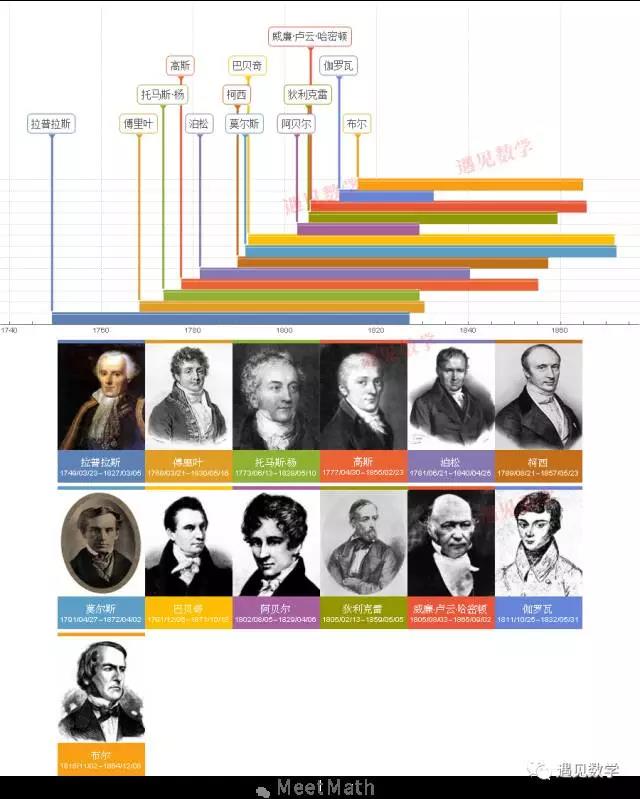
图1
一、1801年:高斯发表《算术研究》
数论领域的划时代之作
年仅 21 岁的高斯出版了《算术研究》(Disquisitiones Arithmeticae)揭开了近代数论的研究,它不仅是数论方面的划时代之作,也是数学史上不可多得的经典着作之一。书中从同余理论起步,探讨了同余齐次式,同余方程和二次剩余理论。

图2:初版的封面
关于《算术研究》,还流传着这样一个故事,1849年7月16日,哥廷根大学为高斯获得博士学位五十周年举行庆祝会。当进行到某一程序时,高斯准备用《算术研究》的一张原稿点烟,当时在场的数学家狄里克雷(后来继承了高斯的职位),像见到渎圣行为一样吃了一惊,他立刻冒失地从高斯手中抢下这一页纸,并一生珍藏它;他的编辑者在他死后从他的论文中间找到了这张原稿。
二、1802年:托马斯·杨与三原色原理
世界上最后一个什么都知道的人
托马斯·杨(Thomas Young)英国科学家,物理学家,医生,通才,是一个将科学和艺术并列研究,对生活充满热望的天才。
1802年,他提出大胆假设:所有颜色都可以通过红、绿、蓝三色的混合产生,三者比例不同,颜色就不同。三色理论为彩色电视显示系统设计奠定了理论基础。
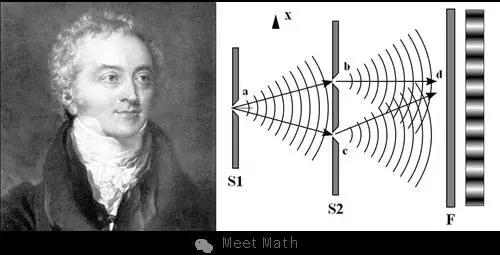
图3
杨曾进行了著名的杨氏双缝实验,证明光以波动形式存在,而不是牛顿所想象的光粒子(Corpuscles),然而,这个理论在当时并没有受到应有的重视,还被权威们讥为“荒唐”和“不合逻辑”。但杨并没有向权威低头:“尽管我仰慕牛顿的大名,但是我并不因此而认为他是万无一失的。我遗憾地看到,他也会弄错,而他的权威有时甚至可能阻碍科学的进步。”
三、1807年:傅里叶与傅里叶级数
政治上墙头草的数学大师
约瑟夫·傅里叶男爵(Joseph Fourier)法国数学家、物理学家,在热传导研究中,提出任意周期函数可以用三角级数(傅立叶级数)表示,并将其应用于热传导理论与振动理论。
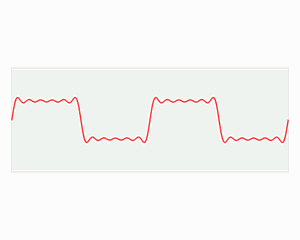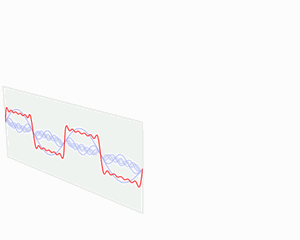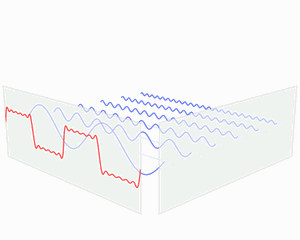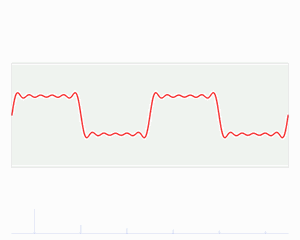
图4:函数s(x)(红色)是六个不同幅度的谐波关系的正弦函数的和。它们的和叫做傅里叶级数。傅里叶变换S(f)(蓝色),针对幅度与频率进行描绘,显示出6种频率和它们的幅度。
四、1812年:拉普拉斯《概率分析论》
被誉为法国的牛顿
皮埃尔—西蒙·拉普拉斯(Pierre-Simon Laplace)法国天文学家,数学家,1812年出版800多页《概率的分析理论》,代表了当时概率论研究的最高成就。本书集古典概率论之大成,将分析工具引入概率论,代替了早期的初等组合方法,开创了分析概率论的新阶段。

图5
拉普拉斯在天体力学的最重要成就是五卷巨著《天体力学》,后凭此书当选法兰西学院院士,成为四十位“不朽者”(Immortels)之一。
五、1823年:柯西《无穷小分析教程概论》
“不要让几何直观, 蒙蔽了我们的双眼。”
奥古斯丁·路易·柯西(Augustin-Louis Cauchy),法国数学家。于1823年出版《无穷小分析教程概论》,把定积分定义为和的极限,还给出现在通用的广义积分的定义,引进柯西积分主值的概念。

图6:柯西纪念邮票及邮戳
柯西在微积分历史上影响颇深,他认为全部微积分应当建立在极限思想的基础上:“当属于一个变量的相继的值无限地趋近某个固定值时,如果最终同固定值之差可以随意地小,那么这个固定值就称为所有这些值的极限。”
六、1824年:阿贝尔—鲁菲尼定理
19世纪最伟大的数学家之一
阿贝尔—鲁菲尼定理是代数学中的重要定理。它指出,五次及更高次的多项式方程没有一般的求根公式。 这个定理以保罗·鲁菲尼和尼尔斯·阿贝尔命名。前者在1799年给出了一个不完整的证明,后者在1824年,年仅19岁的挪威数学家阿贝尔(Niels Henrik Abel)发表论文《高于四次的一般方程的代数求解之不可能性的证明》,证明了一般五次方程不可能用根式求解,从而解决了困扰数学长达300多年之久的难题。
法国数学家夏尔·埃尔米特称赞他“丰富的数学思想可以使数学家们忙上五百年”。

图7:纪念阿贝尔的钞票及邮票
尽管阿贝尔成就极高,却生前不得志,最后因过度贫穷染上肺结核逝世于挪威的弗鲁兰。跟同样早逝的伽罗华一同被奉为群论的先驱。
2001年,为了纪念2002年挪威著名数学家尼尔斯·亨利克·阿贝尔二百周年诞辰,挪威政府设立阿贝尔奖(bel Prize)数学国际奖项,每年颁发一次,获誉为数学界最高荣誉之一。
七、1830年:查尔斯·巴贝奇与分析机
现代计算机真正的鼻祖
巴贝奇(Charles Babbage)英国维多利亚时代最杰出的人物之一,在他设计差分机的基础之上设想出一种分析机(Analytical Engine),可以运行包含“条件”、“循环”语句的程序,有寄存器用来存储数据,不过与差分机同样没有完成。

图8:巴贝奇,分析机,差分机1号、2号
1822~1832十年,巴贝奇展示出差分机一号1/7部分,差分机运转的精密程度仍令当时的人们叹为观止,至今依然是人类踏进科技的一个重大起步。差分机后因失去了政府的资助而终止。
八、1832年:伽瓦罗与群论
数学史上最富有传奇色彩的天才数学家
埃瓦里斯特·伽罗瓦(Évariste Galois)法国数学家,在他还只有十几岁的时候,他就发现了n次多项式可以用根式解的充要条件,他是第一个使用群这一个数学术语来表示一组置换的人,确立了群论的基本概念。与尼尔斯·阿贝尔并称为现代群论的创始人。

图9:伽瓦罗纪念邮票及手稿
伽罗瓦是一个激进的共和主义者,并因此被逮捕、坐牢。二十岁出狱后,因与一位舞女的恋情惹怒了当时的著名神枪手,此神枪手对他发出决斗,时间在三天后。自知必死的伽罗瓦在决斗前三夜将他的所有数学成果狂笔疾书纪录下来,并时不时在一旁写下“我没有时间”,三天后,他在决斗中中弹,几天后身亡,时间是1832年5月31日。
九、1834年:鸽笼原理
组合数学中的一个重要原理
鸽巢原理,又名狄利克雷抽屉原理。由德国数学家狄利克雷提出来的。其中一种简单的表述法为:若有n个笼子和n+1只鸽子,所有的鸽子都被关在鸽笼里,那么至少有一个笼子有至少2只鸽子。
集合论的表述如下:若A是n+1元集,B是n元集,则不存在从A到B的单射。

图10:10只鸽子放进9个鸽笼,那么一定有一个鸽笼放进了至少两只鸽子。
但有时使用鸽巢原理会得到一些有趣的结论:比如:北京至少有两个人头发数一样多。
证明:假定没有人有超过100万根头发,但北京人口大于100万。如果我们让每一个鸽巢对应一个头发数字,鸽子对应于人,那就变成了有大于100万只鸽子要进到至多100万个巢中。所以,可以得到“北京至少有两个人头发数一样多”的结论。
十、1837年:泊松与泊松分布
“人生只有两样美好的事情:发现数学和教数学。”
西莫恩·德尼·泊松男爵(Siméon Denis Poisson),是法国数学家,物理学家。在1837年发表《关于判断的概率之研究》,提出描述随机变量的泊松分布。
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数等等。
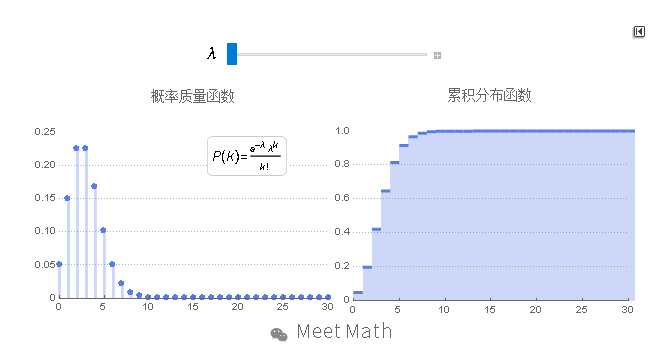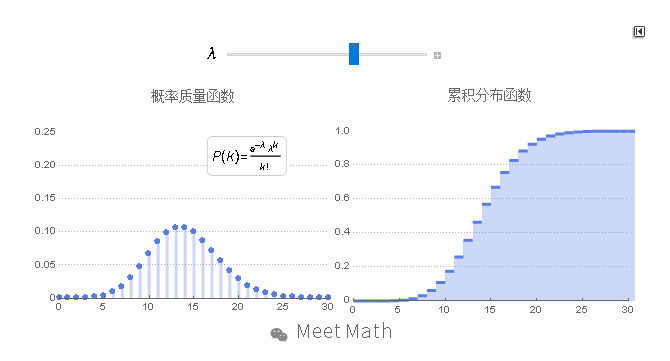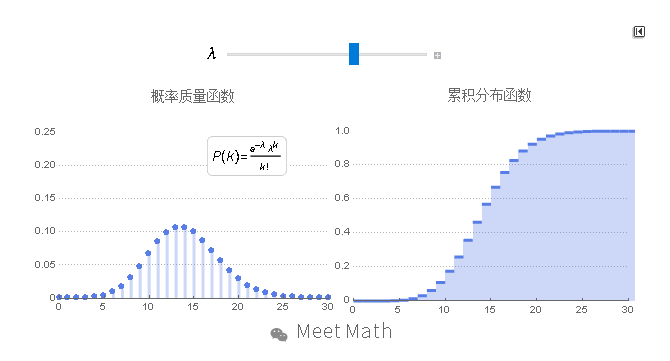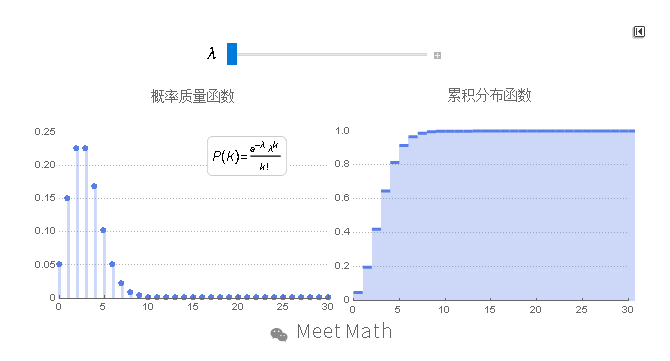
图11:横轴是索引k,发生次数。该函数只定义在k为整数的时候。
十一、1843年:四元数(Quaternion)
开启了对非对称的乘法结构的系统研究
四元数是由爱尔兰数学家威廉·卢云·哈密顿(William Rowan Hamilton)在1843年创立出的数学概念。自此用来描述在三位空间物体旋转变换的工具,它与常用的另外两种表示方式(三维正交矩阵和欧拉角)是等价的,但是避免了欧拉角表示法中的万向锁问题。比起三维正交矩阵表示,四元数表示能够更方便地给出旋转的转轴与旋转角。
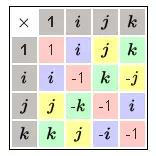
图12
十二、1844年:塞缪尔·莫尔斯与电报
“上帝创造了何等奇迹!”
塞缪尔·莫尔斯(Samuel Morse) 美国发明家,摩尔斯电码的创立者。1844年5月24日,他坐在华盛顿国会大厦联邦最高法院会议厅中,向40英里以外的巴尔的摩城发出了历史上第一份长途电报:“上帝创造了何等奇迹!”

图13:描述当时场景的画面
电报的发明,开始了用电作为信息载体的时代,成为人类通信历史上的一次巨大的飞跃。
十三、1847年:布尔发表《逻辑的数学分析》
数理逻辑奠基者
乔治·布尔(George Boole),英格兰数学家和哲学家,数理逻辑学先驱。1847年,他在《逻辑的数学分析》书中展示了如何用代数来表示逻辑。
布尔用数学语言正式地描述了逻辑学理论。之后这些理论又不断被修正,更加简单的形式逐渐被发现。1999年,Stephen Wolfram提出,其实只需要一条公理就够了。

图14:布尔代数抽象公理系统演化
真正让“布尔(Bool)”这个名字如此广为人知的不是布尔代数,而是布尔变量。基本上每一种编程语言都有布尔类型,使得“boolean”一词广为流传。
本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,本人也会不断修订完善的。您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
参考资料:维基百科,百度百科,《数学之书》,《可计算知识时间轴图》,《数学史辞典》,图自网络,如有不妥,联删。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











