一个没有几分诗人才能的数学家决不会成为一个完全的数学家。——魏尔斯特拉斯
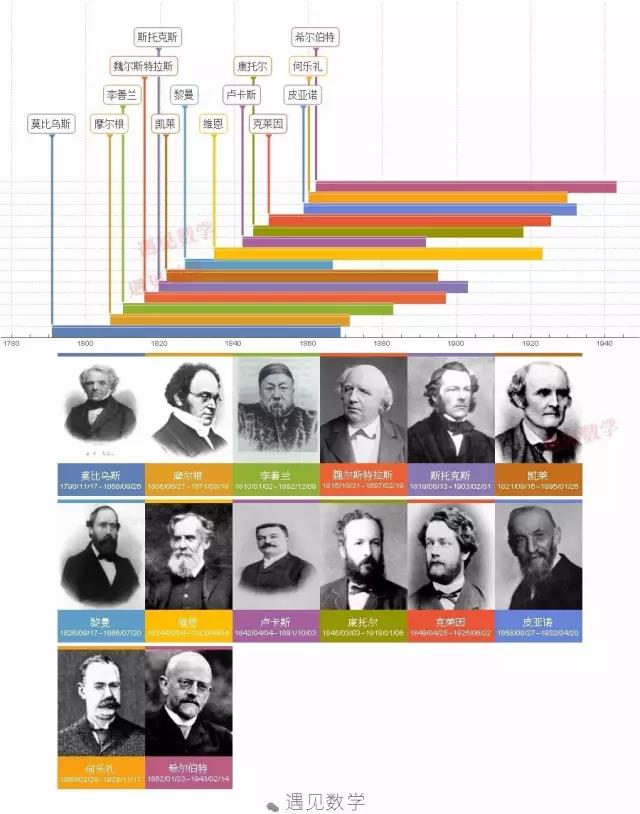
图1
一、1852年:四色定理
世界近代三大数学难题之一
1852年英国的制图员法兰西斯·古德里在绘制英格兰地图时候提出四色问题:“是否只用四种颜色就能为所有地图染色”。
图2
古德里和他弟弟在求解无果之后,他们向著名数学家德·摩尔根(Augustus De Morgan)请教,由摩尔根推动该四色问题才得到数学界的关注。
二、1854年:斯托克斯定理
揭示了的旋度和环量的关系
乔治·斯托克斯(Sir George Stokes)爱尔兰数学家,物理学家,进一步推广了格林公式,建立著名的斯托克斯定理。该定理将“向量场的旋度的曲面积分”跟“向量场在曲面边界上的线积分”之间建立联系。

图3:乔治·加布里埃尔·斯托克斯爵士
三、1858年:凯莱与矩阵理论的奠基
矩阵理论的诞生
凯莱(Arthur Cayley)英国数学家,发表《矩阵理论的研究报告》,他引入了西尔维斯特创造的"matrix"概念,定义矩阵的基本概念,矩阵的运算法则,转置,零矩阵,单位矩阵以及逆等一系列基本概念,指出了加法的可交换性和可结合性,还给出了特征方程和特征根等结果。

图4:凯莱
四、1858年:莫比乌斯带
只有一个面的魔环
奥古斯特·费迪南德·莫比乌斯(August F. Möbius)德国数学家和天文学家,拓扑学的先驱。最著名的成就是发现了三维欧几里得空间中的一种奇特的二维单面环状结构——后人称为莫比乌斯带。
莫比乌斯环的制作非常简单:将长纸条的一端扭转 180 度后,再将两端黏在一起就成了。这个结构看似简单的纸环,却有着许多奇妙的性质。一般的纸张都有正面与背面,但莫比乌斯环却只有一面。

图5:莫比乌斯及莫比乌斯带
五、1859年:黎曼猜想
当今数学界最重要的数学难题
德国数学家波恩哈德·黎曼(Bernhard Riemann)于1859年提出L
ζ(s)= 1 + 1 / 2^S+ 1 / 3^S+ 1 / 4^S+……被称为黎曼Zeta函数,黎曼猜想认为所有素数都可以表示为一个函数。
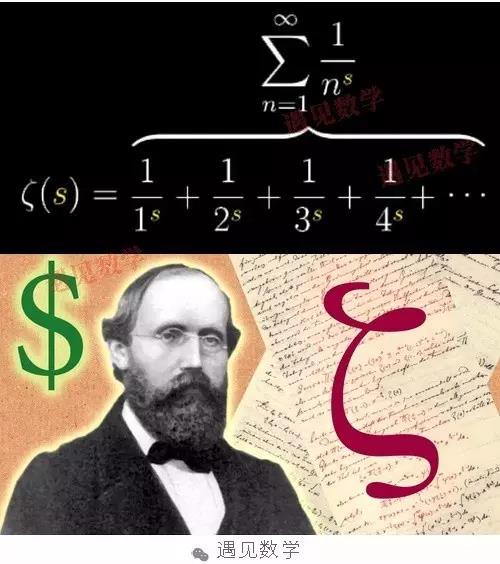
图6:黎曼及黎曼Zeta函数
六、1859年:李善兰
改变近代中国的数学家
李善兰,中国清朝数学家。李善兰恒等式为组合数学中的一个恒等式,由中国清代数学家李善兰于1859年在《垛积比类》一书中首次提出,因此得名。同年刊行了三部和牛顿物理学关系密切的译著:一是和伟烈亚力合译的《谈天》;二是和艾约瑟合译的《重学》;三是和伟烈亚力合译的《代微积拾级》。这是中国翻译西方近代数学著作的开始。

图7:李善兰(恒等式)及伟烈亚力
七、1868年:黎曼与爆米花函数
黎曼积分理论的建立
黎曼为获得格丁根大学的讲师资格,按规定提交了论文《关于用三角级数表示函数的可能性》,文中给出一组充分条件,凡满足这组条件的函数,都能展成其傅里叶级数;给出了一个连续而不可微的著名反例,最终阐明了连续性与可微性之间的关系。

图8:黎曼函数(爆米花函数)R上的所有无理点处处连续,有理点处处不连续
八、1872年:魏尔斯特拉斯
最后消除微积分不精确性的最大功臣
卡尔·魏尔斯特拉斯(Karl Weierstrass)德国数学家,被誉为“现代分析之父”。他进一步的严格化,给函数的极限建立了教科书中一直沿用到今天严格的ε-δ定义,来代替柯西的“无限趋近”描述,使极限理论成为了微积分的坚定基础,系统建立了实分析和复分析的基础。并他与1872年给出里处处连续,但处处不可微的魏尔斯特拉斯函数,推翻了当时数学家认为“连续函数绝大多数点可导”的论点。
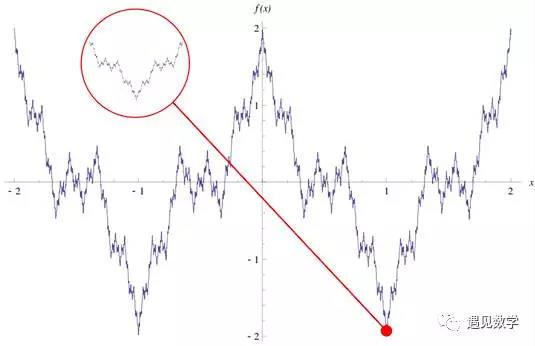
图9:区间[−2, 2]上的魏尔斯特拉斯函数。这个函数具有分形特性:某些部分会和整体自相似
九、1874年:康托尔与超限数
数学史上最富有想象力和最有争议的人物之一
格奥尔格·康托尔(Georg Cantor)发表关于超穷集合论的第一篇论文《关于一切实代数数的一个性质》,开创集合论的研究,奠定里现代集合论的基础。

图10:康托尔及对角论证法
十、1880年:约翰·维恩与文氏图
可以为事物群组分类所用的图形
约翰·维恩(John Venn)英国数学家,逻辑学家,在发表的论文中介绍了自创的集合归类方法文氏图,可以用于展示在不同的事物群组(集合)之间的数学或逻辑联系,尤其适合用来表示集合(或)类之间的“大致关系”。

图11:Google为维恩180周年诞辰设计的Doodle
十一、1882年:克莱因瓶
拓扑学中最有趣的问题之一
菲利克斯·克莱因(Felix Klein)德国数学家,提出克莱因瓶的概念。克莱因瓶是一个非常特殊的瓶子,它跟我们一般用来装水的瓶子不同:“克莱因瓶并没有边界”。
要想像克莱因瓶的结构,可先试想一个底部镂空的红酒瓶。现在延长其颈部,向外扭曲后伸进瓶子的内部,再与底部的洞相连接。
有意思的是一只苍蝇可以从瓶子的内部直接飞到外部而不用穿过表面(所以说它没有内外部之分)。
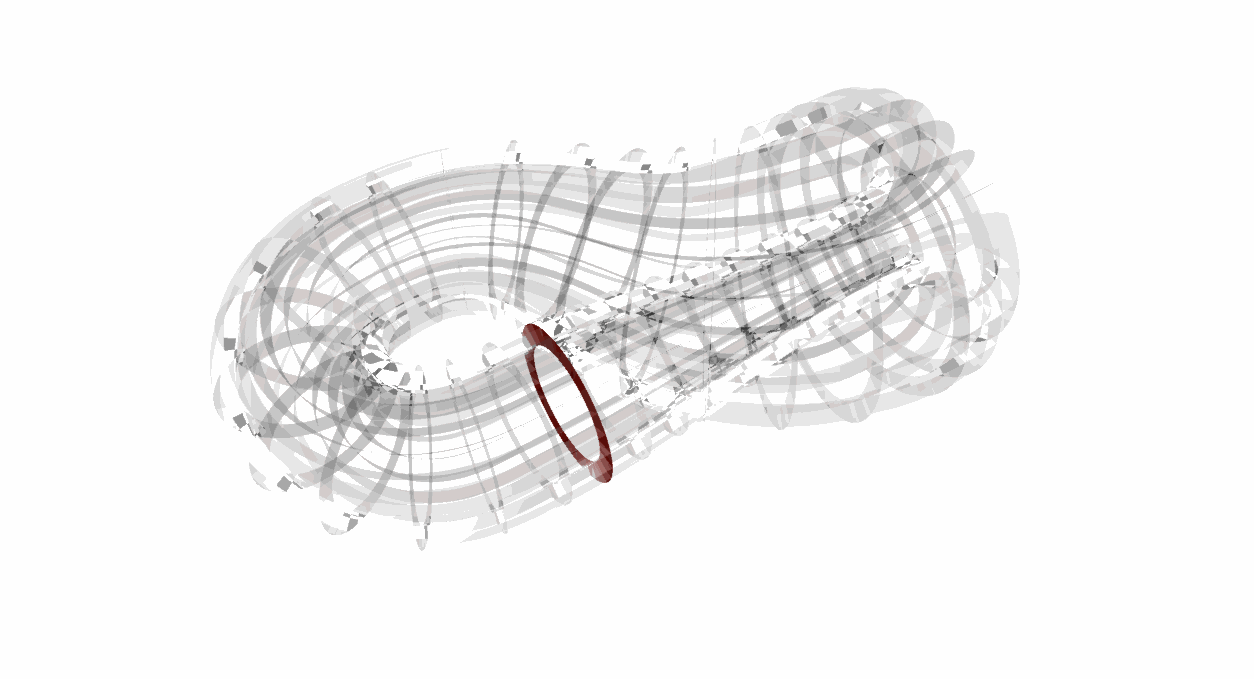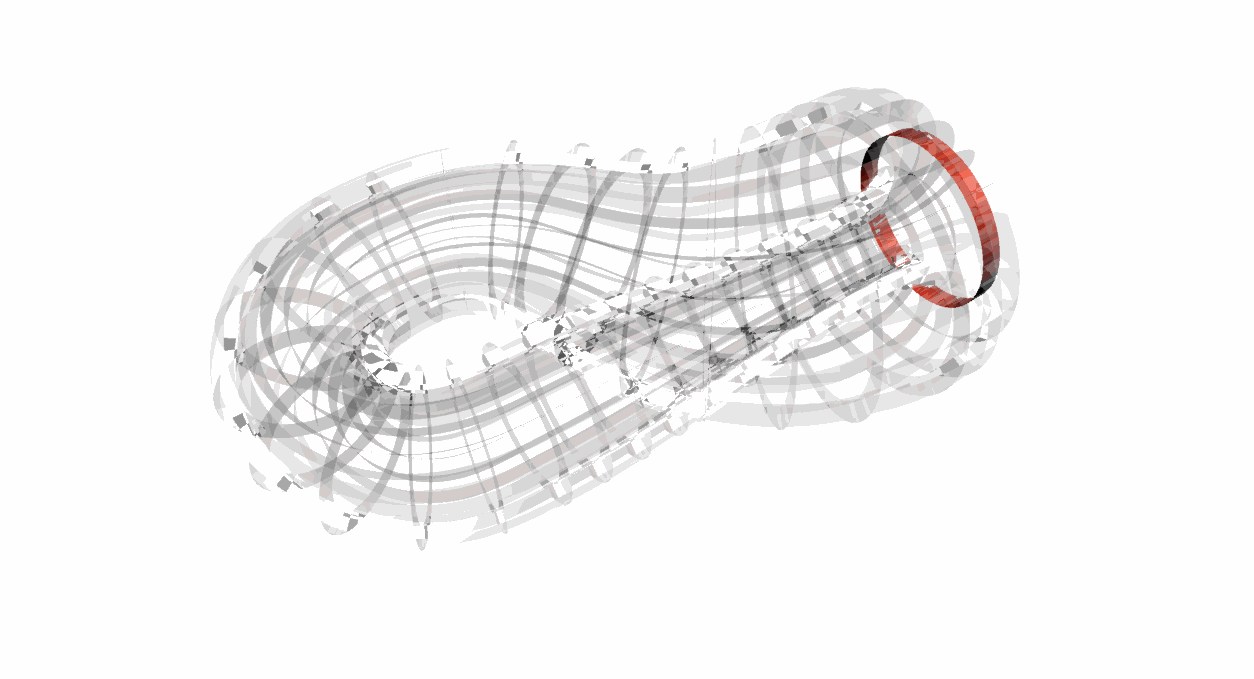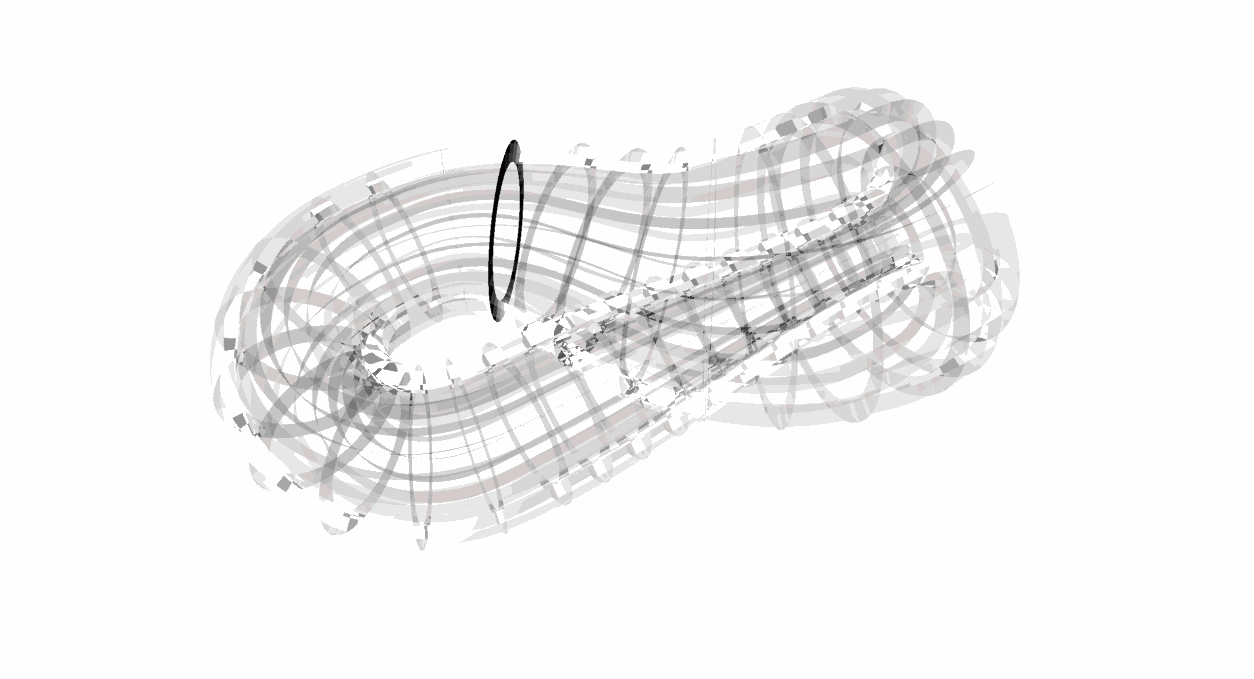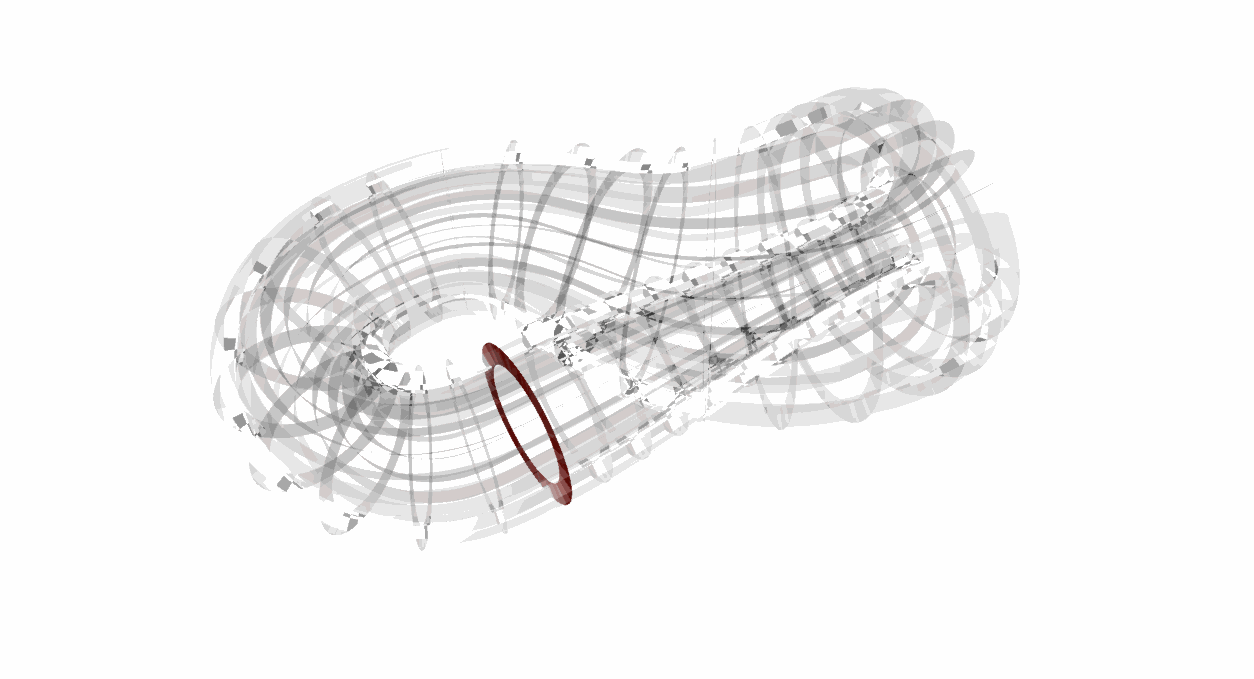
图12:克莱因瓶
克莱因认为中学教师应该多接触高等数学,以保证培养出来的学生的知识面不会出现断层;并认为当时出现的中学教师不关心高等数学发展的风气并不可取。为中学教师普及高等数学的思想就是他创作《高观点下的初等数学》的初衷。
十二、1883年:汉诺塔
递归算法的最经典示例
爱德华·卢卡斯(Édouard Lucas)法国数学家发明的一种益智游戏。有三根杆子A,B,C。A杆上有N个(N>1)穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆:
1 每次只能移动一个圆盘;
2 大盘不能叠在小盘上面。
提示:可将圆盘临时置于B杆,也可将从A杆移出的圆盘重新移回A杆,但都必须遵循上述两条规则。

图13:常见玩具版汉诺塔有8个圆盘

图14:4个圆盘的汉诺塔的移动
十三、1889年:皮亚诺公理
通过逻辑公理化知识
朱塞佩·皮亚诺(Giuseppe Peano)意大利数学家,逻辑学家,他创建了一种正式的系统和语言,其中可以通过扩展形式的逻辑来看待数学和其他知识。于1889年发表算术原理新方法提出自然数的五条公理,建立了自然数的理论。

图15:自然数的五条公理(皮亚诺公理)
次年,皮亚诺发明了能填满一个正方形的曲线,叫做皮亚诺曲线。一般来说,一维的东西是不可能填满2维的方格的,但是皮亚诺曲线恰恰给出了反例。
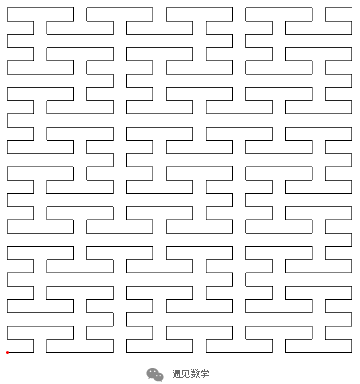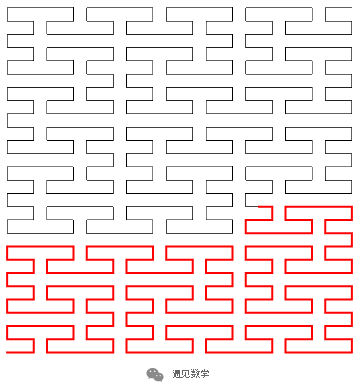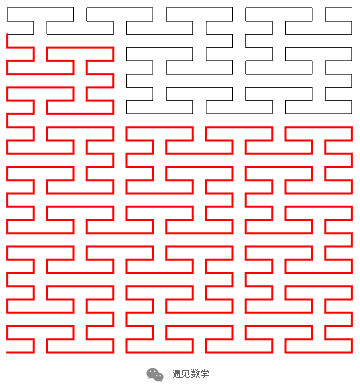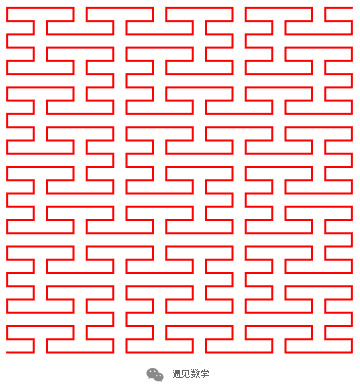
图16:皮亚诺曲线的三次迭代后遍历
十四、1890年:赫尔曼与制表机
自动数据处理的时代开启
赫尔曼·何乐礼(Herman Hollerith)德裔美籍的统计学家和发明家,基于打孔卡技术,他发明了打孔卡片制表机(Tabulation Machine)。他也是制表机器公司(Tabulating Machine Company)的创办者,该公司是IBM的前身之一。1890年,美国人口调查局将人口普查中的所有数据都放到他发明穿孔卡上,用打孔卡自动进行人口普查,仅用一年完成了上一次花费8年的工作。

图17:何乐礼和发明的打孔卡及制表机
十五、1899年:希尔伯特《几何基础》出版
20世纪数学的公理化开辟了道路
大卫·希尔伯特(David Hilbert)德国数学家,是19世纪和20世纪初最具影响力的数学家之一。于1899年出版《几何基础》,以严格的公理化方法重新阐述了欧几里得几何学,第一次给出了完备的欧几里得几何公理系统,在数学史上具有划时代意义。

图18:希尔伯特本人
希尔伯特也提出过一种能填充满一个平面正方形的希尔伯特曲线(空间填充曲线)。

图19:希尔伯特曲线经过9次迭代
本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,本人也会不断修订完善的。您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
参考资料:维基百科,百度百科,《数学之书》,《可计算知识时间轴图》,《数学史辞典》,图自网络,如有不妥,联删。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











