只要一门科学分支能提出大量的问题,它就充满着生命力,而问题缺乏则预示着独立发展的衰亡和终止。——戴维·希尔伯特
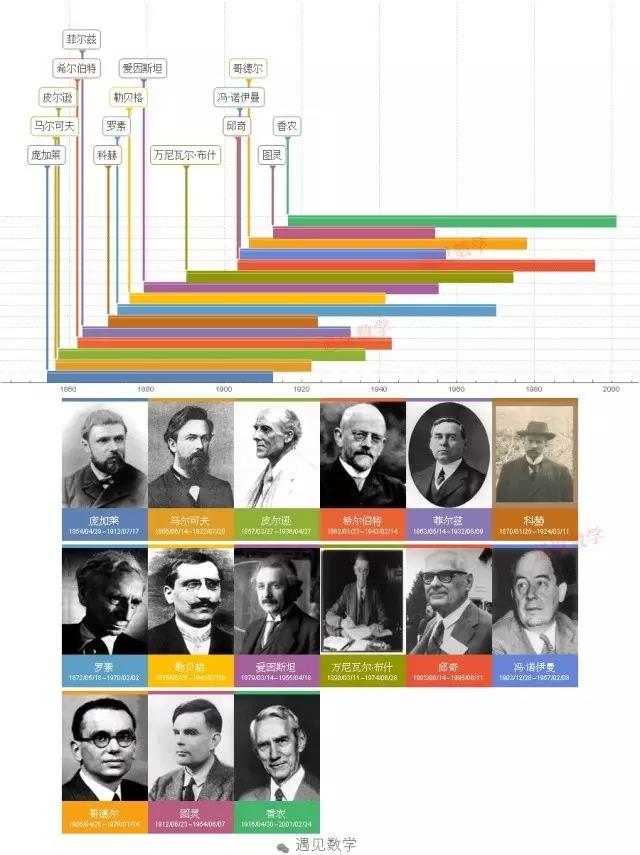
图1
一、1900年:希尔伯特的23个问题
“我们必须知道,我们终将知道。”
德国数学家希尔伯特(David Hilbert)在巴黎第二届国际数学家大会上作题为《数学问题》的报告,提出了23个著名的数学问题。
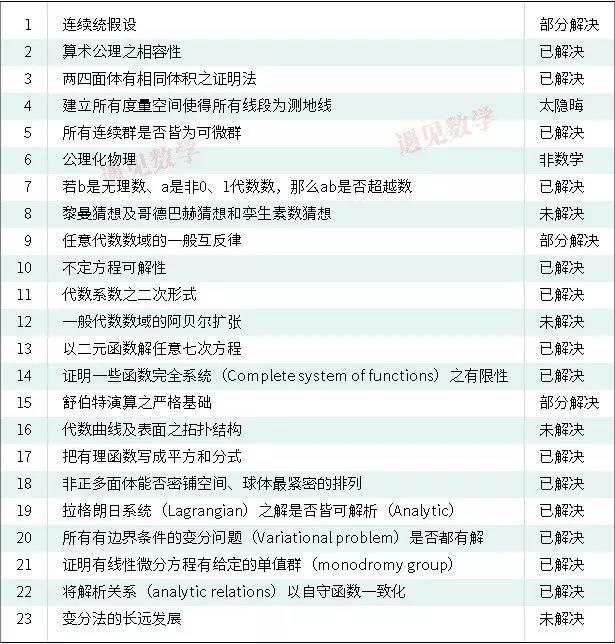
图2
据说希尔伯特退休后被人问起:“假如你去世后有一天能复活, 那么你会做什么呢?" 希尔伯特毫不犹豫地回答:"我会首先去打听黎曼猜想解决了没有。”
二、1900年:皮尔逊与卡方检定
二十世纪初统计革命的引领者之一,对生物统计研究的第一人
卡尔·皮尔逊(Karl pearson)英国数学家,他发展了回归与相关的理论,得到母体的概念,并认为统计研究不是样本本身,而是根据样本对母体的推断。由此导出了拟合优度检验:即作为样本取出的若干个体是否拟合从理论上所确定的母体分布问题。

图3:卡尔·皮尔逊
1900年,他创立和发展了卡方检定的理论,在理论分布完全给定的情况下,给出了拟合优度检验的卡方统计量的极限定理。
三、1901年:罗素与理发师悖论
第三次数学危机——集合论中的自相矛盾
理发师悖论是伯特兰·罗素(Bertrand Russell,英国数学家和逻辑学家)由在1901年提出,用来比喻罗素悖论的一个通俗说法。
小城里的理发师放出豪言:他只为,而且一定要为,城里所有不为自己刮胡子的人刮胡子。
但问题是:理发师该为自己刮胡子吗?如果他为自己刮胡子,那么按照他的豪言“只为城里所有不为自己刮胡子的人刮胡子”他不应该为自己刮胡子;但如果他不为自己刮胡子,同样按照他的豪言“一定要为城里所有不为自己刮胡子的人刮胡子”他又应该为自己刮胡子。

图4:伯特兰·罗素
四、1902年:勒贝格积分
开创现代积分理论
昂利·勒贝格(Henri Lebesgue)法国数学家,1902年发表论文《积分、长度与面积》,建立了“勒贝格测度”和“勒贝格积分”的概念。

图5:昂利·勒贝格
直观地解释与黎曼积分的原理,可以假设我们要计算一座山在海平面以上的体积。
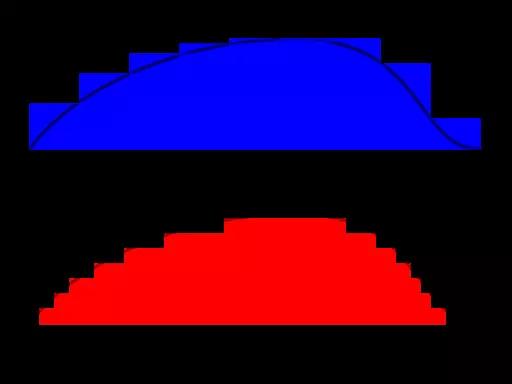
图6:黎曼积分(蓝色)和勒贝格积分(红色)
黎曼积分是相当于把山分为每块都是一平方米大的方块,测量每个方块正中的山的高度。每个方块的体积约为1x1x高度,因此山的总体积为所有高度的和。
勒贝格积分则是为山画一张等高线图,每根等高线之间的高度差为一米。每根等高线内含有的岩石土壤的体积约等于该等高线圈起来的面积乘以其厚度。因此总体积等于所有等高线内面积的和。
五、1904年:庞加莱与庞加莱猜想
历史上最后一位数学全才
昂利·庞加莱(Henri Poincaré)是法国最伟大的数学家之一。他于1904年提出猜想:“任一单连通的、封闭的三维流形与三维球面同胚。”
粗浅的比喻即为:如果我们伸缩围绕一个柳橙表面的橡皮筋,那么我们可以既不扯断它,也不让它离开表面,使它慢慢移动收缩为一个点。

图7:柳橙表面的橡皮筋
另一方面,如果我们想象同样的橡皮筋以适当的方向被伸缩在一个甜甜圈表面上,那么不扯断橡皮筋或者甜甜圈,是没有办法把它不离开表面而又收缩到一点的。我们说,柳橙表面是“单连通的”,而甜甜圈表面则不是。

图8
作为对比,图中环面上两个上色的圆均无法连续地收紧成一点,因此环面并不与球面同胚。
六、1904年:科赫曲线
最早被描述出来的分形曲线之一
海里格·冯·科赫(Helge von Koch)瑞典数学家,在其论文《关于一条连续而无切线,可由初等几何构作的曲线》提出科赫曲线。
给定线段AB,科赫曲线可以由以下步骤生成:
1 将线段分成三等份(AC,CD,DB);
2 以CD为底,向外(内外随意)画一个等边三角形DMC;
3 将线段CD移去;
4 分别对AC,CM,MD,DB重复1~3。

图9:科赫曲线的若干迭代
科赫雪花是以等边三角形三边生成的科赫曲线组成的。神奇之处在于无限长的曲线围住一块有限的面积。

图10:科赫雪花生成过程
七、1905年:质能等价公式E = mc^2
《奇迹年论文》的文章之一
阿尔伯特·爱因斯坦(Albert Einstein)20世纪犹太裔理论物理学家,创立了现代物理学的两大支柱之一的相对论。
1905年在《物理年鉴》发表了四篇划时代的论文,在《物体的惯性同它所含的能量有关吗?》中表述了质能等价公式,该式是一种阐述能量(E)与质量(m)间相互关系的理论物理学公式。

图11:质能等价公式
八、1907年:马尔科夫链
解释复杂时间进程的数学工具
俄国数学家安德烈·马尔可夫(Andrey Markov)开创了随机过程这个新的领域,以他的名字命名的马尔可夫链在现代工程、自然科学和社会科学各个领域都有很广泛的应用。
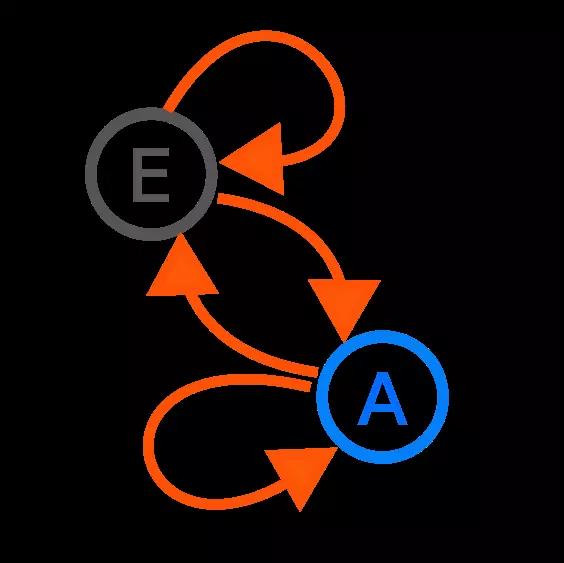
图12:一个具有两个转换状态的马尔可夫链
九、1910年:《数学原理》
推动当代数学逻辑发展与普及化
该书是由伯特兰·罗素与他的老师阿尔弗雷德·诺思·怀特黑德合著的一本数学书籍,书籍共分三卷,分别出版于1910年,1912年,1913年。企图表述所有数学真理在一组数理逻辑内的公理和推理规则下,原则上都是可以证明的。然而在1931年,哥德尔不完备性定理(库尔特·哥德尔,Kurt Gödel 奥匈帝国数学家逻辑学家)证明证明对于数学原理或其他任何类似的尝试,这个崇高的目标皆永远无法达到。

图13:数学原理
十、1925年:希尔伯特旅馆悖论
无穷带来与我们直觉相悖的思考
希尔伯特旅馆悖论是一个与无限集合有关的数学悖论,由德国数学家大卫·希尔伯特提出。
假设有一个拥有可数无限多个房间的旅馆,且所有的房间均已客满。或许有人会认为此时这一旅馆将无法再接纳新的客人(如同有限个房间的情况),但事实上并非如此。

图14
在有无限个房间时,“每个房间都客满”与“无法入住新的客人”两者其实并不等价。可以进一步查看这里这篇微文:【希尔伯特旅馆悖论】
十一、1928年:博弈论的创立
博弈论中寻求决策
约翰·冯·诺伊曼(John von Neumann)美国数学家,现代计算机与博弈论的重要创始人。1928年发表“关于伙伴游戏理论”提出两人零和博弈的极小极大定理。他首次证明了博弈论基本定理,即“每个矩阵博弈都能通过引进混合策略而被严格决定”,现代博弈论正式诞。他讨论了合作对策问题,特别是三人零和博弈中有两方联合的情形,结果表明在附加条件下,N人博弈问题的解存在且唯一。

图15:冯诺依曼
十二、1931年:范内瓦·布什与微分分析机
信息时代的教父
万尼瓦尔·布什(Vannevar Bush)美国著名工程师,发明了世界上第一台模拟电子机械计算机“微分分析机”。这台装置与现代的计算机很不一样,它没有键盘,占地几十平方米,看起来有点像台球桌,又有点像印刷机。分析仪有几百根平行的钢轴,安放在一个桌子一样的金属框架上,一个个电动机通过齿轮使这些轴转动,轴的转动模拟数的运算。在第二次世界大战中,美军曾广泛用它来计算弹道射击表。

图16:微分分析机
十三、1936年:邱奇与λ演算
编程语言的基石
阿隆佐·邱奇(Alonzo Church,美国数学家)和他的学生斯蒂芬·科尔·克莱尼引入λ演算,这种演算可以用来清晰地定义什么是一个可计算函数,邱奇运用λ演算给出判定性问题的一个否定,后来根据“邱奇-图灵论题”证明了λ演算与图灵机是等价的。

图17:阿隆佐·邱奇
十四、1936年:菲尔兹奖
数学界的诺贝尔奖
费尔兹奖(Fields Medal),正式名称为国际杰出数学发现奖,是一个在国际数学联盟的国际数学家大会上颁发的奖项,每四年评选2-4名有卓越贡献且年龄不超过40岁的数学家。
约翰·查尔斯·菲尔兹(John Charles Fields)加拿大数学家,菲尔兹最为人所知的成就是他设立的菲尔兹奖,这奖项被誉为数学界的诺贝尔奖。

图18
奖章由正面有古希腊科学家阿基米德右侧头像。在头像旁刻上希腊文” ΑΡΧΙΜΗΔΟΥΣ”,意思为“阿基米德的(头像)”,还有一句拉丁文” TRANSIRE SUUM PECTUS MUNDOQUE POTIRI”,意为“超越他的心灵,掌握世界”。
十五、1936年:图灵与图灵机
现代计算机之父
图灵机(Turing machine)又称确定型图灵机,是英国数学家艾伦·图灵于1936年提出的一种抽象计算模型,其更抽象的意义为一种数学逻辑机,可以看作等价于任何有限逻辑数学过程的终极强大逻辑机器,能模拟人类所能进行的任何计算过程。
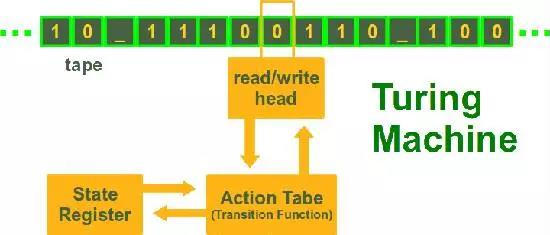
图19:图灵机组成
图灵机可以观看此文中的视频:【计算机之父:阿兰·图灵】—纪念诞辰 105 周年
十六、1946年:电子数值积分计算机
世界上第一台通用计算机
电子数值积分计算机简称ENIAC,它是图灵完全的电子计算机,能够重新编程,解决各种计算问题。ENIAC为美国陆军的弹道研究实验室所使用,用于计算火炮的火力表。
它的计算速度比机电机器提高了一千倍,这是一个飞跃,之前没有任何一台单独的机器达到过这个速度。除了速度之外,ENIAC最引人注目的就是它的体积和复杂性。它包含了17468个真空管、7200个晶体二极管、1500个继电器、10000个电容器,还有大约五百万个手工焊接头,重量达27吨。占地167平方米,耗电150千瓦,有传言说,每当这台计算机启动的时候,费城的灯都变暗了。

图20:在 ENIAC 上编程
十七、1948年:香农与信息论
改变了整个时代的理论
克劳德·香农(Claude Shannon)美国数学家,密码学家,被称为“信息论之父”。1948年发表《通信的数学理论》作为现代信息论研究的开端,在该文中,香农给出了用来描述随机事件不确定性度量信息熵的定义。

图21:克劳德·香农
本人水平有限,疏忽错误在所难免,还请各位老师和朋友多提宝贵意见,帮助我改进这个系列,本人也会不断修订完善的。您的关注和转发就是鼓励我继续前行的最大动力,感谢感谢!
参考资料:维基百科,百度百科,《数学之书》,《可计算知识时间轴图》,《数学史辞典》,图自网络,如有不妥,联删。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











