宇宙之大,粒子之微,火箭之速,化工文巧,地球之变,生物之谜,日用之繁等各个方面,无处不有数学的重要贡献。——华罗庚
一、1950年:图灵测试
“我准备探讨'机器能思考吗'这个问题”
图灵测试,是现代计算机之父阿兰—图灵在1950年提出的,该测试是指人(多人)在与被测试者(一个人和一台机器)隔开的情况下,通过一些装置(如键盘)向被测试者随意提问。问过一些问题后,如果测试人中超过30%的人不能根据答复确认被测试者哪个是人,哪个是机器,那么这台机器就通过了测试,并被认为具有人类智能。
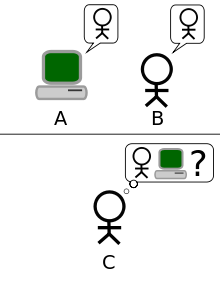
图1:图灵测试一个标准的模式:C使用问题来判断A或B是人类还是机械。
二、1950年:纳什平衡
两害相权取其轻,两利相权取其重
纳什平衡(Nash equilibrium),在博弈论中有重要地位,以美国数学家约翰·纳什(John Forbes Nash Jr.)命名。如果某情况下无一参与者可以通过独自行动而增加收益,则此策略组合被称为纳什均衡点。
注:感兴趣观看视频《什么是纳什均衡》或《博弈的乐趣 - 海盗分赃问题》
其经典的例子就是囚徒困境:一个案子的两个嫌疑犯被分开审讯,警官分别告诉两个囚犯,如果你招供,而对方不招供,则你将被立即释放,而对方将被判刑10年;如果两人均招供,将均被判刑2年。如果两人均不招供,将最有利,只被判刑半年。于是两人同时陷入招供还是不招供的两难处境。但两人无法沟通,于是从各自的利益角度出发,都依据各自的理性而选择了招供,这种情况就称为纳什均衡点。
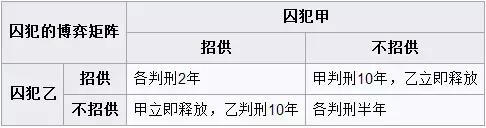
图2:囚徒的博弈矩阵
三、1950年:数值计算天气预报
来自多年以来科学知识和技术发展的持续积累
气象学家查尼(Jules Charney)与数学家冯·诺依曼(John von Neumann)等简化了所用的数学模型,并由第一部通用电脑——电子数值积分计算机(ENIAC)执行,终于第一份电脑计算的数值天气预报在1950年出现了。随着硬件运算能力增加、数值天气模式技术改良及天气观测数据数量和质量的改进,预报的准确度大大提升。

图3:全球数值天气预报模式的三维网格示意图
四、1952年:细胞自动机
简单模式生成大千世界
细胞自动机又称元胞自动机(Cellular automation)是一种离散模型。它是由无限个有规律、坚硬的方格组成,每格均处于一种有限状态。整个格网可以是任何有限维的,同时也是离散的。每格于t时的态由t-1时的一集有限格的状态决定。每次演化时,每格均遵从同一规矩。

图4:细胞自动机Rule 30示例
五、1954年:国际单位制的诞生
测量、计量工作的“宪法”
1954年第10届国际计量大会决定,国际性的单位制应以六个基本单位为基础,能够用于测量温度、可见光辐射、机械及电磁物理量。建议中的六个基本单位分别为:米、千克、秒、安培、开尔文和坎德拉。 1971年,国际单位制再添一个基本物理量──以摩尔来表示物质的量。
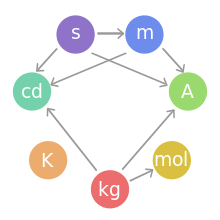
图5:七个国际单位制基本单位的相互定义关系
六、1954年:钱学森与《工程控制论》
自动控制与系统科学领域的经典著作之一
钱学森《工程控制论》的出版,把控制论的基本理论和方法推广运用到工程控制系统,是工程控制论的奠基之作。

图6:《工程控制论》封面与钱老
七、1957年:FORTRAN编程语言
第一个编译型语言
FORTRAN源自于“公式翻译”(Formula Translation)的缩写,是一种编程语言。1957年由IBM开发出,是世界上第一个被正式采用并流传至今的高级编程语言。Fortran语言是为了满足数值计算的需求而发展出来的。

图7
FORTRAN发明的年代还没有键盘与显示屏,代码必须使用打卡机打在打孔卡(punch card)上。图中显卡片上的1-5行、第6行与73-80行被使用过。
八、1966年:陈景润的(1+2)
哥德巴赫猜想研究上的里程碑
陈景润主要研究解析数论,1966年在简陋件下钻研数学,并发表《大偶数表为一个素数及一个不超过二个素数的乘积之和》,所发表的成果也被称之为陈氏定理。
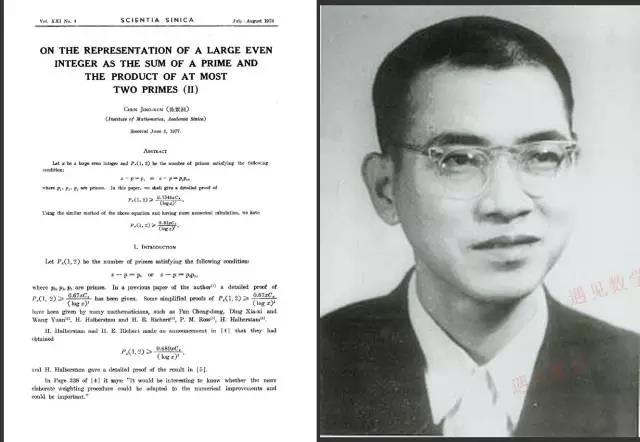
图8:论文摘要及陈景润
九、1963年:蝴蝶效应
即使细微如蝴蝶鼓舞,也能煽动千里之飓风
爱德华·诺顿·罗伦兹(Edward Norton Lorenz)美国数学与气象学家,他在使用计算机程序来计算他所设计来模拟大气中空气流动的数学模型发现,如果对初期某一个变数的小小变异,会影响到最后的结果,并可能发生很大的差异。1963年发表《决定性的非周期流》论文指出可求出无限解的数学模型,被称为“洛伦茨吸引子”(Lorenz attractor)。后又用了更加有诗意的蝴蝶来解释这个效应:“一只蝴蝶在巴西轻拍翅膀,可以导致一个月后德克萨斯州的一场龙卷风。”

图9:ρ=28和28.1时的轨迹,刚开始两条轨迹几乎重合,但一段时间之后分离就变得明显了。
十、1966年:数据结构
算法+数据结构=程序
两位获图灵奖的计算机科学家尼克劳斯·维尔特(Niklaus E. Wirth)和东尼·霍尔(Tony Hoare)提出了数据结构的概念,扩大了程序设计的能力。在计算机程序设计的过程里,选择适当的数据结构是一项重要工作。许多大型系统的编写经验显示,程序设计的困难程度与最终成果的质量与表现,取决于是否选择了最适合的数据结构。

图10:维尔特和东尼·霍尔
十一、1972年:HP-35第一台手持计算器
当时机械设计、顶尖的技术、算法开发及应用创新的巅峰之作
HP-35型科学计算器是惠普公司于1972年推出的世界上第一种手持式科学计算器。使用发光二极管作为显示设备,可以显示10位数字,进行加减乘除、三角函数、指对数运算等功能。因为一共拥有35个按键而得名。它能把计算尺的所有功能精确到10位数字精度,而且能够在200位十进制范围运行小数点或10次幂的指数。正是这些功能的结合,让已经被几代工程师和科学家所使用的计算尺最终退出了历史舞台。

图11:在HP-35型上显示π
十二、1973年:布莱克-舒尔斯模型
全球金融市场的标准模型
费雪·布莱克(Fischer Black)和迈伦·舒尔兹(Myron Scholes)给出了对股票期权进行估值的数学方法(Black-Scholes Formula),此公式问世后带来了期权市场的繁荣。该公式被广泛使用,虽然在很多情况下被使用者进行一定的改动和修正。很多经验测试表明这个公式足够贴近市场价格,然而也有会出现差异的时候。

图12:布莱克-舒尔斯模型
十三、1974年:魔方
世界上最流行的智力玩具之一
魔方(Rubik's Cube)为由匈牙利建筑学教授暨雕塑家鲁比克·艾尔内于1974年发明的机械益智玩具,是匈牙利的建筑学和雕塑学教授,为了帮助学生们认识空间立方体的组成和结构,所以他自己动手做出了第一个魔方的雏形来,其灵感是来自于多瑙河中的沙砾。

图13:1980年,魔方套装,在匈牙利Ideal Toys公司制造的玩具
十四、1975年:分形(Fractal)
大自然的几何学
本华·曼德博(Benoît B. Mandelbrot)1975年出版了关于分形几何((Fractal Geometry)的专著《分形、机遇和维数》,标志着分形理论的诞生。

图14:曼德尔布罗特集合
十五、1976年:丘成桐与卡拉比猜想
“用苦功而非天才”
丘成桐(Shing-Tung Yau)是公认的当代最具影响力的数学家之一,1976年,丘成桐解决关于凯勒—爱因斯坦度量存在性的卡拉比猜想,其结果被应用在超弦理论中,对统一场论有重要影响。
他的工作深刻变革并极大扩展了偏微分方程在微分几何中的作用,影响遍及拓扑学、代数几何、表示理论、广义相对论等众多数学和物理领域。

图15:丘成桐本人
十六、1977年:公开密钥算法
标志着现代密码学的诞生
1977年,MIT的三位数学家Rivest、Shamir 和Adleman设计了一种利用大质数保护密文的算法,可以实现非对称加密。这种算法用他们三个人的名字命名,叫做RSA算法,也就是公开密钥算法(非对称密钥)。RSA加密利用了单向函数正向求解很简单,反向求解很复杂的特性,将两个很大的质数相乘对计算机而言,是非常简单的,但是反过来把乘积还原为之前的两个质数就非常困难了。
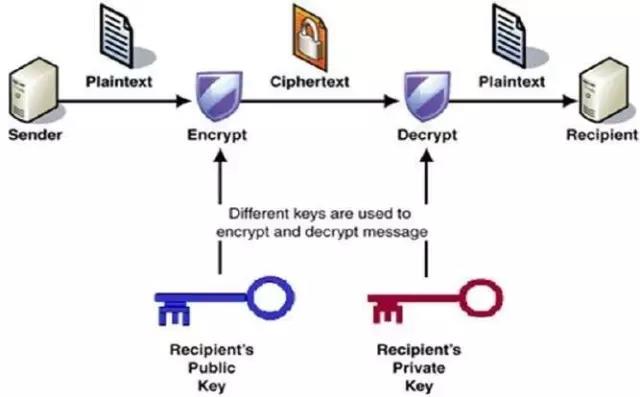
图16:希尔伯特的23个问题
十七、1980年:有限单群分类问题
标志了对所有有限对称性系统理解的开端
因为群在数学上的重大作用,对所有有限单群进行分类的问题,后经过世界100位数学家共同努力,在1985年完成。结果有18个有限单群家族,再加上26个散在单群。
图17:有限单群分类
十八、1995年:费马大定理的证明
20世纪数学一个美妙的句点
费马大定理历经三百多年的历史,最终在1995年被英国数学家安德鲁·怀尔斯(Andrew Wiles)彻底证明。费马大定理的证明涉及好几个近代的数学分支,包括代数数论中的椭圆曲线和模形式,以及群论中的伽罗瓦理论。

图18:怀尔斯本人
十九、2000年:千禧年大奖难题
与百年前希尔伯特23个历史性数学难题呼应
千禧年大奖难题(Millennium Prize Problems)是七个由美国克雷数学研究所于2000年5月24日公布的数学难题,解题总奖金700万美元。每解破一题的解答者,会颁发奖金100万美元。
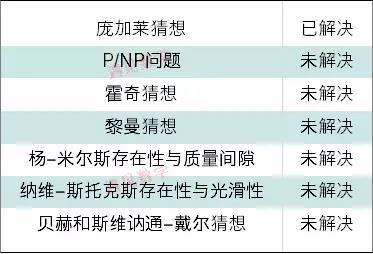
图19:Millennium Prize Problems
迄今为止,在七个问题中,庞加莱猜想已经被俄罗斯数学家格里戈里·佩雷尔曼(Grigori Yakovlevich Perelman)在2003年证明了它的正确性,而其他六道难题仍有待数学家研究探索。
数学与计算简史共10篇微文,现在暂时算是一个完结吧。该系列所涉及事件也只是在历史长河轻取一瓢而已,无法涵盖千万分之一。不过现在迈出了第一步,制作了第一个版本,未来会继续完善和补充,各位老师和朋友有指正和建议还请直接联系我们。(微信: meetmath_axiom)。【遇见数学】正在设计合集和海报,敬请关注!感谢阅读和支持!
参考资料:维基百科,百度百科,《数学之书》,《可计算知识时间轴图》,《数学史辞典》,《数学之旅》,图自维基/网络,如有不妥,联删。
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











