
图1
给我最大的快乐,不是已懂的知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登!——卡尔·弗里德里希·高斯
卡尔·弗里德里希·高斯(Gauss),为历史上最著名的数学家之一,与阿基米德,欧拉,牛顿被公认为人类史上最杰出的四位数学家。
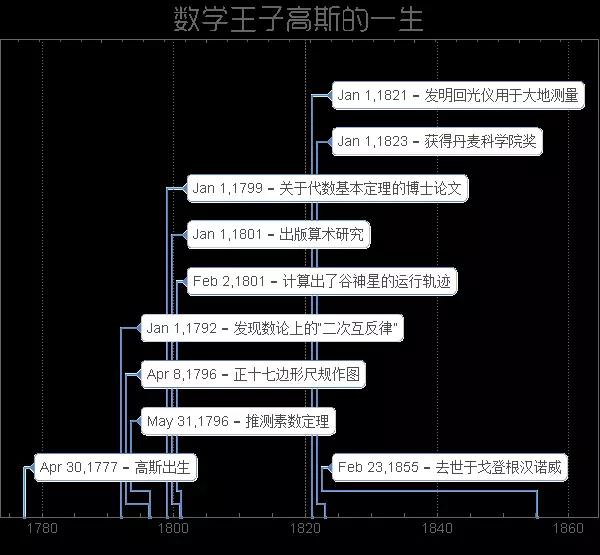
图2
高斯从小在数学上就具有高度才华,还不到三岁,他趴在一旁看作为工头的父亲计算工人的薪水,父亲好不容易算出来后,小高斯却说父亲算错了,并告诉父亲正确答案。高斯爸爸于是怀疑地再算一次,结果真的是高斯心算的总数。
高斯的成就,一方面莱斯天赋,另一方面来自于自身的勤奋。少年因家境贫寒,冬天为了节省燃料的开销,高斯的父亲就会要求高斯早早早上床睡觉,但是小高斯很喜欢看书,于是将大头菜中心挖空,塞进棉布成当灯芯,淋上油脂在微弱的灯光下读书到深夜。

图3
高斯上学后,更表现了他优异的思考能力。有一天,他的小学老师布特纳(Buttner)要求全班同学算出 1+2+3+......+98+99+100等于多少?老师的本意是想难为下这些刚学算术调皮的学生们。但是当老师话音刚落,高斯就解了出来,说出最后的结果为5050。并在老师的惊讶中解释计算的过程,他找到了等差级数的对称性:
1+2+3+……+98+99+100
100+99+98+……+3+2+1
-------------------------------------------------------
101+101+101+……+101+101+101
=101×100=10100,再将10100÷2=5050得到答案。
特纳老师认为遇到了数学神童,自己出钱购买高等算术来让高斯研读。后来由经费迪南公爵资助,让他有机会受高深教育。
希腊的数学已经能用圆规和无刻度直尺画出正3,4,5,15边形,如下

图4
但是随后的两千多年间,没有人能以直尺和圆规做出正11,13,14,17边形。1796年,高斯在18岁时候便解决了两千多年以来的这个几何难题,发表了《关于正十七边形作图的问题》。

图5(注:图自网络)
他以此为自豪,希望能将正十七边形刻在他的墓碑上。然而,最后刻上确实一颗十七角星。原来是负责刻纪念碑的雕刻家认为,如果是正十七边形的话,那跟圆就无法区分了。

图6
从24岁开始,高斯开始研究天文学,1801年,意大利天文学家发现在火星和木星之间有一颗新星,它被命名为谷神星。高斯用设计出的计算星球轨道的方法准确预测了行星的位置。
1830年高斯与物理学家威廉·爱德华·韦伯密切合作,在电磁学方面推动了电报的发展。下图为纪念两位伟大科学家的雕像。

图7
1855年,77岁的高斯在睡梦中心脏病发安详的去世了。
高斯自我高标准的要求与执着,对待学问十分严谨,只将自己认为十分成熟的成果公布出来。以至于有数学家甚至批评高斯,如果能早些所发布出所研究的成果,数学的发展要先进半个世纪或更多时间。这样阿贝尔和雅克比可以从接过高斯所停留的地方继续前行。
在过世22年后,汉诺威王颁给高斯一个纪念奖章,上面刻着“汉诺威王乔治V. 献给数学王子高斯”。从此,高斯就有了“数学王子”之称。
参考资料:维基中文。
另附文中所提到科学家时间轴线图:
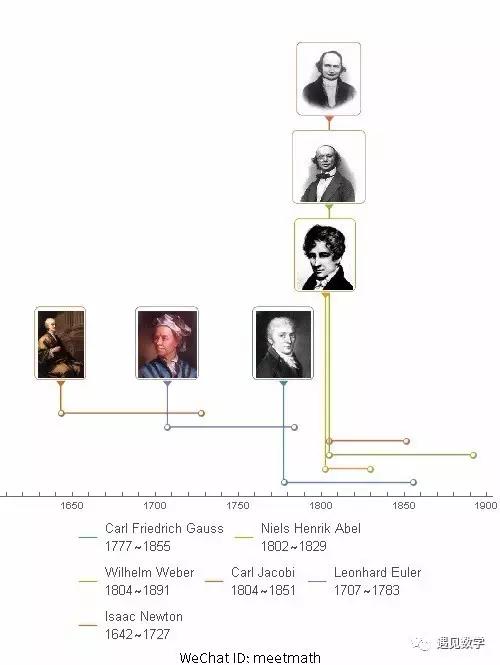
图8
声明:文章转自【遇见数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











