18世纪数学的发展是以欧拉为中心的,故事的主要场景是瑞士和俄国,大约是在纳皮尔(Napier)经历宗教改革的骚乱、安特卫普(Antwerp)对新教徒疯狂迫害的时候,一位名叫雅克·伯努利(Jacques Bernoulli)的人随着大批流亡者逃到了法兰克福(Frankfort)。后来的事实说明,失去他可是比利时(Belgium)的一大不幸。
1622年,这位雅克·伯努利的孙子在巴塞尔定居——在这个瑞士的边境城市,伯努利家族注定要为这个收留他们的国家带来荣耀。他们所取得的空前的数学成就,是遗传力量或者早期家庭影响的有力证据。在这个家族中至少有9位家庭成员在数学或物理上取得了卓越的成就,并有4位获得了巴黎科学院的特别表彰,其中最出色的2个人是雅各(Jacob)和约翰(John),他们是那位逃出安特卫普的雅克·伯努利的曾孙。雅各是这个大家庭的第五个孩子,比他小13岁的约翰排行第10,他们两人依次成为巴塞尔大学数学教授。
经过大量实验和游历之后,长兄雅各最终确定了自己成为分析数学家的非凡职业,他的父亲希望他致力于神学,并曾经因此一度禁止他学习数学和天文学。但是与生俱来的天赋驱使他一生都在发展、完善帕斯卡和牛顿开创的学科。等角螺线是他的众多发现之一,而且可能也是他最美妙的一个发现。
等角螺线存在于蜘蛛网的图案中、岸边的贝壳上以及遥远星云的回旋曲线里。在数学上,等角螺线与几何中的圆以及分析里的对数有关。圆形曲线在任何一点处与其半径的夹角总是直角;等角螺线在任何一点处与其半径的交角也是确定的,但并不是直角。等角螺线有着凤凰一般的美妙特性:对它进行与焚烧或撕碎等价的数学变换,它将毫发无损的再现!对于老年时期的伯努利来说,这种曲线就好像是他生活和信仰的象征。遵照他的意愿,人们在他的墓碑上镌刻着这条曲线以及附言:纵使改变,依然故我(Eadem mutate resurgo)。
雅各的弟弟约翰(1667-1748)追随着他的脚步,不断地为分析添加如今属于微分方程的新内容,他在自己的工作中大胆的使用了负数和虚数,进而认识到纳皮尔曾经希望自己用“这个量的幽灵”为数学奉献“丰厚的回报”,只是他的精力完全被对数占据了,所以未能如愿。约翰的儿子丹尼尔·伯努利(Daniel Bernoulli)和尼古拉斯·努利(Nicolas Bernoulli)也是非常有才华的数学家,而且正是由于在大学里受到了他们的影响,欧拉才发现了自己的天职。
列奥纳多·欧拉(Leonard Euler,1707-1783)是居住在巴塞尔附近的一位牧师的儿子,在父亲给他讲授一些基本原理的时候,他在数学上的天资立刻显露出来,他在很小的时候就被送进巴塞尔大学,并引起来约翰·伯努利的注意。在这样一位老师的启发下欧拉很快成长起来:他17岁获得了理学硕士学位;他关于笛卡尔体系与牛顿体系之比较的见习演讲赢得了很高的赞誉。
欧拉的父亲曾热切的希望他成为一名牧师并亲自指导他学习神学,但是与伯努利的父亲不同,当发现儿子天赋在另外一个领域之后,他就放弃了自己的观点,使列奥纳多得以继续追求自己热爱的事业。19岁时,欧拉将两篇论文寄到了巴黎科学院,一篇是关于船桅定位的,另一篇则是关于声音的哲学探讨,这两篇论文标志着他辉煌事业的开端。
大约在这个时候,由于未能得到巴塞尔大学某个空缺教授的职位,欧拉感到非常失望并决定离开自己的祖国。1727年,也就是牛顿去世的那一年,欧拉前往圣彼得堡(St. Petersburg)投靠几年前来到那里的年轻的伯努利兄弟。在去俄国的路上,欧拉得知尼古拉斯·伯努利已经因为北方严酷的气候而去世;在踏上俄国土地的那一天,建立圣彼得堡科学院的女皇叶卡捷琳娜一世(Empress Catherine I)去世了——这件事最初曾预示着科学院的解散。
心灰意冷的欧拉打算放弃从事智力劳动的希望去参加俄国海军。但令人高兴的是,1730年由于公共事务方面的变化,欧拉得到了自然哲学方面的职位,这是数学的一大幸事。1733年丹尼尔·伯努利离开圣彼得堡科学院,欧拉继任了他的职位;就在这一年,他与一位瑞士女士、女教师葛塞尔(Mademoiselle Gsell)结婚了,葛塞尔的父亲是由彼得大帝带到俄国的画家。
2年后,欧拉出色的展示了自己的能力:他用三天时间解决了科学院成员们急需但又认为没有几个月的辛苦劳动就不可能解决的问题。这项工作的巨大压力致使欧拉一只眼睛失明,尽管遭遇这一次灾难,欧拉在数学研究和发现上却非常成功,似乎每一次进展都在鼓舞他更进一步的努力。大约在30岁的时候欧拉得到了大家的公认并获得了巴黎科学院的表彰,同时分享这项荣誉的还有丹尼尔·伯努利和我们的同胞科林·麦克劳林(Colin Maclaurin)。他们的获奖论文是关于海洋潮汐的研究,麦克劳林的工作中包括了关于椭球平衡问题的一个著名定律;欧拉的论文则大大拉近了解决著名的天体运动问题的希望。
1741年夏天普鲁士国王腓特烈大帝(King Frederick the Great)邀请欧拉到柏林居住。欧拉接受了这一邀请并一直在柏林居住到1766年,刚到柏林欧拉就收到了从雷申巴赫(Reichenbach)行宫寄来的皇室信件,并立即被引荐给太后,这位太后很喜欢与杰出人士交谈。尽管太后试图让欧拉感觉轻松一些,但欧拉除了发出一些单音词之外从来没能真正进行任何交谈。一天当她问道这个问题的原因时,欧拉回答说:“女士,这是因为我才从一个说话就会被吊死的国家过来。”在柏林居住期间,欧拉给安尔哈特·德绍公主(Princess of Anhalt Dessau)写了一系列关于自然哲学的著名信件或者说讲稿,据说这位公主急于得到这位伟大老师的指点。这些信件是清晰易懂,趣味盎然的讲义的典范,并且值得注意的是,欧拉在其所有其他文学兴趣之外,还能找到时间来做如此详细的基本工作。
欧拉的寡母也在柏林住了11年,享受儿子殷勤的照顾以及人们对他儿子的敬仰与赞扬。欧拉与柏林科学院院长莫佩蒂(M. de Maupertuis)十分亲密。莫佩蒂虽然来自法国布列坦尼(Brittany),但与笛卡尔学说相比他更强烈支持牛顿的哲学,他的影响对于当时仍然不愿接受牛顿观点的欧洲大陆来说是十分重要的。莫佩蒂对最小作用原理的喜爱给欧拉留下了深刻的印象,欧拉极其有效地将这个原理运用于解决力学问题。
有一个故事可以说明当时人们对欧拉是何等的崇敬。1760年,一支俄国军队入侵德国并掠夺了一个属于欧拉的农场。将军知道这件事之后立即赔偿了欧拉的全部损失,伊丽莎白女王知道这一情况后又送给欧拉4000弗罗林(florins)。
1766年欧拉回到圣彼得堡,他将在这里度过剩余的岁月,但是到达圣彼得堡不久他的另一只眼睛也失明了。有一段时间欧拉不得不在石板上写大字进行运算,后来他的学生和孩子们负责抄写他的工作,准确地记录他口述的论文。这是一项了不起的工作,其工作量和原创性都令人惊叹不已,双目失明使他发展出来一种不可思议的熟练的运算能力,一种通过心算进行庞杂运算的罕见天赋。据说有一次他的两个学生求某个级数的前17项和,但两人所得的结果在第50位有效数字上相差了一个单位。欧拉通过心算检查这两位学生的结果,人们发现它的裁决是完全正确的。
1771年,欧拉居住的城镇发生了一场大火,火势蔓延到欧拉的房子。欧拉的巴塞尔同乡彼得·格林姆(Peter Grimm)冲进火焰,找到双目失明的欧拉并把它扛到了安全的地方。尽管所有的书籍和家具都被烧掉了,但欧拉宝贵的手稿却得以幸存,在接下来的12年多的时间里,欧拉继续超负荷的一直工作到去世的那一天,这时他76岁。
与牛顿以及许多其他人一样,欧拉也是一个才华横溢的人。他研究过解剖学、化学和植物学,与传说中的莱布尼茨一样,欧拉也能从头到尾背诵《埃涅伊德》(Aeneid),甚至还记得他常用的那个版本中每一页的第一行和最后一行。这种能力似乎来自他惊人的专注,而这种专注正是创造能力的主要组成部分,牛顿自己的例子已经证明了这一点,当他的全部心智都陷入沉思时,任何外界事物都无法干扰到他。
和悦的性情,简朴适度的生活方式是欧拉的特征。他很喜欢孩子,家就是他的快乐。尽管遭受磨难,他始终开朗、乐观,并拥有旺盛的精力,正如他的学生福斯(M. Fuss)所说,“他的虔诚是理性的、真挚的,他的奉献精神是强烈的。”
在一篇非专业性文章中是不可能恰当处理欧拉的数学工作的,但是如果说牛顿是一位民族英雄,那么欧拉就是一位数学英雄;牛顿就像阿基米德,欧拉则是毕达哥拉斯。欧拉关于一些物理问题的工作也非常出色——不过这是因为这些物理问题的数学模型抓住并始终吸引着他的注意力。他的乐趣就是在纯智力王国中思索,在这里他是所有分析数学之王。甚至几何学,甚至对于直线和图形的研究都不能使他改变:他的终极目的就是完善微积分和分析。他的思想在这列通往新的数学冒险活动的列车上如此自然的驰骋,他甚至能在维吉尔(Virgil)的诗里找到启发哲学研究的观念。这些数学研究就是一次次的冒险,让他那些谨慎的追随者们,有时快乐的欢呼,偶尔又会愤怒的谴责。古希腊时期孕育的萌芽以及后来纳皮尔、牛顿和莱布尼茨工作的全部光彩现在得以展现。在此,我们引用一个简短的公式作为欧拉成就的象征:
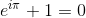
菲利克斯·克莱因(Felix Klein)不是曾经说过全部的分析都汇聚于此吗?这里的每一个符号都有自己的历史——最主要的整数0和1;最重要的数学关系+和=;希波克拉底发现的π;表示-1的“不可能”的平方根的符号i;以及纳皮尔对数的底e。
注:文章选载自高等教育出版社《数学的世界Ⅱ》,J.R.纽曼编,李文林等译
声明:文章转自【好玩的数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











