图1
“24点游戏”是大家非常熟悉的数学益智游戏，它的游戏规则是：在除掉大小王之外52张扑克牌中任取4张牌，看能否在其间添加四则运算符号和括号得出24。其中A、J、Q、K分别代表数字1、11、12、13。
有两个与之相关的数学问题值是我们研究。从一副扑克牌中任取4张牌，一共有多少种可能的出牌组合？此其一。在所有可能的出牌中，有多少种组合是可以算出24的？此其二。
第一个问题是一个排列组合问题，对于所选的4张牌有以下5种情况：
① 4张牌点数都不相同，共有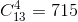
种组合。
② 其中2张牌点数相同，另两张牌点数都不同，共有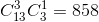
种组合。
③ 其中2张牌点数相同，另2张牌点数也相同，共有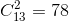
种组合。
④ 其中3张牌点数相同，另一张牌点数不同，共有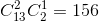
种组合。
⑤ 4张牌点数都相同，共有13种组合。
所以，所有的可能情况数为：
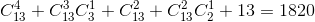
在旅美科普作家蒋迅与数学史专家王淑红最新出版的数学科普著作《数学都知道》第一分册中提到了一个更简洁的计算公式：
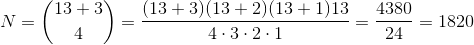
其中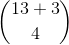
即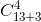
。
如此简洁的一个公式是如何得到的呢？这需要用到组合数学中的隔板法。
用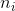
表示点数为i（i=1,2,3,…,13）的扑克牌在四张牌中出现的次数，那么“24点游戏”的所有可能出牌组合数即为方程
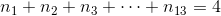
的非负整数解的个数。令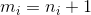
，那么“24点游戏”的所有可能出牌组合数即为方程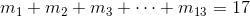
的正整数解的个数。这个问题又等价于把17个相同的小球放入13个盒子中，每个盒子至少一个球，问有多少种放法？设想把17个小球排成一排，则小球与小球之间有16个空隙，那么问题又相当于在16个空隙中插入12块隔板的方法数。显然有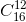
种插入方法，亦即
。
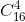对于第二个问题，可能与你所期待的相反，并没有什么快捷的方法得出答案，而只能通过枚举的方法一个一个进行判断。根据计算机编程得出的结果，在这1820种可能的组合中，有1362种组合是可以算出24的，即有458种组合算不出24。进一步的研究表明，在所有1362种可解组合中：
有515 种组合有且只有1个解；
有427种组合有且只有2个解；
有216种组合有且只有3个解；
有125种组合有且只有4个解；
有31种组合有且只有5个解；
有17种组合有且只有6个解；
有17种组合有且只有7个解；
有8种组合有且只有8个解；
有2种组合有且只有9个解；
有3种组合有且只有10个解；
最后，只有（2，4，8，10）有11个解。
以上，有且只有1个解的意思是，比如（1，1，1，8）只有1种方式算24：（1+1+1）×8=24，又比如（1，1，2，6）只有2种方式算24：(1+1)×6×2和(2+1+1)×6，即有且只有2个解。
现在人们玩“24点游戏”往往把乘方、开方、阶乘等算符也用上，在这样的情况下又有多少中可解的组合呢？这个问题就留给各们读者去思考吧！
（感谢蒋迅老师为本文提供指导意见）
声明：文章转自【好玩的数学】微信公众号，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。
