与美食一样,数学也有味道,不同的数学有不同的味道。
按照西方世界的传统,学界常把数学大致划分为代数、分析与几何三味。从17世纪中叶始,一门蕴含着独特品位的新数学从几何的内部出现了。到今天,这门年轻的数学已经广泛而深刻地与代数、分析、几何、集合论甚至物理相连,改变了现代数学乃至科学的内容、结构与叙事风格,并为几乎所有的数学部门服务着。它就是我们故事的主角——拓扑(topology)。
英文topology一词源自德文单词Topologie。后者则由德国数学家李斯亭(Johann Benedict Listing)在1847年的著作[1]中创造自希腊单词τόπος(topos,位置)与λόγος(logos,研究)。至于中文“拓”、“扑”二字,则主要来源于我国1938年出版的《算学名词汇编》,其将德语Topologie音译为“拓拔”。后来,数学家江泽涵在40年代年翻译沙爱福(Herbert Seifert)与施雷发(William Threlfall)的名作Lehrbuch der Topologie(《拓扑学》)时,将标准译法“拓拔”改为“拓扑”,以表达“延拓、扑打”之意。
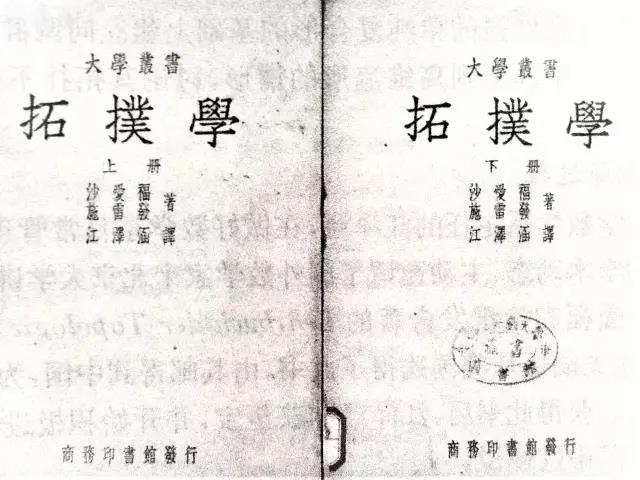
图1:江泽涵译著《拓扑学》封面。(图片来自《民国时期中国拓扑学史稿》)
数学史的研究已经向我们表明,拓扑在它的草创阶段蒙受了如下数学家的关照,他们是:笛卡尔(René Descartes)、莱布尼兹(Gottfried Wilhelm Leibniz)、欧拉(Leonhard Euler)、高斯(Carl Friedrich Gauss)与黎曼(Bernhard Riemann)等。本文试图介绍他们的与拓扑相关的工作,以期为读者描绘一幅拓扑史前史画卷。
一、何为拓扑
江泽涵之所以追求“延拓、扑打”的意象,是因为这一意象在相当程度上表达了这门学问的特征。我们不妨由此追问,究竟何为拓扑?
《现代汉语词典(第六版)》对“拓扑学”一词的解释为:数学的一个分支,研究几何图形在连续改变形状时还能保持不变的一些特征,它只考虑物体间的位置关系而不考虑它们的距离与大小。
在这一解释中尚有两个概念需进一步澄清。一是连续变形,二是不变特征。仅举一例。假设一圆周具有的充分的延伸性,可以保证它能够连续不断地被均匀撑大,但不被剪断或粘合。在整个连续变形的过程中,圆周长度与直径的比保持不变,为π。这一比值就是均匀撑大这一连续变形下不变的数值特征。然而,这一特定的连续变形显然过于苛刻。若在圆周撑大的过程中忽略均匀性,则可能得到椭圆或任意不规则的闭曲线*,这时原来的不变特征π就流失了。
* 注:闭曲线是首尾相接的封闭曲面。
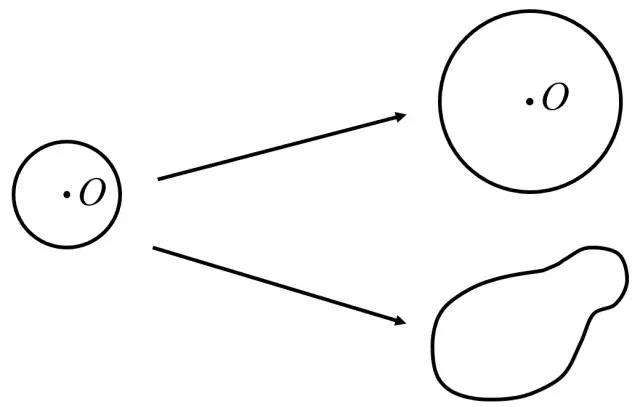
图2:在小圆周向大圆周的变形过程中,π值为不变量;在小圆周向不规则闭曲线的变形过程中,π值不为不变量。
因此,在相对一般的连续变形下,圆周率π并非不变特征,它受变形的影响而改变。而拓扑所关注的,是在任意的连续变形下仍能保持不变的特征,它们显然比圆周率、内角和这些特征更加基本。具有相等的不变特征的不同几何体被称为拓扑等价的。在后续介绍中,我们会详细涉及拓扑等价的物体与它们的不变特征,现仅举一广为人知的例子。提及拓扑,人们总会想起咖啡杯与甜甜圈。在咖啡杯连续向甜甜圈变形的过程中,许多几何特征都被破坏掉了,但有一个被人们成为亏格(genus)的特征保持不变(g = 1)。这体现为在整个变形过程中,物体上洞的数量始终为1。这时可以说咖啡杯与甜甜圈是拓扑等价的。可以想象,高脚杯与甜甜圈拓扑不等价,因为它们具有的拓扑不变量不同,甜甜圈有一个洞(g = 1),高脚杯没有洞(g = 0)。在这里,亏格g充当了指示剂,它指示了两几何体是否为同一拓扑(拓扑等价)。

图3:咖啡杯向甜甜圈连续变形的过程。在拓扑上,两者是等价的。(图片来自gmanetwork.com)
另一个需要揭示出来的最重要的隐含问题是:为什么拓扑关注这类特殊的不变特征?这恐怕这是出于数学家对相似性研究的追求。大自然往往把终极秘密隐藏在那些看起来风马牛不相及的事物的猝然的相似性中。在德比希尔(John Derbyshire)的科普著作[2]中,作者讲述了数学家蒙哥马利(Deane Montgomery)与物理学家戴森(Freeman Dyson)的相遇。这次相遇把素数的分布这样最纯粹的数学问题与复杂原子核能级分布那样最现实的物理现象扯上关系,就如同亏格把咖啡杯与甜甜圈联系在一起一样。
拓扑创立以来的百年间历史,就是数学家寻找、构造不同类型的不变特征,并据此判定不同层次的相似性的历史。
二、欧拉的工作
欧拉1707年生于瑞士巴塞尔(Basel),1783年死于俄国圣彼得堡(Saint Petersburg)。他极为高产的职业生涯在柏林(Berlin)与圣彼得堡展开,推动着当时全部数学部门的发展。
哥尼斯堡七桥问题(Seven Bridges of Königsberg)的解决是欧拉对拓扑的第一项贡献。在市面上任何一本关于图论的教材或科普书籍上都能找到该问题的来龙去脉。哥尼斯堡如今叫做加里宁格勒(Kaliningrad),是俄罗斯一块位于波罗的海(the Baltic)南岸的飞地,也是哲学家康德(Immanuel Kant)与数学家希尔伯特(David Hilbert)的故乡。如下图所示,有七座桥连接着河流两岸的城市与河中的岛屿。问,是否存在着一条路径,该路径通过所有七座桥,且每座桥只通过一次?

图4:哥尼斯堡七桥问题的图论模型。(图片来自wikipedia.org)
1736年,欧拉在论文[3]中将陆地用点代替,将桥用线代替,从而把哥尼斯堡七桥问题抽象成连通图问题。欧拉的结论是,不存在一条走遍七座桥但不重复的路径(如今该路径在数学上被称为欧拉路,就是人们常说的一笔画)。欧拉为这一问题建模的过程充分体现了拓扑“只考虑物体间的位置关系而不考虑它们的距离与大小”这一释义。这篇论文通常被当作组合拓扑研究与图论研究的起点。请思考:“不存在欧拉路”是否可以作为一种不变特征?如果是,它是什么条件下的不变特征呢?
多面体的欧拉定理是欧拉对拓扑的又一项贡献。在1750年的论文[4]中,欧拉确认,对任意凸多面体P,记其顶点数、棱数与面数分别为V(P)、E(P)与F(P),则总有
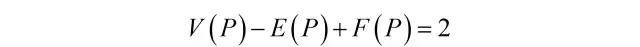
对于拓扑内涵敏感的读者应发现,虽然在这里欧拉并没有关注不同凸多面体之间是否存在连续变形,但他已经表明,数值2对不同凸多面体是不变的。记欧拉示性数χ(P) = V(P) − E(P) + F(P),实际上,对任意紧的可定向*曲面S,χ(S)都是拓扑不变量。换句话说,对于拓扑等价的几何体,其χ(S)相等;对于拓扑不等价的几何体,其χ(S)必不相等。人们可以据此对紧的可定向曲面进行分类(回忆高脚杯、咖啡杯与甜甜圈,根据亏格这一不变量,咖啡杯与甜甜圈是一类曲面,而高脚杯不是)。此外,从定理的内涵可以看出,变量V(P)、E(P)与F(P)与常量2都不涉及长度、角度或面积等度量性质,而仅仅是位置关系的表达。
* 注:“紧”的意思是该曲面上任意两点紧密相靠,没有间隙;“定向”的意思是可以对该曲面指定哪一面为正面,哪一面为反面,有些曲面是不可定向的。
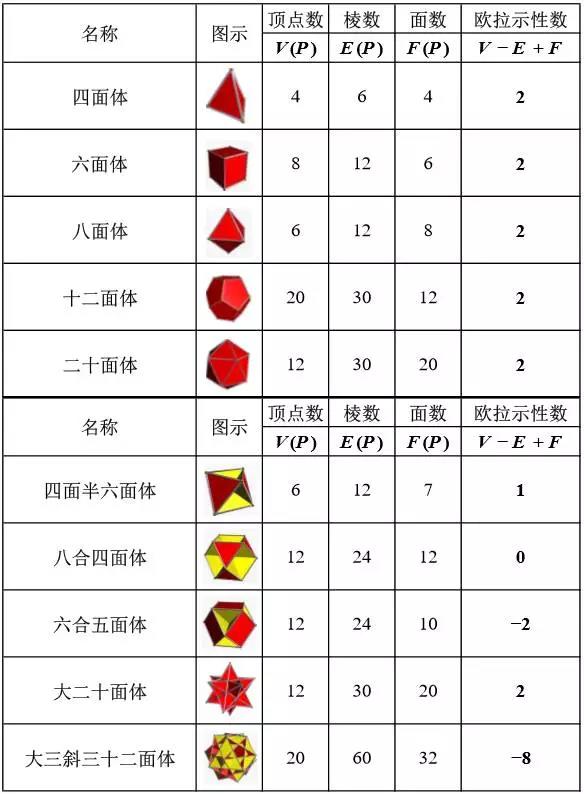
图5:一些多面体的欧拉示性数。
但凸多面体这一性质的发现,其功劳恐怕不能单单记在欧拉头上。1982年,美国数学家Pasquale Joseph Federico的数学史研究[5]表明,莱布尼兹作为外交家在巴黎(Paris)逗留时期(1672-1676),曾誊写过笛卡尔的一部关于多面体的著作《多面体研究》(De solidorum elementis)。虽然笛卡尔的手稿原件已经散佚,但莱布尼兹的抄本由Foucher de Careil公爵于1859年出版,见[6]。笛卡尔表明,在任何一个多面体中,各立体角之和等于8个立体直角。若将这一命题稍加改造,即可推导出多面体的欧拉定理。
对此,数学史家克莱因(Morris Klein)在[7]中评价道:几何图形的一个组合性质(多面体欧拉定理)跟欧拉的名字联系在一起,虽然笛卡尔在1639年就知道这一性质,并且通过笛卡尔未发表的手稿,莱布尼兹在1675年也知道这个性质。
至于莱布尼兹本人,则一直对用坐标研究几何的方法心怀不满。在[7]中,克莱因提醒我们莱布尼兹曾给惠更斯(Christiaan Huygens)写信,告诉后者他对一种不只关注数量的几何学充满热忱,可惜惠更斯不以为是。就像预想到二进制那样,莱布尼兹预想到位置几何、组合拓扑的可能性,他是一位真正的先驱。
总体来说,囿于历史的局限,早期的拓扑研究者们并没有意识到自己究竟在研究什么。他们的成果是零散的、肤浅的,甚至是错误的,有待进一步纠正与发展。但是,婴儿的第一步必定蹒跚,它的意义在于,迈出去。
三、高斯的工作
欧拉去世时,高斯只有6岁。与欧拉相比,高斯的工作更加职业与系统,对现代科学的影响也更大。高斯还是一位好老师,指导了戴德金(Richard Dedekind)与黎曼。他长时间在哥廷根大学(University of Göttingen)任教,开创了哥廷根学派,使这个德国小城一跃成为世界数学中心。

图6:第四套德国马克中的10马克纸币,正面人物为高斯,发行于1989至2001年。(图片来自wikipedia.org)
高斯未曾就拓扑问题直接发表意见,但他的几何思想,尤其是他继欧拉与蒙日(Gaspard Monge)之后关于曲面的研究,最深刻地改变了数学的面貌,预示着黎曼几何与现代微分几何的到来。高斯思想的核心是内蕴几何,它可以凝练地表达为:每一张曲面都是一个空间,同一个空间可以有不同的几何。
我们对一个事物的研究,一般总可以分为内蕴、外蕴两个角度。比如,内蕴地研究机动车的行驶状态,则发动机、变速箱、传动机构等状态参数是主要影响因素;而外蕴地研究机动车的行驶状态,路面情况就不能忽略。可见,内蕴从且仅从研究对象(如机动车)的内部出发,而外蕴反之。让我们回到几何的语境理解内蕴几何。请回想大学一年级高等数学课上的情形:为了解决球面上的计算问题,我们往往以以球心为原点建立的三维直角坐标系作为计算基础。这一做法的本质是把球面嵌入到三维欧氏空间,它类似于人们只有进入外太空,才能全局地观测地表的弯曲以及地球的形状。
在数学上,嵌入的结果就是,曲面上的度规*很自然地由欧氏空间的度规所诱导,曲面上的计算寄于欧氏空间之篱下。但只要我们能内蕴地在曲面上,而不是依赖外部空间给出度规的表达,就完全可以把曲面从它所在的背景空间中掏出来,把曲面上几何的研究集中在曲面本身。另外,如果曲面上度规的选取不唯一,就可以依据不同度规的选取得到完全不同的几何,显然,这些几何都是非欧几何。正是高斯的工作实现了解放曲面的这一理想。
* 注:度规相当于尺子。给定一特定的度规,相当于制作一把特定的尺子。显然用两把不同的尺子测量同一条线段,所得到的结果是不同的。所以说,不同的度规决定了不同的几何。配有笛卡尔坐标系的三维欧氏空间的度规为ds2=dx2+dy2+dz2。
如果要建立内蕴几何,就需要一套描述几何内在性质的内蕴几何量。前文提到,弯曲的性质似乎是外蕴的,因为只有从弯曲的表面跳出来才能发觉这一性质。但存在球面和柱面两种不同的弯曲的事实*仿佛又在提醒我们,应该存在一种内蕴弯曲。
* 注:这一事实是,柱面是可展曲面,球面是不可展曲面。可展的意思是可以展成平面。
在1827年著名的《关于曲面的一般研究》[8]中,高斯发现了曲面的一种内在性质——高斯曲率K,它由曲面第一基本形式*完全确定。随后高斯证明了一条定理,后来它被法国数学家博内在[9]中推广到一般曲面上由任一闭曲线C围成的单连通区域**,即在大范围微分几何中居于核心地位的高斯—博内定理(Gauss-Bonnet theorem)。鉴于此定理十分重要,且今后的介绍会经常返回到它,我们不妨花点力气将它写出:设M为紧的可定向二维曲面,D是M上由有限条光滑曲线组成且具有边界∂D的单连通区域,则总有
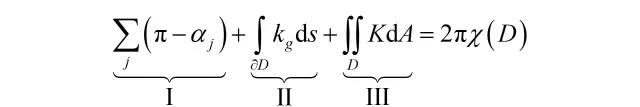
其中 αj 为边界顶点处的内角,kg 为每一条光滑曲线的测地曲率***,K为曲面M的高斯曲率。项I代表各顶点外角和,项II代表测地曲率在边界上的积分,项III代表高斯曲率在区域上的积分。式子右侧χ(D)为区域D的欧拉示性数。
* 注:曲面的第一基本形式用点和方向的函数表达曲面上最基本的内蕴量——弧长。
** 注:如果区域内的任意闭曲线能收缩成一点,那么该区域为单连通的。圆环、空心球等都不是单连通的。
*** 注:测地曲率是曲线上的内蕴曲率。
高斯—博内公式揭示了拓扑不变量欧拉示性数与曲面上内蕴曲率的积分之间的深刻联系,是拓扑不变量几何化的肇始。今后,我们将会看到形式更复杂的拓扑不变量首先通过欧拉示性数,继而通过(各种推广的、变形的)高斯—博内定理与曲面上的几何性质联系起来,从而简化了拓扑计算。百年后,物理学家爱因斯坦(Albert Einstein)对高斯1827年的工作评价道[10]:高斯对于近代物理理论的发展,尤其是对于相对论理论的数学基础*所作的贡献,其重要性是超越一切,无与伦比的……我实在很难想象其他任何人会发现这一理论。
* 注:广义相对论是宇宙的几何理论,它的数学基础是黎曼几何。后文将以图简述之。
1855年,高斯以77岁高龄在哥廷根去世。在他身后,黎曼已经整装待发了。
四、黎曼的工作
黎曼是高斯之后又一位现象级的数学家。他1826年生于当时的汉诺威王国(Kingdom of Hanover),1866年死于意大利塞拉斯加(Selasca),年仅39岁。从1851年发表博士学位论文算起,在短短15年的职业生涯中,黎曼将大量原创性的概念、方法与思想引入现代数学,从而被誉为第一位现代数学家。他的工作仍在启示着当今最前沿的数学研究。

图7:黎曼(1863年)与他的墓碑。(图片来自wikipedia.org)
与前辈同行不同,黎曼对拓扑的贡献是从他的复变函数论出发的。在博士学位论文《单复变函数的一般理论基础》[11]与1857年的《Abel函数的理论》[12]中,黎曼着力研究了复变函数*的几何性质。他认为,椭圆函数可以被认为是定义在曲面(环面)上的多值函数,因此为了对多值函数进行单值化,有必要研究曲面的连通性,随后横剖线**与连通阶的概念被引入了。直观上,需要数条横剖线才能将非单连通曲面变为单连通曲面。黎曼定义:一个非单连通曲面是n阶连通的,若恰好有n−1条横剖线将它变成单连通曲面。球面或圆盘是1阶连通的,因为它们本身即是单连通的。环面(甜甜圈的表面)是3阶连通的,因为需要2条横剖线才能将环面变成单连通的。
* 注:复变函数是以复数为自变量的函数,椭圆函数是一类复变函数。复变函数的研究属于分析学,是数学中发展相对完善的部门。
** 注:横剖线是两端点落在曲面边界上的不自交曲线。对于球面等闭曲面,它就退化成纬线一样的闭曲线。
可以证明,曲面的连通阶是一拓扑不变量,它与曲面的亏格完全等价:如果曲面的亏格为g,则其连通阶为2g + 1。在[12]中,黎曼已经把亏格作为可定向闭曲面的分类标准:如果两个闭曲面拓扑等价,则它们拥有相同的亏格。紧接着,黎曼得到了极为优美的黎曼—洛赫定理(Riemann-Roch theorem),这一定理通过亏格g,将曲面上的复分析问题巧妙地转换为纯代数问题,开拓扑连接分析与代数之先河。

图8:奠定黎曼几何基础的《1854演讲》讲稿,1868年出版。(图片来自deutschestextarchiv.de)
必须指出,黎曼并不仅仅是一位技巧高超的数学家,与高斯一样,黎曼也有传世的数学思想。1854年6月10日,28岁的黎曼就任哥廷根大学无薪讲师*一职。在就职典礼上,黎曼按高斯的要求,做了关于几何基础的震古烁今的演讲,讲稿于1868年以《论作为几何基础的假设》[13]为题出版。为了照顾在座的非数学系教员,黎曼在演讲中只提及了一个公式,然而这一直接继承了高斯的衣钵,发展了二维曲面上内蕴几何的演讲仍令许多人感到迷惑。1861年,35岁的黎曼写成一篇关于热传导的文章,期望借此获得巴黎科学院奖金,但最终失败。在这篇今天被称为《巴黎之作》[14]的文章中,黎曼进一步发展了他的几何思想。一般认为,[13]与[14]建立了19世纪最伟大的数学创造——黎曼几何。
* 注:无薪讲师制度是18世纪在德国高校形成的。无薪讲师性质类似于教授的私人助教。无薪指其薪资不由国家出资,而由听课学生支付。
内蕴几何的出现表明即便我们深处此山中,仍能通过内蕴的方法驱散迷雾,而不必刻意追求上帝视角。这就像布鲁诺(Giordano Bruno)或者哥伦布(Cristoforo Colombo)并没有进入太空,但他们仍用自己的方法发现地球是圆的。这一思想的载体就是高斯在曲面上的工作。黎曼比高斯更进一步的地方首先在于他对空间的看法,其次在于他的手段。他希望找到一种方案区分几何中那些先验的、拓扑的与经验的、度量的部分,从而使几何建立在那些先验上去。我不敢间下己见地认定黎曼的空间观究竟是先验的还是经验的,但我觉得黎曼或多或少地认为,空间是一些延展的量,而度量是它们最本性的特征。尤其是黎曼认为,度量不应该是先验的,黎曼几何也缘此成为了广义相对论的基础。出于这样的空间观,他构造了一种“机动又统一”的度量方式并把这种度量方式当作某一恰当的空间上的一个结构,这是黎曼几何的精华所在。
为了理解黎曼几何的精华,请回忆平面上第二类积分曲线的长度用参数形式可以表示为:
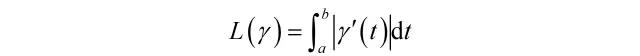
其中|γ’(t)|代表曲线γ上在参数为t处的切向量长度,其度规由欧氏空间诱导,即:
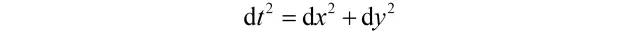
这意味着用同一把尺子去测量曲线γ上每一点的切向量长度。现在考虑一系列刻度彼此不同的尺子,并用这些尺子中的一把去测量曲线γ上一点的切向量,这样我们就用不同的标准为每一点的切向量赋予了长度。很自然地,应该按如下方式组织度规:
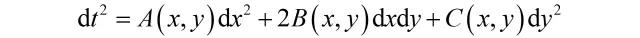
它是dx与dy的二次型*,其中A、B与C是坐标的函数。由此可见,每一点的测量都有各自的标准,但这些标准又最终统一在黎曼度量之下,这就是“机动又统一”的所在。
* 注:二次型是项数最多的二次齐次多项式
显然,适应于这一结构的抽象空间并不能用笛卡尔坐标一揽子地覆盖。以自己的空间观为依据,黎曼提出用一系列相邻相容的局部笛卡尔坐标系来覆盖适应黎曼度量的抽象空间。这一构造被后人总结为:该抽象空间的局部相似于欧氏空间。从这里,相似性的问题又浮出水面。现在人们已经知道,黎曼定义的抽象空间,在局部与欧氏空间拓扑等价。这样一来,空间在局部配有微积分工具,又统一在黎曼度量之下。黎曼几何因此平息了非欧几何的争议,使得拓扑研究在更广阔的背景下继续进行。
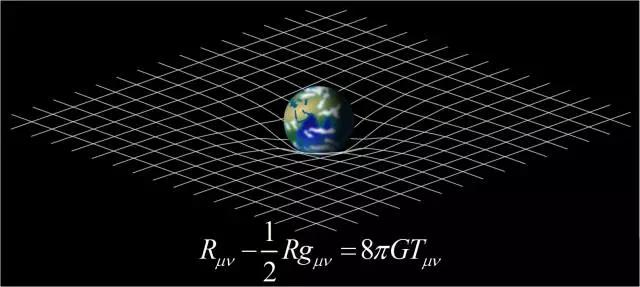
图9:时空弯曲与广义相对论场方程。该方程是二阶非线性偏微分方程,左边是时空度规,右边是质能分布,它表明时空度规受质能分布影响。这就是物体运动与钟慢尺缩效应的最终解释。(图片来自wikipedia.org)
实际上,在黎曼时代,对于欧氏空间与二维曲面上的拓扑结构的研究已经变得明朗,关键的一步是研究对象是否能从欧氏空间与曲面顺利过渡到高维抽象空间,正是黎曼几何帮助拓扑完成了这一过渡。凭借抽象空间与其上度量的构造,黎曼站在了当时拓扑研究的制高点。
五、其他工作
李斯亭除了在1847年发明Topologie一词之外,还于1862年出版了《空间复形的概述》[15]进行相关研究。德国数学家莫比乌斯(August Ferdinand Möbius)与李斯亭在1858年分别独立地发现了不可定向曲面,莫比乌斯带就是一个好例子。意大利数学家贝蒂(Enrico Betti)向高维推广了黎曼连通阶的概念,如今拓扑不变量贝蒂数已经在持续同调的应用领域大放异彩。在《机器证明的历史片段》一文中被提及的四色定理也属于拓扑的范畴,它于1852年被英国数学家格斯里(Francis Guthrie)以猜想的形式提出。2005年,证明机Coq给出了它的形式证明。

图10:莫比乌斯带只有一个面与一条边界。它是一个不可定向的二维紧流形。(图片来自wikipedia.org)
注释:
[1] J.B.Listing, Vorstudien zur Topologie, Vandenhoeck und Ruprecht, Göttingen, p.67, 1848
[2] J.德比希尔,素数之恋:黎曼和数学中最大的未解之谜,第18章,上海科技教育出版社,2014
[3] L.Euler, Solutio problematis ad geometriam situs pertinentis, Comment. acad. sci. Petrop. t. 8, Saint-Petersbourg, 128-140, 1736
[4] L.Euler, Elementa doctrinae solidorum, Novi comment. acad. sc. Petrop., 4, 109-140, 1752-1753
[5] P.J.Federico, Descartes on polyhedra: a study of the De solidorum elementis, Springer, 1982
[6] R.Descartes, Œuvres inédites de Descartes, par le comte Foucher de Careil, A.Durand, t. 2, 1859
[7] M.克莱因,古今数学思想(第四册),第50章,第3节,上海科学技术出版社,1979
[8] C.F.Gauss, Disquisitiones generales circa superficies curvas, Comment. soc. reg. sci. Göttingensis recent. cl. math., vol 6, 99-146, 1827
[9] P.O.Bonnet, Mémoire sur la théorie générale des surfaces. J. de l'École Poly., Tome 19, Cahier 32, 1-146, 1848
[10] T.Hall,高斯:伟大数学家的一生,第3版,田光复译,台湾,凡異出版社,1986
[11] B.Riemann, Grundlagen für eine allge meine Theorie der Functionen einer veranderlichen complexen Grosse, Inauguraldissertation, Göttingen, 1851
[12] B.Riemann, Theorie der Abel'schen Functionen, J. f. Math., 54, 1857
[13] B.Rernhard, Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. In: Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen 13, 133-150, 1868
[14] B.Rernhard, Ein Beitrag zu den Untersuchungen über die Bewegung cines flüssigen gleichartigen Ellipsoides, Abh. d. Königl. Gesell. der Wis. zu Göttingen 9, 168-197, 1861
[15] J.B.Listing, Der Census räumlicher Complexe oder Verallgemeinerung des Euler'schen Satzes von den Polyedern, Abh. d. Königl. Gesell. der Wis. zu Göttingen 10, 97-180, 1862
(未完待续)
参考资料:
[1] 干丹岩.代数拓扑和微分拓扑简史[M]. 湖南教育出版社,2005
[2] 陈克胜.民国时期中国拓扑学史稿[M]. 科学出版社,2014
[3] I.詹姆斯.数学巨匠——从欧拉到冯·诺依曼[M]. 潘澍源,林开亮译.上海科技教育出版社,2016。
[4] M.克莱因.古今数学思想(第三册),上海科学技术出版社,1979
[5] M.克莱因.古今数学思想(第四册),上海科学技术出版社,1979
[6] M.Spivak. A Comprehensive Introduction to Differential Geometry, Vol. 2, 3rd Edition, Publish or Perish, Inc, 1999
声明:文章转自【无穷集】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











