自然界中存在大量的正态分布,比如女性的身高:

图1(图片出自这里)
正态分布的英文名为:Normal Distribution,台湾翻译为常态分布,可见一斑。可是为什么这么常见呢?
每个人都相信它(正态分布):实验工作者认为它是一个数学定理,数学研究者认为他是一个经验公式。
——加布里埃尔·李普曼
一、高尔顿钉板

图2
弗朗西斯·高尔顿爵士(1822-1911),查尔斯·达尔文的表弟,英格兰维多利亚时代的博学家、人类学家、优生学家、热带探险家、地理学家、发明家、气象学家、统计学家、心理学家和遗传学家。
他发明了一个叫做高尔顿钉板的装置,展示了正态分布的产生过程:
视频1
1. 细节
我们来看看高尔顿钉板的细节,或许有助于我们理解正态分布为什么常见。
弹珠往下滚的时候,撞到钉子就会随机选择往左边走,还是往右边走:

图3
一颗弹珠一路滚下来会多次选择方向,最终的分布会接近正态分布:

图4
2. 扯淡
自然界中为什么会有那么多正态分布?下面开始胡诌了。
比如开头提到的女性身高,受到多个因素的影响,比如:
● 父母身高
● 家里面的饮食习惯,比如吃素还是吃荤,吃牛肉还是吃猪肉
● 是否喜欢运动,喜欢什么运动
这些影响,就好像高尔顿钉板中的钉子:

图5
要不对身高产生正面影响,要不对身高产生负面影响,最终让整体女性的身高接近正态分布。
中心极限定理说了,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布,其中有三个要素:
● 独立
● 随机
● 相加
每次采样受到各种随机性的影响,就好像钉板中的钉子,对采样结果进行或者正面、或者负面的影响,最终让结果形成了正态分布。
高尔顿钉板还有两处细节:
● 顶上只有一处开口:这是要求弹珠的起始状态一致。类比女性身高的例子,就是要求至少物种一致,总不能猪和人一起比较。换成数学用语就是要求同分布
● 开口位于顶部中央:这倒无所谓,开在别的位置,分布形态不变,只是平移
二、为什么还有很多不是正态分布?
在医学研究中很多分布就不是正态分布,对实施了前列腺癌症治疗的病人进行前列腺特异性抗原(Prostate specific antigen)的检测,检测结果的分布不是正态分布:
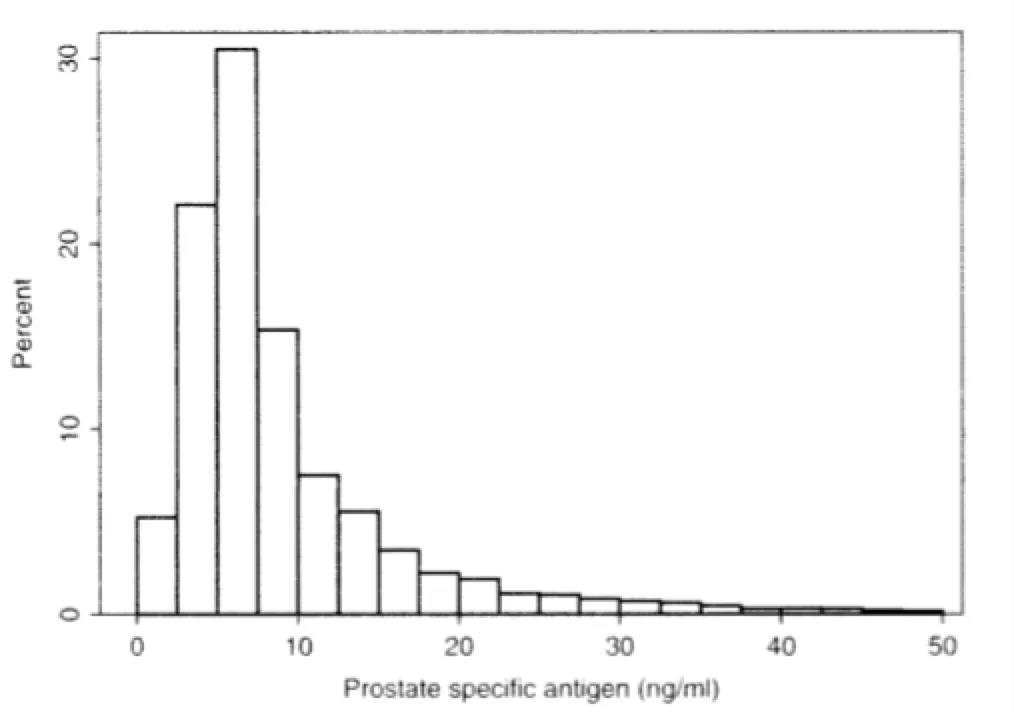
图6
这里可能有两个原因导致了这一现象。
首先,样本取自实施了前列腺癌症治疗的病人,这些病人往往有各种各样的疾病,并不是全体人类样本,也就是说不够随机,所以结果很可能会偏向某一边。
其次,癌症并非是相加,癌细胞的分裂更像是乘法:

图7
数学中,可以通过对数来把乘法变为加法:
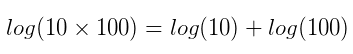
图8
因此我们对之前的数据取自然对数,结果就接近于正态分布了(这就是对数正态分布):
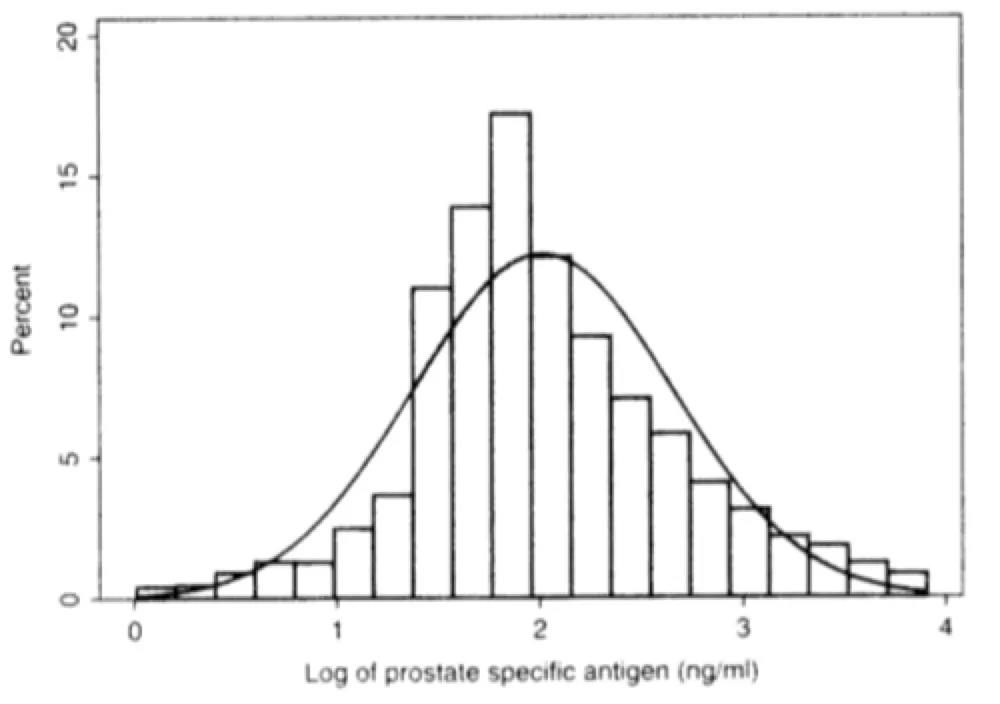
图9
看上去还有点偏向左边,或许是因为采样不是取自全体人类,导致随机性不够。
以上数据及图片来自于《What is a p-value anyway? 34 Stories to Help You Actually Understand Statistics》。
财富分布也是有乘法效应在里面,这就是所谓的“马太效应”:
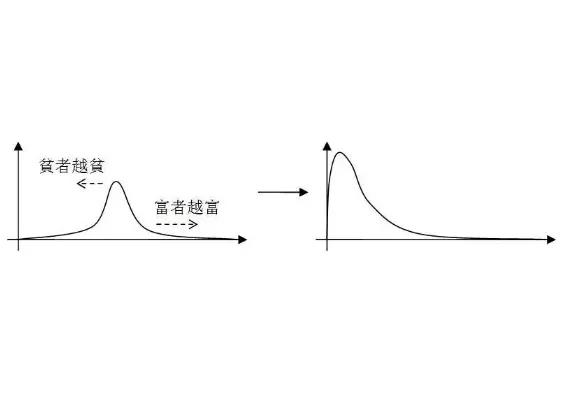
图10
多说几句自己的感想吧,对于财富分布,我们大家肯定都希望自己往横坐标的右侧靠近。
那么在每次碰到钉板中的钉子时,都需要做出往左走还是往右走的选择,所以我们需要努力提高自己,使自己的选择比扔硬币的正确率高,减少随机性,这样才能尽量往右走。
以后回答为什么要学习?“因为正态分布啊!”
声明:文章转自【马同学高等数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











