一、By:王小龙
复数不仅有意义,而且可以用图示来优雅地解释。
1. 实函数与数轴变换
大家都认识y=ex,对于这样的初等函数,我们从小就学会使用直角坐标系来刻画它们:
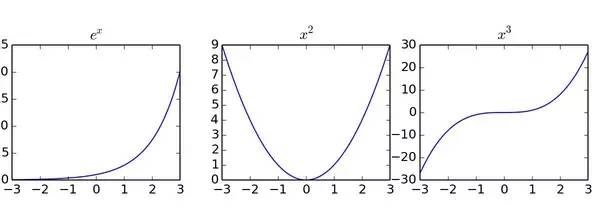
图1
它们的特点都大同小异:把实数轴对应到实数轴。然而,既然是一维函数,用二维图像来描述未免太过奢侈。如果我们把数轴涂上不同颜色,再把一条新数轴上对应的函数值涂上相应颜色,就可以清晰地用数轴-数轴对应来展示函数这一关系:
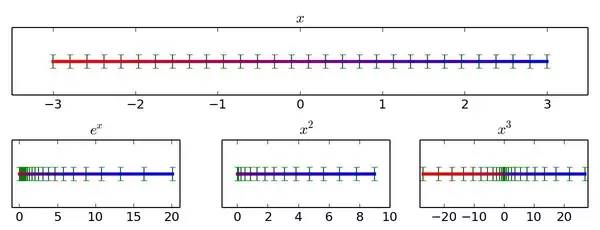
图2
可以发现每个函数的作用无非是在有些地方把数轴往中间压了压,在有些地方又把数轴往两边扯了扯(观察图中小棒棒之间的间距是变窄还是变宽):
● ex越往左越挤压数轴,越往右越拉伸数轴
● x2离0越远,对数轴的拉伸越厉害(在图上左半边图像和右半边图像重叠在了一起)。如果有一个小球在实数轴上向右滑行,那么它的像则先向左滑行到0,然后再向右滑行。
● x3离0越远,对数轴的拉伸比楼上更厉害,但是不同的是,向右滑行的小球的像也一直向右滑行。
是挤压还是拉伸,就看函数在那一点的导数的绝对值是小于1还是大于1。因此导数大小的意义就是局部小区间在变换下的伸缩倍数。导数正负符号的意义是小区间是否反向,比如第二个函数x2在x小于0时导数也小于零,那么指向右方的数轴负数部分经过变换指向了左方。
2. 复数与平面变换
既然可以用上面的数轴—数轴对应来描述一维函数,那么类似地,就可以用平面—平面对应来描述二维函数。我们用一个复数表示平面上的点,用字母i区分纵坐标,就可以来研究复数函数的性质,其中
。假设我们已经默认了复数的运算:
● 加法:
● 乘法:
● 极坐标分解:,其中
是复数代表的平面向量到原点的距离,
是和横轴正方向的夹角。
拿出一个涂色的平面网格(从左上开始逆时针依次涂成红黄蓝绿色),把每个网点的像算出来,按顺序连起来,就可以来研究复函数了。
2.1. 复数的加法:
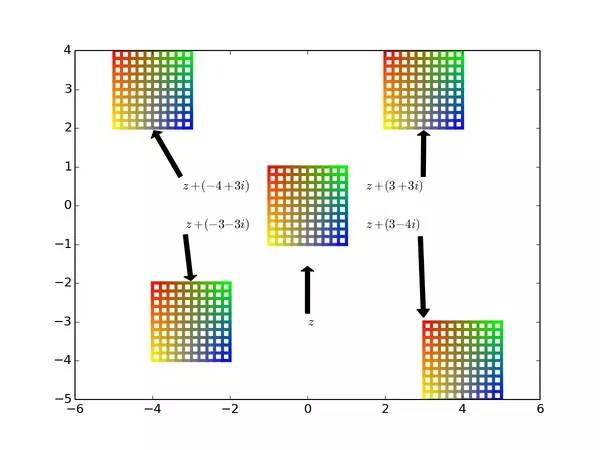
图3
● 从图中可知,加法就是平面的平移,平移量恰好是那个复数对应的平面向量。
2.2 复数的乘法:
根据上面的运算法则很容易得到函数的二维对应关系是
,画在图上就是:
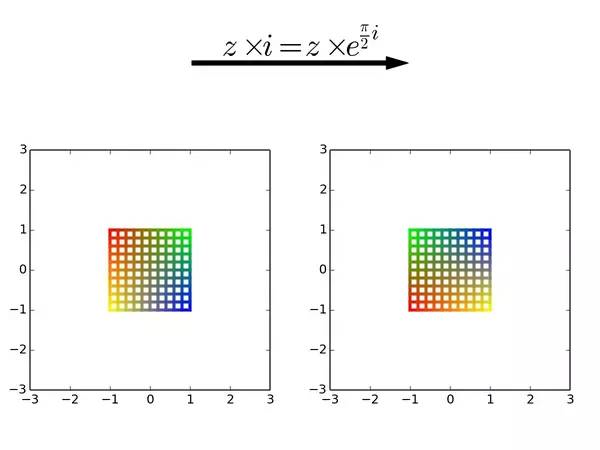
图4
● 仔细看可以发现,各点乘以的效果是平面逆时针旋转了90度,也就是
弧度。
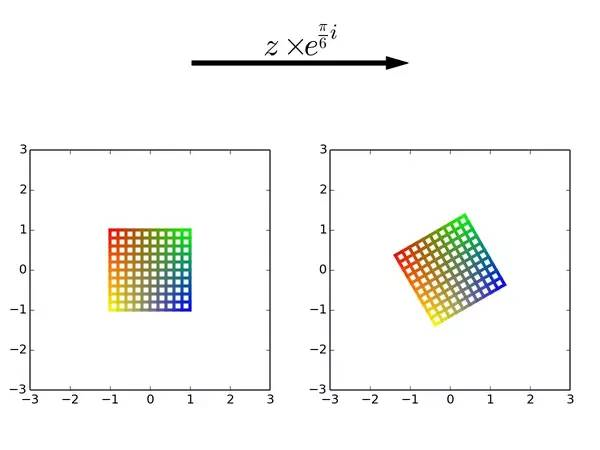
图5
● 各点乘以的后果是平面逆时针旋转
弧度,这里是30度。
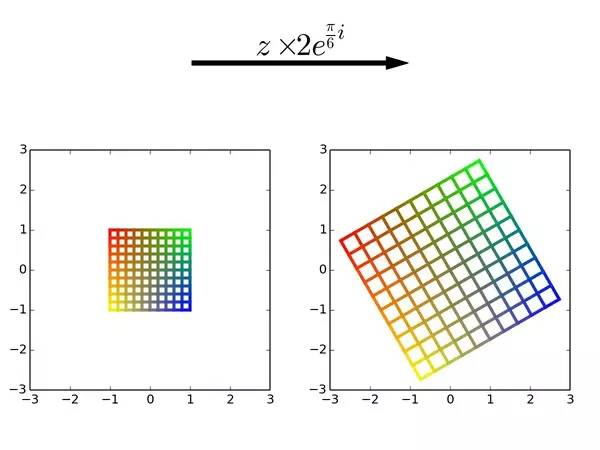
图6
● 乘以一个一般的复数,就是把整个平面按它对应的角度旋转弧度,再均匀放大
倍。
因此,复数的加法就是自变量对应的平面整体平移,复数的乘法就是平面整体旋转和伸缩,旋转量和放大缩小量恰好是这个复数对应向量的夹角和长度。二维平移和缩放是一维左右平移伸缩的扩展,旋转是一个至少要二维才能明显的特征,限制在一维上,只剩下旋转0度或者旋转180度,对应于一维导数正负值(小线段是否反向)。
3. 复变函数与伸缩旋转
如果在每一个点处的旋转、放缩和平移量都不同(导数不同),就可以得到比较复杂的复数函数,举个例子:
3.1.
,从上一小节的知识可知,
的作用就是把平面上每个点按自己对应的坐标放大
倍、旋转
弧度。我们立即可以猜测这个函数在x较大的地方放大的倍数更多,因为放大率
更大;在x轴上只伸缩不旋转,因为没有
旋转分量;在y轴上只旋转不伸缩,因为没有
放缩分量:

图7
● 请看左图中的横向中轴,它在右图中的像也是横向中轴,只不过左边压缩,右边扩展,这正是我们一开始就提到的一维指数函数。而这个图,恰好就是一开始那个数轴-数轴对应朝两边扩展形成平面-平面对应的结果。
● 再请看左图中的竖直中轴,它在右图发生了弯曲,贴在了单位圆周上,因此变成了一系列纯旋转的复数乘子。这一点在一维中可完全没有类似物,请谨慎类比。
● 其他点介于纯粹旋转和纯缩放之间。最后,请你回过头再仔细看看这幅图,你会发现这几段话也适用于图中的每个小正方形。小正方形变换前后的旋转和伸缩比例对应于函数的导数,本例中函数的导数就是原函数自己。
3.2.
● 加10就是整体向右平移10个单位,可以最后再看。
● 咱们来看,令
,可以得到:
,这说明单位圆以内(
)函数压缩,单位圆以外(
)函数拉伸,离原点越远拉伸越厉害,正方形网格应该越来越大。
● 原正方形的四个彩色顶点的角度是135、225、315和45度,分别乘以3再取余360到[0,360]度之间变成45、315、225、135。因此正方形的像从左上逆时针看颜色从红黄蓝绿变成了绿蓝黄红。
图像也和上面的分析完全吻合:
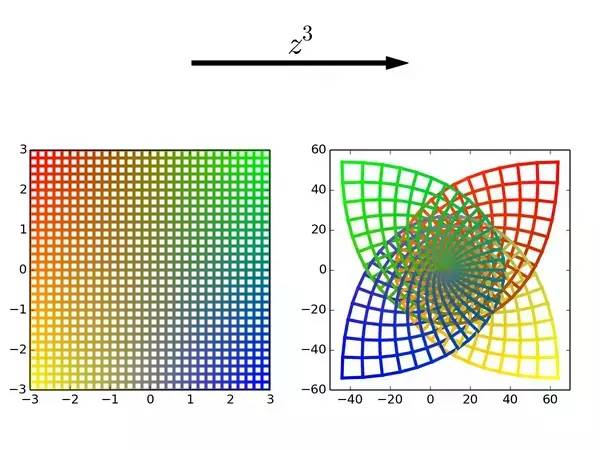
图8
举上面两个例子是想向大家展示伸缩和旋转是优雅地解释复数的有力工具。
4. 复变函数和小正方形
接着我们随便看几个复数函数对应的平面变换图像:
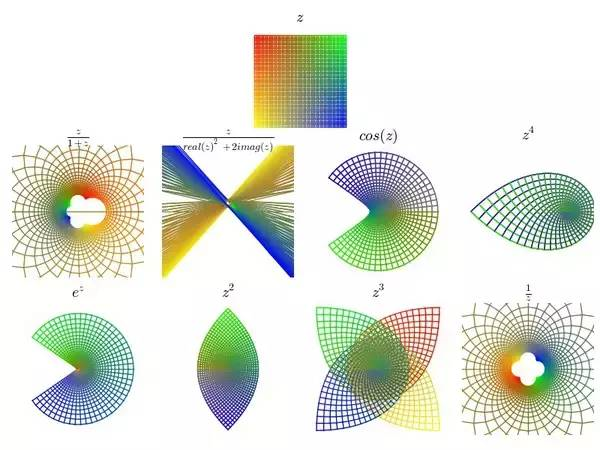
图9
漂亮吧,但是且慢!为什么第二个函数图像比较丑?因为二维函数很复杂,有一小类二维函数的变量之间具有一定关系,导致的结果是虽然整体变换多姿多彩,但是如果只观察局部,这些函数一定把足够小的小正方形变成小正方形,不会压扁它或拆散它,只不过平面不同地方小正方形放缩和旋转程度不同。第二个函数就不属于这种特殊的函数类。
这种性质很好,图像很美的函数称为解析函数,它的变量之间的联系称为柯西黎曼方程,局部小正方形的放缩和旋转幅度恰好等于这个复函数在那一点的导数值(和第一段一维函数的原理极其类似,在那里一维导数用来刻画伸缩和左右方向)。简单的一维函数,可以唯一地向两边扩展成为对应的复解析函数。
如果把初始的正方形网格用极坐标进行参数化,解析函数仍然把小正方形变换为小正方形,与上图对应的图像为:
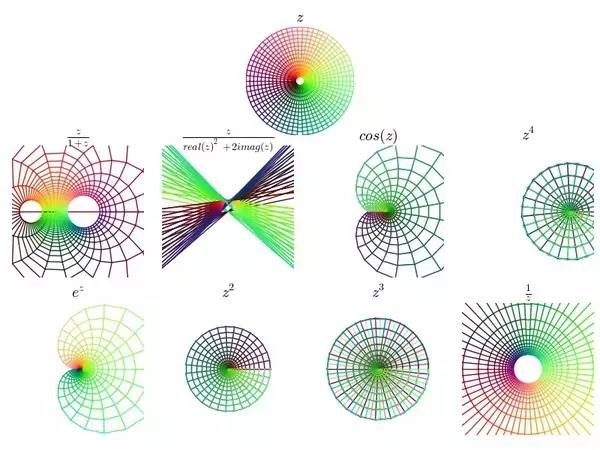
图10
以后看到复变(准确地说是解析)函数,可要记得它们的本质是对平面局部做旋转和缩放,但保持小正方形形状不变。而一个复数就是一个能把平面进行均匀缩放和旋转的乘子。最后,请记得我的彩色正方形!
二、By:Heinrich
复数最直观的理解就是旋转!
4*i*i = -4
就是“4”在数轴上旋转了180度。
那么4*i就是旋转了90度。
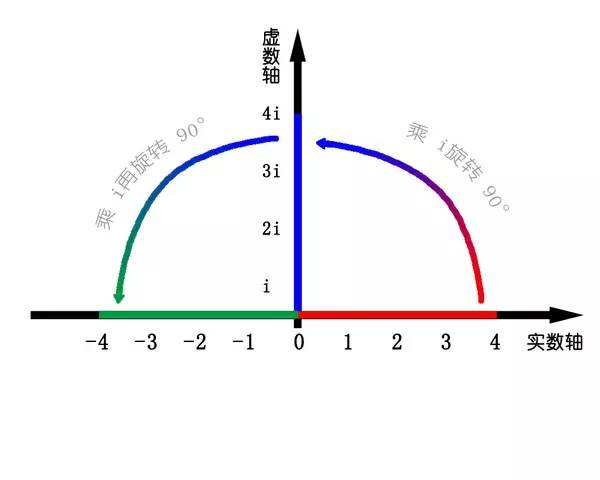
图11
另外,et 是什么样呢?
图12
但当你在指数上加上i之后呢?
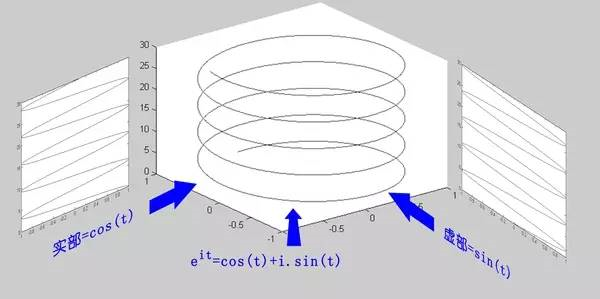
图13
变成了一个螺旋线。是不是和电磁场很像?(想拿欧拉公式去跟女生炫学术的男生注意了:她们,真的,不CARE)
当然,更重要的意义在于复数运算保留了二维信息。
假如我让你计算3+5,虽然你可以轻松的计算出8,但是如果让你分解8你会有无数种分解的方法,3和5原始在各自维度上的信息被覆盖了。
但是计算3+5i的话,你依然可以分解出实部和虚部,就像上图那样。
基于以上两个理由,用复数来描述电场与磁场简直完美到爆棚!
我们即可以让电场强度与复数磁场强度相加而不损失各自的信息,又满足了电场与磁场90度垂直的要求。另外,一旦我们需要让任何一个场旋转90度,只要乘一个“i”就可以了
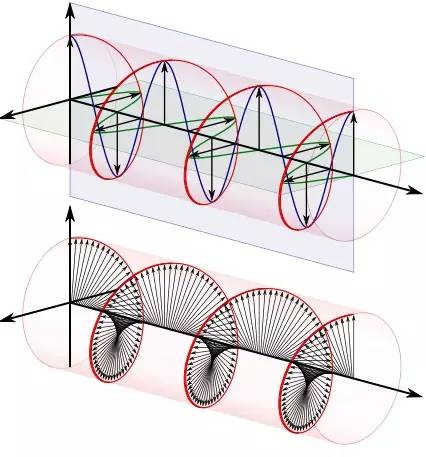
图14
受 @physixfan 答案的提醒,再补充一点。
正弦波在频域可以看作是自然数中的“1”,可以构成其他数字的基础元素。当你需要5的时候,你可以看成是1*5(基础元素的五倍)也看以看成2+3(一个基础元素2倍与基础元素3倍的和)。这些用基础元素构成新元素的运算是线性运算。
但是现在你如何用线性运算吧2sin(wt)变换成4sin(wt+pi/6)呢?
利用欧拉公式,我们可以将任何一个正弦波看作其在实轴上的投影。假如两个不同的正弦波,可以用数学表达为:
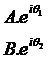
好了,现在如果我想用第一个正弦波利用线性变换为第二个,我们就只需要将A乘对应的系数使其放大至B(本例为乘2),然后将θ1加上一定的角度使其变为θ2(本例为加30度),然后将得到的第二个虚数重新投影回实轴,就完成了在实数中完全无法做到的变换。
这种利用复指数来计算正弦波的方法也对电磁波极其适用,因为电磁波都是正弦波,当我们需要一个电磁波在时间上延迟/提前,或是在空间上前移/后移,只需要乘一个复指数就可以完成对相位的调整了。
三、By:Octolet
不少学物理的人都觉得“物理意义”是一个没有良定义的概念,而且由于这个词在民科之中极高的出场率,导致大家对这个词都很反感。但是,这并不代表我们不能为复数在物理中的大量应用找到一个合理的,足够“物理”的解释.
引入复数的一个很“物理”的原因是因为对称性。
大家最早在物理中接触复数,基本都是在简谐振动那部分。简谐振动的动力学方程是:
这个方程,其实蕴含着SO(2)对称性。
为了看出这一点,先注意到,这个方程是一个二阶线性齐次方程,在知道其初值条件之后就能求解初值问题,得到轨迹
。考虑
和
之间的关系,可以定义一个算符
,这个算符作用在
时的初始条件
上可以得到
时的位移和速度
。
显然,满足的最简单的一个关系就是:
。 同时,由于
这个方程满足时间平移对称性,所以我们有:
。因此
满足的关系实际上是
。
我们都知道,方程的解有周期性,也就是说
还满足
。对于
,
说明
是个交换群,
说明
同构于SO(2),也就是所谓的旋转群。不仅如此,由于方程
是齐次线性方程,所以
其实是
上的2维线性空间
上的线性变换。
到了这一步,我们可以知道为什么要引入复数了。因为首先复数本身可以看成上的2维线性空间,并且SO(2)在复数域这个
上的2维线性空间上有一个自然的表示:
在复数乘法下自然构成了一个同构于SO(2)的群。所以用复数我们可以方便地表示简谐振动的解。这件事严格来说是这样做的:
1. 首先,作为一个
上的2维的线性空间,跟
上的二维线性空间
是同构的。我们有同构映射
以及
。
2. 其次,同构于
,有同构映射
。 有
。 我们希望
是由
“生成”的,也就是说
。我们可以取
3. 对于一个初始条件,有
。
4. 对于,
5. 所以,我们可以写出简谐振动的解,为:以及
。
这就是好几个高票答案所谓的“复数表示旋转”的一个本质原因。
量子力学里引入复数,虽然说历史上似乎是因为量子力学跟波动方程的关系引入的,但是本质的原因不太一样。从对称性的角度上来说,经典量子力学里的对称性是Unitary对称性,相应对称群是U(n)。而最简单的情形U(1)群跟SO(2)恰好有很紧密的联系,在复数上表示也很方便。
从物理的角度看,用复数表示还是用矩阵表示其实不重要,重要的是代数结构,或者说描述对称性的对称群在什么代数结构上表示比较方便。所以,真正的问题不是“复数对于物理有什么意义”,而是“复数域这个代数结构对物理有什么意义”,这样的代数结构包含了怎样的对称性?
但是这个问题其实也还没有回答完。物理中其实有着更复杂的对称群,为什么人们“止步”于复数域(就是说更复杂的对称群一般考虑在上的线性空间上的表示)呢?
其实,还真的有引入比复数域更复杂的代数结构来研究比SO(2)更复杂的对称性问题的例子,比如著名的四元数,可以用来研究三维旋转问题(SO(3)群的表示)。但是,这些比复数域更复杂的代数结构一般来说其性质远没有复数域那么好,比如四元数虽然是个除环,但是不是域,乘法不可交换。
这就说明了为什么物理中要引入复数域,并且“止步”于复数域。复数域上一些基本的对称群有自然的表示,并且复数域的代数性质和分析性质都非常非常好,所以物理学很自然地需要这个代数结构。
四、By:Yike
我将试着用通俗易懂的方式解释复数的意义——不喜欢太多公式和专业术语的各位有福了。
---------------------狂妄自大的分割线--------------------
开始
我们的世界中存在着各种各样的波。
声音是波,光线是波,冲击岩石的海浪是波,街霸里面RYU和Ken都能发冲击波……
这些波,除了冲击波之外,存在形式都是正弦的。
正弦函数是自然之中一种优美的存在。
另外一方面,我们所处的这个世界充满了信号。我们使用信号传递信息。
语言是信息载体,音乐是信息载体,光线是信息载体,颜色是信息载体。
但是任何不会发生变化的信息载体,比如,持续保持的一片白光,或者是持续不变的1kHz声音,是不能传递信息的。
或者应该说得更正确些,信号的能传递的信息的容量,跟信号的变化速度,也就是频率,有非常大的关系。(变化的)频率越高的信号,能传递的信息量可以越高。
变化的信号,显然是不能用一个单调的正弦波来描述的。
但是,牛B的前人发现,任何一个信号,不管它有任何的形状,随着时间会如何变化,我们都可以用一堆不同频率和幅度的正弦波叠加,复现出来。
这里我们要记住一个结论:
我们可以通过把一个信号变成是不同频率的正弦波信号的叠加,从而在频域分析信号。
然后我们通过分析一个系统对不同频率的信号的不同响应,就可以分析系统的信号响应。
好像有点儿绕……
我看见大家迷惘的眼神了: 不是说好是来说复数的吗,怎么讲到信号和正弦波上去了。
嘿嘿,不要着急。
描述正弦波,有两个重要的指标:幅度和相位。
打个比方,你如果告诉我,在某一个时刻,有一个正弦信号在一个节点上,它的幅度是1V。
那么我是没有办法知道在这一时刻,这个节点上的电压的绝对值是多少的。
想要知道这一时刻电压的绝对值,就必须要知道这一时刻这个正弦信号的相位是什么。
另外一个问题是,一个正弦信号在传播的过程中,在通过某个系统以后,它的幅度和相位都有可能发生改变。
这下研究信号的工程师犯难了:
我得想个办法,同时描述相位和振幅,这样才能更有效地用公式来描述一个信号,或者用公式来描述一个系统对信号的响应。 哎呀,难煞我也。
好了,现在轮到复数出场了。
虚数和实数,在复平面上时两根轴。而一个复数,会同时包含了实数信息和虚数信息,这样,它就变成了平面上的一个点。
很有意思,这个点到平面原点的距离,就恰好能描述一个信号的振幅,而这个点到原点连线以后跟实轴所成的角度呢,恰好能够描述信号的相位。
于是复数的物理意义在于:
给物理学家一个机会,去优雅地处理正弦信号。简洁地同时描述幅度和相位的变化。
由于正弦信号在物理的世界里无处不在。复数不能简单地对应一种物理量。
但是它可以参与描述所有和正弦信号有关的物理量。
以上算是回答完了题主的问题。
以下是实际例子部分,来让大家理解得更透彻。
现在假设有幅度为1V,相位为0度的信号,要通过一个系统,得到一个电流。
简单起见,我们首先假设这个系统就是一个电阻。
那么这个系统对信号的处理是怎么样的呢? 就是1/R对不对?(注意这里没有虚数,不需要虚数的原因很简单,因为电阻是没有记忆的器件,它对电压的反应是立刻,实时的,没有相移。0相移就意味着这个复数可以用一个实数来表达)
后来,有好事者,把电阻换成了一个电容。
这个系统对直流电压的响应是0,直流电压加在电容上,是不会有电流通过的。
但是对于一个有频率的电压信号来说,就是另外一回事情了。
我们知道电流的公式是
所以流过电容的电流也是一个正弦信号,它的幅度是
(注意这一幅度不是一个恒定值,在不同输入电压频率下,有不同的值。这就是“频率响应”的概念)
但是要注意它的相位跟输入的正弦电压信号不!一!样!
恰好是九十度的相移,因此我们恰好可以用虚数 i 来描述这一相移。
所以只有一个电容的系统,对信号的响应是:
其中的负号表明系统的相移在-90度。
看见虚数了吧??!!
很优雅地,就用一个复数同时表明了一个正弦电压信号流过一个电容得到一个电流,它的振幅变化是多少,它的相位变化是多少。
有了这一工具,我们就能开始去分析复杂的系统对信号的响应。这样我们才能有效地去构建和分析有反馈的系统。
有了反馈系统,我们的运放这种牛玩意儿的存在才有价值。
而运放本身,也是有频率响应的。它的最基本的波特图分析,其基础也是信号与系统。而信号与系统的知识网络构建,就离不开复数的参与。
五、By:Riinn
复数只是一种表示,你完全可以采用同构的东西来取代它,比如很多人提到的
所以,复数本身没有任何物理意义。当然,如果精确到同构的话有一些物理上的概念需要用复数这个结构来表示,不过我学的不多就不说这些了。
说实话,我觉得一个非物理概念具有物理意义是一件很奇怪的事情。不过,如果说到复分析的话还是有一些和物理有关的东西可以讲的。
但是,我们仍然可以用物理中的东西来理解复分析。这里就不再谈什么复函数在局部相当于伸扭什么的几何性质了,几何意义和物理意义不是一个东西。
复函数和向量场有着很大的关系。
首先,全纯函数的实部和虚部都是调和函数,并且它们的等值线正交。于是一个全纯函数的实部与虚部分别给出了满足一定边界条件的静电场的场线和等势面。当然,也可以用复函数来获得一些其他的二维 Laplace 方程的解(比如导体板上的电流分布、热流分布、平面不可压缩流体等问题)。
这看起来有点巧合,下面是复函数与向量场看起来不那么刻意的联系。
我们通常用两个复平面之间的变换来表达一个(单值的)复函数,这里采用一种新的表示方法:把每一点赋予一个复数
的向量表示,这样,一个复函数就可以用一个平面向量场来直观表示出来了(Polya 向量场)。
可以证明,在这种表示下这个场的散度与旋度同时为零当且仅当这个复函数是全纯的。另外,环路积分的实部与虚部分别是这个环路的旋度与散度。
(按照上面的方法)幂函数对应的向量场和电偶极子的场线是一样的,
则类似于四极子。常数场
在球极投影之后看又是一个无穷远点的偶极子,
则是四极子。其他的幂函数以此类推。这样,洛朗级数,就可以看成是无穷个偶极子的叠加。你在有限远出往原点走,就能看到局部形态慢慢变成偶极子的形状再变成四极子的情况,往无穷远点处走也是类似的。
至于留数定理,就是说只有给出的偶极子在环路积分下不消失,这样,一个环路积分唯一的效果就是它对各个极点、奇点处展开中偶极子的作用效果。
(待续……)
另外,复射影几何与量子力学有关。
一个量子态通常是被归一化的,
,并且可以乘上一个全局相位因子不影响其物理意义。这样,我们也可以理解成量子态是把所有的
压缩到一个等价类里面后的结果。这样的话我们就得到了复射影几何。
我们知道莫比乌斯变换在复分析中起到了重要的作用(比如它刻画了单位圆盘上的全纯自同构群),它看起来很不自然,不过它其实是射影几何中的基本变换。
二维情况下,采用球极投影,我们可以把扩充复平面与黎曼球面等价起来,而这个球面就是量子信息中的 Bloch 球。在量子力学里面重要的酉变换可以被视为是一个莫比乌斯变换的子群,这一类变换在黎曼球面上的作用效果是球面上的旋转,也就是通常说的对一个 qubit 的量子门作用总是 Bloch 球面上的一个旋转。
假如引入复数的推广——四元数的话,我们可以看到四元数分别就是 Pauli 矩阵
,利用这些东西可以方便地表示 Bloch 球上的任意旋转。
来源:知乎
声明:文章转自【算法与数学之美】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











