说起几何元素,很多人都会觉得这太枯燥乏味。是的,学生时代对数学的恐惧令人难以忘怀,然而当你从另一个角度——游戏——去观察几何甚至数学时,你会发现大有不同,《纪念碑谷》就是一个很好的例子。
你可以从《纪念碑谷》中看到很多美妙的几何图形,会让你发现原来富有规则的线条也是那么的令人着迷。
《纪念碑谷2》的开场,和1代完全一样:一个看似S形的立体结构,旋转一下就突然变成了W形,让主人公得以顺利抵达目的地。
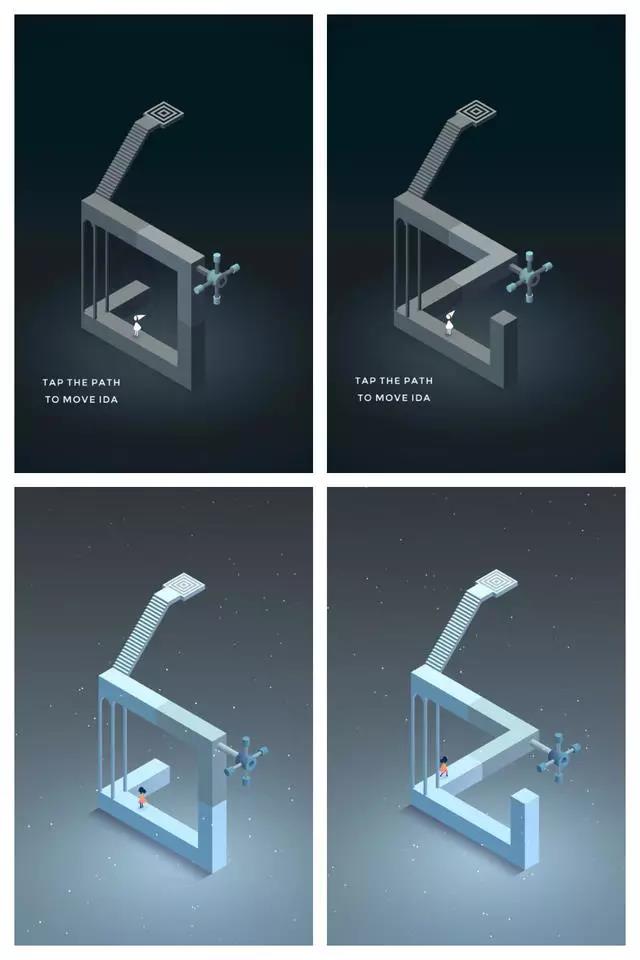
图1:《纪念碑谷》与《纪念碑谷2》游戏第一章对比。(图片截取自游戏)
这个作为教学关的谜题极为简单,恐怕大部分人都不会多看它两眼。但是恰恰是这个简单的开头里,隐藏了《纪念碑谷》全部谜题的核心。
让我们添加几条辅助线:
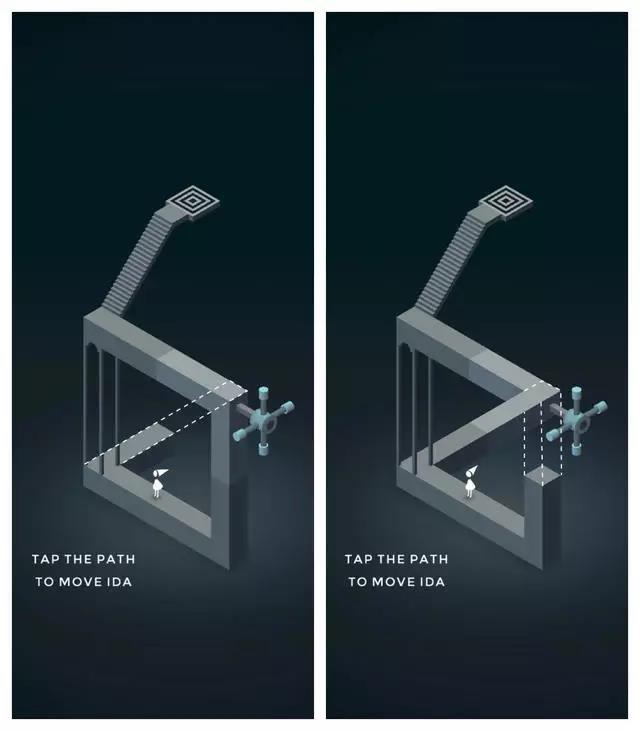
图2
可以看到,它本质上就是这样一个图案:

图3:彭罗斯三角(图片来自网络)
它被称为彭罗斯三角,是所有不可能图形中最基础、最著名的一个。
彭罗斯三角被很多人独立发现过,最早的也许是1934年18岁的瑞典学生奥斯卡·路特斯瓦德的课堂涂鸦(后来他成为了著名艺术家)。但是论得名,还是得归于1956年数学家罗杰·彭罗斯。在看到了M.C.埃舍尔的作品《楼梯房间》(1951)之后,他和他的父亲一起写了一篇论文,分析了这种视错觉,提炼出彭罗斯三角和彭罗斯楼梯等几个基本形态,还把这篇论文寄回给了埃舍尔:
反过来埃舍尔受此启发创作出了最有名的不可能作品:《瀑布》(1961)。

图4:埃舍尔《瀑布》(Waterfall,1961)(图片来源:http://www.mcescher.com/)
这个瀑布的本质就是两个彭罗斯三角叠加,它也被制作者偷偷藏在了《纪念碑谷2》里面。

图5:彭罗斯双三角与《纪念碑谷2》中第十一章场景对比。
一、一个无法解决的矛盾
几十年来数学家、心理学家和艺术家创造出了数不清的视错觉现象,但是不可能图形始终在里面独树一帜。大脑在正常情况下会想方设法消灭矛盾,可面对它的时候,却似乎放弃了治疗。
我们熟悉的视错觉很多是这样的:

图6:裙子是蓝黑还是白金?
对,这就是著名的白金蓝黑裙子问题。有些人看成白金,有些人看成蓝黑,双方各执己见不肯退让。虽然经过努力或者外界帮助,你也可以改变自己的观点,但是你不会一半白金一半蓝黑,不会自相矛盾。
彭罗斯三角就不一样了。不管怎么看,它都是矛盾的、不可能的。
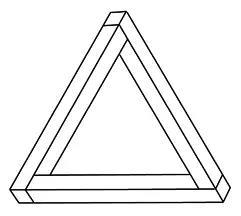
图7:彭罗斯三角(图片来自网络)
这个矛盾的本质说来简单:因为它发生在不同的层级上。分开来看,三角形的三个角,每一个都完全正常,毫无问题:
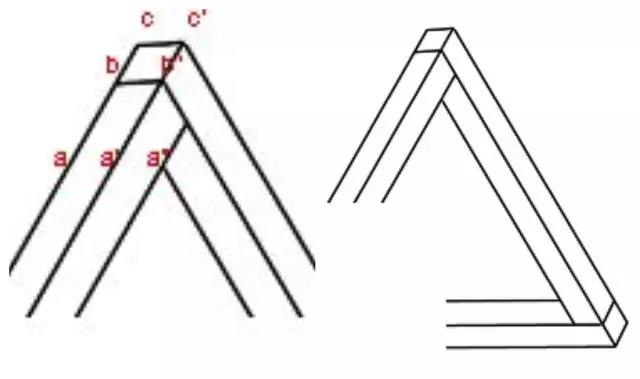
图8
只有当合起来的时候我们才会意识到,这个图形在三维空间里是无法成立的。这一矛盾发生在局部和整体两个层级之间,也正因此我们难以直观地感受到这个矛盾并拒绝它。
但其实消除这个矛盾明明很简单。只要我们把它看成一个平面图形,是三个不对称空心V形拼接而成,一切就迎刃而解。毕竟,它本来就是纸上或者屏幕上的一个平面图形啊!
不行。意志力稍微放松一点,它就会掉回去又变成一个自相矛盾的立体。我们似乎就是有一种把二维线条看成三维物体的冲动,哪怕它会带来矛盾也不在乎。
二、三维幻象
格式塔心理学提出过一个“俭省原则”:当我们看到一个形状的时候,我们会尽量用“最简单”的方式来理解它。比如这样的一个图,几乎所有人都会认为这是三个圆和两个三角形堆在一起,而不是认为这是三条折线和三个奇怪的扇形:
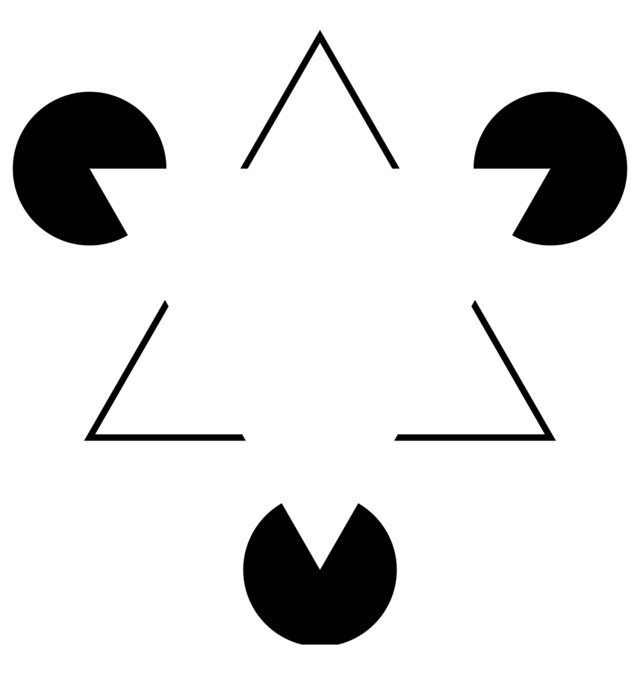
图9
这个现象在三维的时候更加明显,只要有办法能把复杂二维图像理解为单一的三维实体,我们几乎肯定会扑过去,哪怕这个三维物体根本就讲不通:
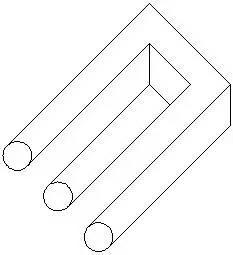
图10:不可能图形:魔鬼叉
这个现象其实倒也不难理解。毕竟,自然界里一切都是三维的,罕有纯平面的图形;但是任何东西在视网膜上的成像都是二维。演化史让我们早就习惯了从二维图像里读出三维的能力,甚至形成了一套约定俗称的“三维信号”;而那些伟大的不可能作品,都充分利用了这些信号。
但是《纪念碑谷》的设计和埃舍尔又有一点不同。在这里,大部分的不可能图形不是静态,而是动态展示的。
三、运动中的不可能
彭罗斯三角的不可能属性来自空间上的并列:每一个拐角都是正常的,合在一起就产生了矛盾。《纪念碑谷》的关卡却把它改变成了时间序列:谜题本身经常没有矛盾,矛盾产生在谜题的两种状态之间。
譬如开场的彭罗斯三角谜题中,两个不同状态下的几何体都是可能的,是切换的行为让它成为不可能——这使得《纪念碑谷》的视觉和埃舍尔的作品之间有了明显的差异。
埃舍尔的许多作品用明确的标记来强化矛盾感。在《瀑布》里,远处的瀑布水道比较狭窄,砖比较小,两侧并不平行,这都是在用透视法指明距离,让观者感受到渠中的水流逐渐流向远方,却突然下落到原点。这些绘画传统里标准的视觉信号,在《纪念碑谷》里并没有出现。

图11:埃舍尔《瀑布》(Waterfall,1961)(图片来源:http://www.mcescher.com/)
相反,《纪念碑谷》沿用的是游戏传统的等角投影:在这个投影下,三个坐标轴的比例尺相同,两两之间都是120度,完全对称。因为这种对称性,远处的物体并不会更小,所以矛盾感的主要来源也随之消失。这样的结果是,《纪念碑谷》中的关键不可能属性往往并不来自静态图像本身,而是在运动过程中“突然”出现的。
典型例子如这一关里的米黄色滑块的两种状态:
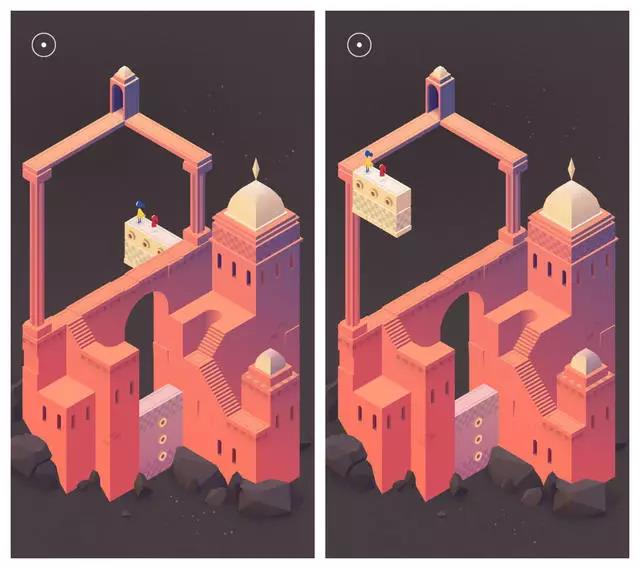
图12:《纪念碑谷2》中第三张场景(图片截取自游戏)
这两种状态单独出现,都不构成矛盾。但是一旦把它们连接起来,就能看到这个滑块的轨迹构成了上下两个不可能图形。这使得矛盾感集中在了滑动的一瞬间。
此外,《纪念碑谷》也在次要环节保留了一部分静态不可能。虽然没有透视法,但依然可以使用遮挡和阴影来实现矛盾,类似于埃舍尔的作品《瞭望台》。《瞭望台》中一个人物手持的不可能立方体,便是这种矛盾最好的案例。

图13:埃舍尔1958年的作品《瞭望台》与《纪念碑谷2》中第五章最后场景的对比。
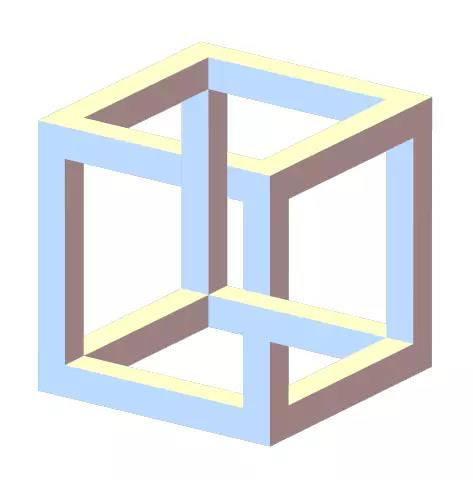
图14:不可能立方体
但也许最为重要的,还是《纪念碑谷》的主角。1代的故事十分简单而抽象,2代为之明确赋予了许多寓意,不过归根结底,最重要的并不是附加的寓意,而是旅程本身。由于每一关的目的无非是从起点抵达终点,这就在关卡中产生了一条无形的线,把所有最重要的不可能属性串连了起来。充满矛盾的旅程而依然连续,这种“元矛盾”的感受,才是这个系列最大的魅力。
声明:文章转自【果壳网】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











