前天我给大家分享了文章《在数的世界里，为什么要从自然数扩大到实数，进而扩大到复数？》，这是选自《数学与生活（修订版）》中的一个章节（标题是我另加的），它的作者是日本当代著名数学教育家，日本数学教育改革先驱远山启，该书以内容适当、通俗易懂的特色而深受读者欢迎，历久不衰，是一本非常不错的数学通俗读物。
在这篇文章中，作者从对四则运算闭合的原则出发，展现了从自然数扩大到实数，进而扩大到复数的思维历程。文章最后提到，在实数范围内，对于四则运算的逆运算“解代数方程”来说，不是闭合的，要想自由地解代数方程，就必须打破实数的框框，导入新的数，这个新的数就是虚数。很多童鞋看到这里意犹未尽，下面我们就来讲讲如何打破实数的框框，引入新的虚数。
首先我们从解二次方程讲起，考虑下面这样的二次方程：
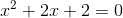
要解这个方程，可以变换成下面的形式：
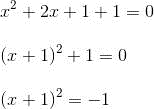
到了这一步就走不通了，因为只要 x 是实数，x+1 也是实数。因此，(x+1)2 就不会是负的，可是它却等于-1。
据远山启在他的著作《数学与生活》中描述，日本德川时代的数学家对于方程有两个根这样的事实是无法接受的，他们把这样的方程起名为“颠三倒四”，意思就是说这是“精神病方程”，那么，像(x+1)2=-1 这样的方程我想他们一定会大骂它是更厉害的“疯狂方程”了。
面对这样的事实，有两种态度。一种是始终抱住实数的框框不放，断定这个方程没有根；另一种是打破实数的框框，把它看作是新的数而主张“有根”。我们无法判断哪一方正确哪一方错误，但是数学的发展是沿着后者进行的。
二次方程有时有两个根，有时一个根也没有，这个事实对于讨厌例外的数学家来说，是不能不想的。要是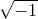
存在的话，那就一切都如意啦。这种无法摒弃的念头，在很长时期支配着数学家。
在引进了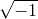
这后，所有的二次方程都有解了。比如对于前面的对于二次方程
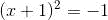
如果不管等式右边的负，加以开方的话，就有
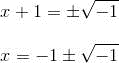
但是数学家们对解释负数的平方根这样表达式的确切意义感到困惑不安，怀着迷信的敬畏感来看待它们，并将它命名为“虚数”。虚数的英文为 imaginary number，意为想象中的数。直到十九世纪初，当这些数的重要性在许多数学分支中已变得明显时，复数运算有了一个简单的几何解释，这消除了人们对复数的合理性的长期疑虑。
下面我们就来给大家讲讲数复数的几何解释。
我们用 imaginary 的首字母 i 来表示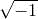
，即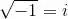
，然后再来探索 i 的性质。
我们知道 i 不是实数，因此可以确定它不在表示实数的直线上，如图所示。
图1
它一定位于这条直线以外，那么它在哪儿呢？
为了找到它，我们回顾一下实数中乘以(－1)的作法。
(＋1)×(－1)=－1
(－1)×(－1)=＋1
(＋2)×(－1)=－2
(－2)×(－1)=＋2
…
总之，×(－1)的作法相当于把实数的直线转绕着原点O旋转了180º。
图2
可是由于 -1=i2，×(-1) 即 ×i2 与 ×i×i 是同样的意义的。如果×i×i与旋转180º相等的话，那么×i 就是旋转180º的一半，也就意味着旋转90º。
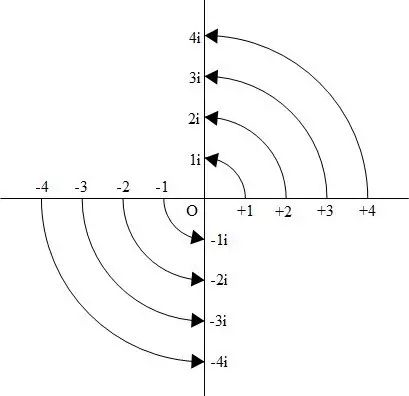
图3
所以×i，水平的实数直线就变成垂直的了。
说穿了，i 这个数位于通过O的垂线上，距离为 1 的地方。
这个垂线上的点全都是2i，3i，…，-2i，-3i，…那样的实数×i 的形式。这样的数叫做纯虚数。
可是仅仅把实数加上纯虚数还不能找出所有二次方程的根。例如：
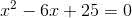
它的根是 x=3±4i，3是实数，而 4i 是纯虚数，根是这些数的和。把这写成式子就是以下的形式：
实数+实数×i
这种形式的数叫做复数。
这种数在平面上的什么地方呢？3还是像原来那样在水平线上，4i 是在与之垂直的方向上移动了4个单位的地方。总而言之，+3就意味着向右移动。+4i 就意味着向上移动。
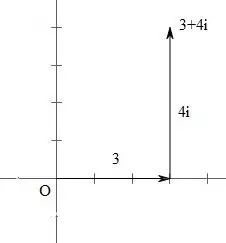
图4
另外一个 3-4i 是向下移动的，所以这个点如下图所示。也就是说复数可以用平面上所有点来表示。
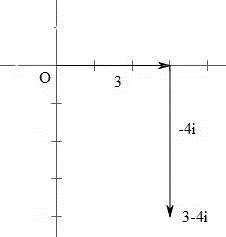
图5
总结一下，复数的几何解释就是把复数 z=x+yi 简单地用平面上带有直角坐标x，y的点来代表。z 的实部就是它的 x 坐标，虚部就是它的 y 坐标。因而在复数和平面直角坐标系上的点之间确立了一个对应，就像数轴上的点和实数之间建立的对应一样。
最先想起用平面上的点来表示复数的是挪威的测量工程师韦塞尔(1745-1818)，但是他的论文在100年左右的时间内被人们忘却了，而另一个发现者高斯却出了名。
参考文献：
[1]《数学与生活（修订版）》，[日]远山启著，人民邮电出版社。
[2]《什么是数学（增订版）》，[美]R.柯朗，H.罗宾著，复旦大学出版社。
声明：文章转自【好玩的数学】微信公众号，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。
