在北美洲的森林里,栖息着一种生命周期十分古怪的蝉类。这些蝉藏于地下长达17年,其间甚少活动,只是吸吮树木的根茎以获得养分。而在第17个年头的五月份,这些蝉只会集体钻出地面,侵入森林,而侵入每英亩(1英亩约为6.07亩)森林的蝉只数量就多达百万。
蝉为了获取异性的注意会向着对方鸣叫。数量庞大的蝉只一起和鸣则会制造出极为宏大的噪音,以至于每过17年,当这种蝉进入活跃期时,当地居民往往会暂时搬离,以求耳根清净。鲍伯·迪伦便是因为1970年在普林斯顿大学攻读学位时听到周围森林里出现的刺耳蝉鸣,才写下他那首叫做《蝗虫岁月》的歌曲。
当这些蝉只成功吸引异性并完成交配后,每只雌蝉会在地面上产下大约600只卵。然后,经过6周的狂欢,所有蝉只寿终正寝,森林将重回长达17年的宁静。下一代的蝉卵在仲夏孵化,其幼虫坠落在森林地表,然后钻进泥土中,寻找到根茎以吸取养分。然后,经过又一个17年的轮回,下一场蝉的狂欢将重新上演。
这些蝉能感受到17年的时光流逝,绝对是让人不可思议的生物工程。几乎没有蝉只会提前一年或推迟一年出洞。多数动植物所遵循的年度生命周期都是受气温和季节的变化所影响的。那么这些蝉只每隔17个地球公转周期后现身一次,又是因为什么呢?人们对此并没有确切的解释。
对数学家来说,最令人好奇的一点就是这类蝉选择的数字17是一个质数。它们为什么要选择在地底下度过17年这个质数的周期呢,这仅仅是巧合吗?似乎并非如此。除了此类蝉以外,还有一些种类的蝉会在地下度过13年的时间,另外也有几种喜欢在地下生活7年。上述这些数字全是质数。而如果一只17年周期的蝉确实提早钻出地面,它不会只提早一年,而通常会提早4年,其生命周期也因此转变成13年,这一点颇为惊奇。似乎冥冥中果真有什么质数仙子在协助这些蝉只物种。然而,到底是什么在作祟呢?
科学家对此并没有给出明确的结论,到底蝉类为何青睐质数,这里有一个数学上的推测。首先讲明几点事实。一片森林中只能栖息一个种群的蝉只,因此该解释并不涉及不同种群共享一片森林的情况。在大部分年份中,总会有一种质数蝉种出现在美国某些地区。但是,2009年和2010年则是蝉类销声匿迹的年份。与此相反,2011年,数量庞大的13年周期的蝉种在美国东南部破土而出。(意外的是,2011本身刚好也是一个质数,但我并不认为蝉会聪明到这种程度。)
关于蝉的质数生命周期,迄今为止的最佳推测指出,森林中可能存在着一种蝉类的天敌,周期性地出现,而且其生命周期刚好对应蝉的出土时间,于是,它们便可饕餮不断涌现的美食了。接下来,物种的自然选择便开始发挥作用,保持质数生命周期的蝉类遭遇天敌的机会要远远小于非质数生命周期的蝉类。
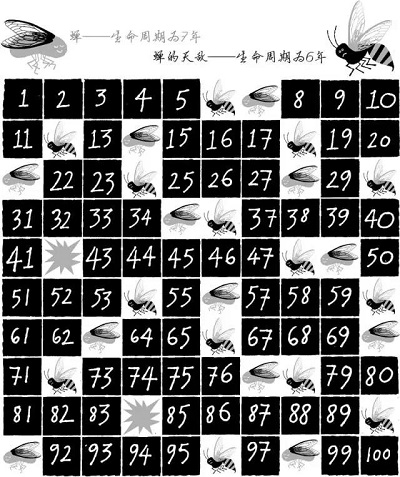
图1:100年内,生命周期为7年的蝉类和生命周期为6年的天敌的遭遇情况
举例来说,假设其天敌每6年出现一次。那么7年生命周期的蝉类则会每42年才遭遇一次该天敌。相反,如果某种蝉类的生命周期是8年,那么其遭遇该天敌的周期则是24年;而生命周期为9年的蝉类与天敌的遭遇机会则更多,每18年就有一次。
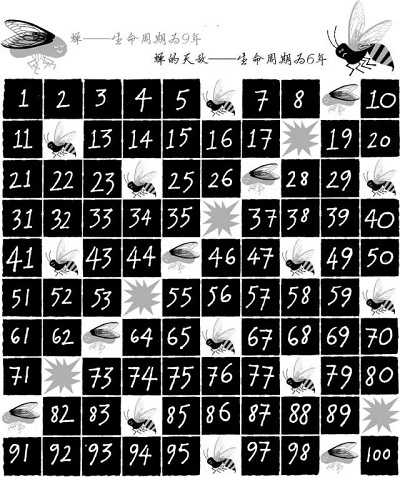
图2:100年内,生命周期为9年的蝉类和生命周期为6年的天敌的遭遇情况
在北美洲广阔的森林里面,究竟哪个物种占据了最大的一个质数,竞争似乎非常激烈。蝉类应对天敌的技巧非常娴熟,以至于其天敌要么饥饿而终,要么迁徙别处,只留下有着奇怪质数周期的蝉类独自狂欢。但我们接下来将要看到,蝉类并非世界上唯一一种利用质数作为切分节奏的生物。

图3

图4
注:文章摘自《神奇的数学:牛津教授给青少年的讲座》,好玩的数学整理发布。
声明:文章转自【好玩的数学】微信公众号,版权归原作者所有,转载仅供学习使用,不用于任何商业用途,如有侵权请联系删除,谢谢。











