下面是我们《马同学线性代数基础班》的节选。
矩阵、矩阵乘法最初的目的是为了解线性方程组。
在现实生活中有很多线性方程组，比如：
一、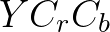
色彩空间
电视机成像的原理大概是，通过一把电子枪，把电子打到屏幕上：
图1
不过对于这样的彩色图片：
图2
根据之前我们对色彩空间的介绍，我们以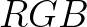
为基，可张成整个色彩空间。
所以，我们可以使用三把电子枪，分别是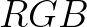
，来呈现出彩色的画面：
图3
但是，电视台那边过来的信号不是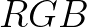
，而是
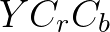，其中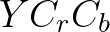
是对色彩空间的另外一种分解方式。
这点从我们电视背后的接口就可以看出，在下图中标注的色差接口，即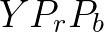
，其实就是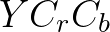
（两者的区别不是在色彩分解上，而是电视成像技术中的“逐行扫描”以及“隔行扫描”。也有资料说，一个是数字信号，一个是模拟信号，仅供参考）：
图4
下面是之前彩图的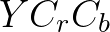
分解，第二幅图就是灰度图，也就是
：
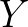图5
这是有原因的，因为最早的电视是黑白电视，升级到彩色电视，但是依然要保持对黑白电视的兼容，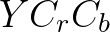
中的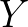
正好是灰度图，可以让黑白电视成像。
假如你是黑白电视，背后应该就只有一个视频输入接口，只需插入电视台过来的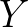
信号就可以观看了。
但是，如果是彩色电视，那么得到电视台传过来的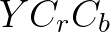
信号，就需要解如下方程组得到
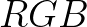，给三把电子枪使用：
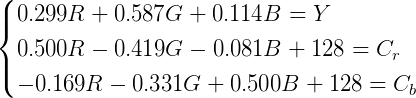
这个方程组怎么解呢？
二、高斯消元法
已知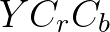
求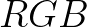
实际是一个线性方程组，解这种方程组有一个通用的办法，高斯消元法。
1. 高斯消元法的目标
之前的方程不好计算了，我们举一个简单的例子：
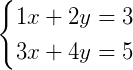
从几何上来讲，两个方程都是直线，求解方程组就是找到两根直线的交点：
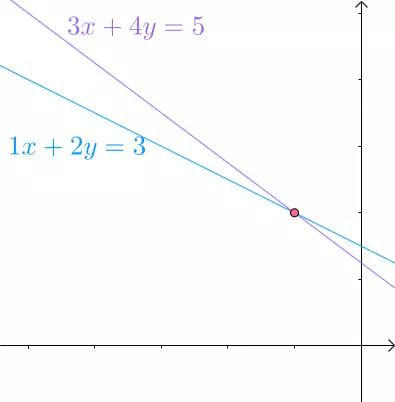
图6
因为都是直线，所以我们称为线性方程组。
求解的思路几乎是句废话，即找到交点的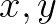
坐标：
图7
也就是把方程化成这个样子：
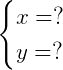
这就是高斯消元法的目标。
2. 高斯消元法的思路
要达到这个目标，高斯消元法的思路是，第一行把这些给消了：
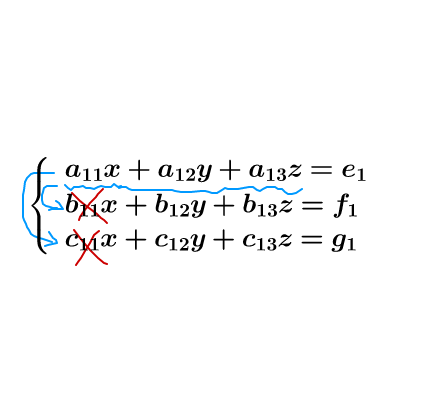
图8
第二行把这些给消了：
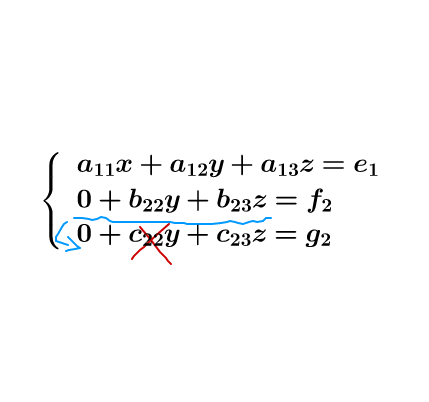
图9
第三行反过来，把这些给消了：
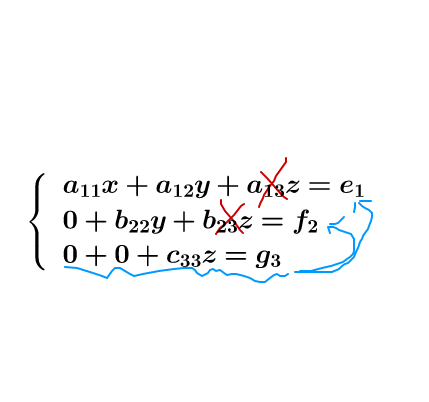
图10
第二行，把这些给消了：
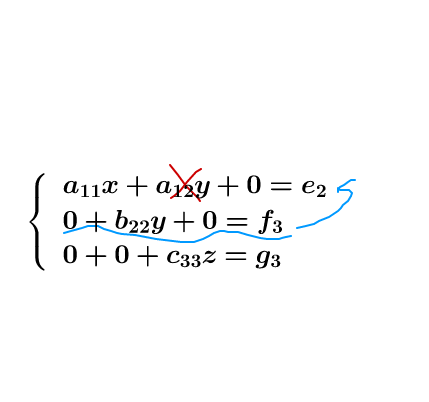
图11
最后，达到目标：
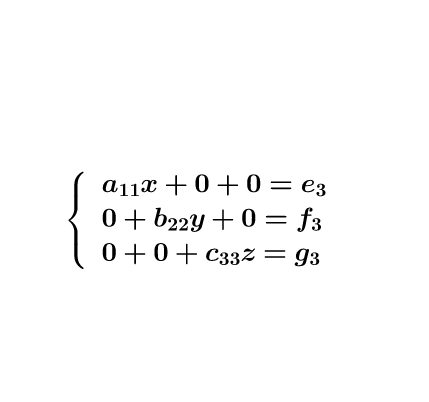
图12
3. 例子
下面我们看看怎么用高斯消元法来解。
先标注一下方程组，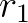
表示第一行，
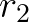表示第二行：
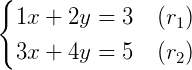
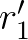表示新的第一行，
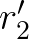表示新的第二行，我们进行以下操作：
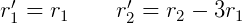
其中，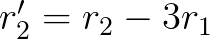
的意思就是：
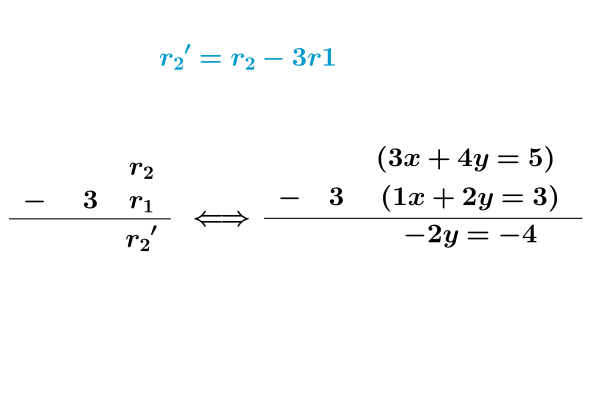
图13
我们得到新的方程组：
按照这个思路，完整的解题过程如下：
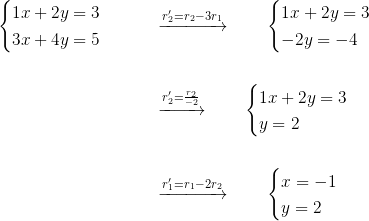
至此，解出答案：
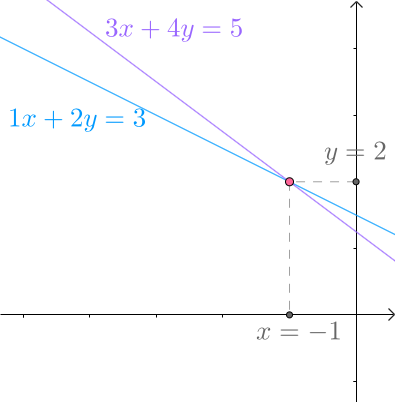
图14
三、标记法
图15
英国数学家阿瑟·凯莱(1821-1895)对于看似简单的高斯消元法进行了研究，得出了惊人的结果。
他当时研究矩阵的动机出于对线性方程组计算的简化。
比如，下面是一个线性方程组：
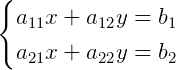
对于这样一个线性方程组，在固定未知数的顺序（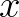
出现在第一个位置，
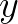出现在第二个位置，常数在等号右边）后，且保证每个未知数都出现(不出现时，系数为0)，方程组就只需要系数来表示了。
按照上面的规定，方程组可以简写为如下数块：
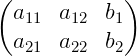
1. 练习题
:将
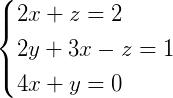
用数块来表示。
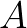:在保证顺序且每个未知数都出现的原则下，原方程组可改写为：
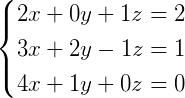
因此，方程组写成数块形式为：
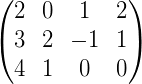
四、凯莱的高斯消元法
我们开始用凯莱的方法进行高斯消元法。
1. 方程简化
还是解之前的方程组：
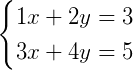
将方程组简化为数块：
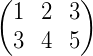
之前说过，高斯消元法的目标是：
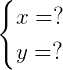
写完整点就是：
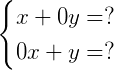
因此我们的目标就是要把数块变成下面这个样子：
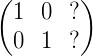
对应之前的高斯消元法：
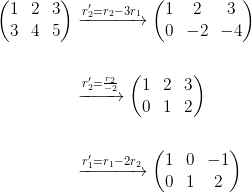
得到结果：
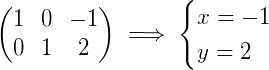
正如你看到的，解起来并不复杂，但是要将过程描述清楚却很繁琐，这很不数学。
能不能更优雅的展现这个过程呢？
2. 数块乘法
数学家发明了一种数块的乘法，简洁地进行高斯消元法。
(1) 单行乘法
将
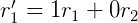
定义为:
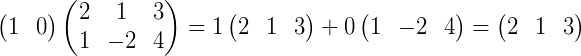
(2) 多行乘法
对于：
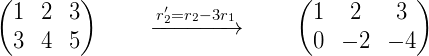
它表达了两个过程：
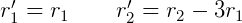
将此定义为：
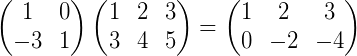
其中第一行运算的结果放在第一行，第二行运算的结果放在第二行：
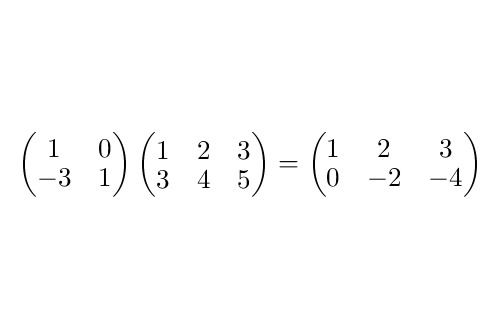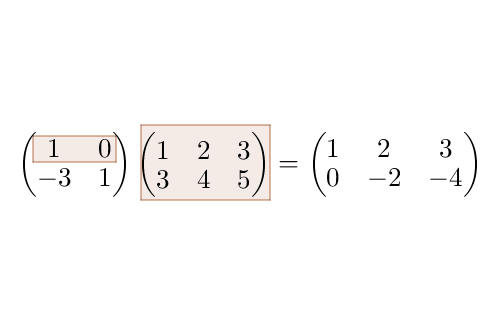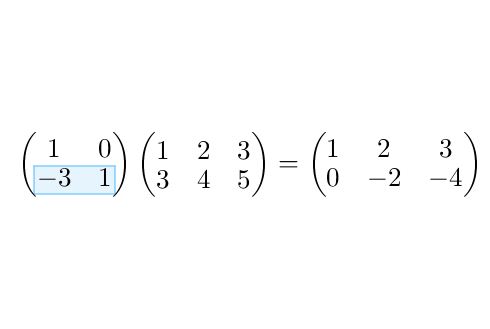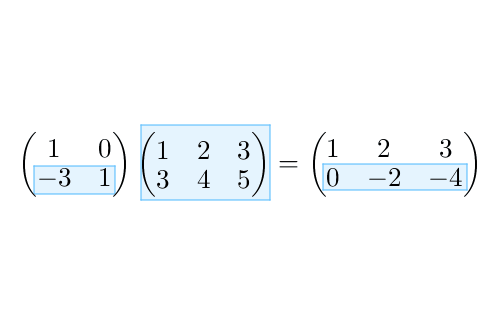
图16
3. 过程简化
有了这个运算规则后，整个高斯消元法就可以表示如下：
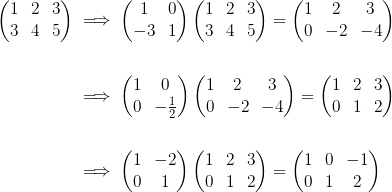
至此，得到答案：
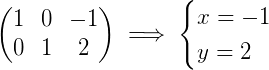
可见，数块以及对应的乘法，在高斯消元法的过程中，非常简洁清楚易用。
五、矩阵的定义
阿瑟·凯莱在1858年的《矩阵理论纪要》的论文中，给这个数块以合法的数学地位，取了一个名字：矩阵。刚才的数块乘法自然也被称为了矩阵乘法。
声明：文章转自【马同学高等数学】微信公众号，版权归原作者所有，转载仅供学习使用，不用于任何商业用途，如有侵权请联系删除，谢谢。
